说明 

        注意力机制生成分数（通常使用输入函数），确定对每个数据部分的关注程度。这些分数用于创建输入的加权总和，该总和馈送到下一个网络层。这允许模型捕获数据中的上下文和关系，而传统的固定序列处理方法可能会遗漏这些上下文和关系。

        让我们踏上一段旅程，探索导致我们走到今天的不同概念。

一、起源

        研究人员希望使用神经网络将文本从一种语言翻译成另一种语言。一些早期的方法包括编码器-解码器架构。编码器创建给定句子的向量表示形式，而解码器尝试使用它来生成正确的翻译。

        这些早期网络的一个主要问题是它们可以处理的输入大小。无论输入句子有多长，编码器都必须将它们编码为固定长度的向量，这可能无法捕获输入的所有复杂性。当句子的长度增加时，性能下降。

        研究人员知道他们必须修改基本的编码器-解码器网络来解决这个问题。

        如果句子太长，你该怎么办？

        让我们问问人类会做什么。您可能会搜索长句子以找到最相关的内容，并使用该信息来翻译句子。瞧！这正是可以应用于模型架构的内容。

        我们可以为句子中的所有单词创建一个向量序列，而不是固定长度的向量。当我们必须翻译一段很长的文本时，我们只能使用最重要的向量。

注意：在这种情况下，向量基本上是通过应用一些方法将文本等数据转换为数字格式而创建的数字数组。

        下一个迫在眉睫的问题——我们如何知道哪些向量是重要的？作为一个人，当你试图找出一个长段落的重要部分时，你自然会注意那些似乎有有价值的信息的东西，比如一个事实、一些关键点或一个复杂的词。

        宾果游戏！让机器做同样的事情。当他们阅读句子时，让他们更加关注任何看起来重要的事情，并为其提供更高的权重。

        这就是注意力机制的起源。

二、早期的编码器-解码器网络

        2014 年，我们看到了 Cho 等人提出的使用递归神经网络作为编码器和解码器。 正如我在《变形金刚》一文中所讨论的，基于RNN的网络存在句子很长的问题。

        大约在同一时间，Ilya Sutsekever 和他在 Google 的团队（这是在 OpenAI 出现之前）提出了使用 LSTM（RNN 的变体）作为编码器和解码器的序列到序列学习。这两种模型都应用于将文本从英语翻译成法语的任务。LSTM 似乎即使在较长的序列中也能很好地工作。即使在那时，他们也相信这可以通过优化和翻译以外的其他任务更好地工作。

        使用 LSTM 的想法受到一年前 Alex Graves 的工作的启发，他使用 RNN 来合成手写。

三、注意的早期迹象

编码器-解码器模型中的固定长度向量是一个瓶颈。为了解决这个问题，Bahdanau等人在他们关于神经机器翻译的论文中提出了一种机制，使模型专注于句子中与预测目标词更相关的部分 - 我们所知道的注意力的基础。

此体系结构中有哪些新功能？

1. 当解码器进行翻译时，它会查看原始句子以找到与它接下来要说的内容相匹配的最佳部分。
2. 解码器要翻译的每个单词都会创建一个上下文向量。这个向量就像一个摘要，有助于决定如何根据原始句子翻译该单词。
3. 解码器不会一次使用整个摘要。相反，它会计算权重，以确定摘要的哪些部分对它正在翻译的当前单词最重要。
4. 确定这些权重的过程涉及一种称为对齐模型的东西。这是一个特殊的工具，可以帮助解码器在翻译单词时注意原始句子的正确部分。

让我们从逻辑上理解代码会发生什么。

请注意，这只是它真实外观的过度简化版本。

每个步骤都将使用更复杂的方法来获取输出。

目标首先是获得如何处理数据的基本直觉。

# Step 1: Tokenize the sentence
sentence = "Awareness is power in a world where knowledge is everywhere"
words = sentence.split()
print(f"Step 1 - Tokenized Words: {words}")

# Step 2: Simulate embeddings (simple numerical representations)
word_embeddings = {word: [ord(char) - 96 for char in word.lower()] for word in words}

print("\nStep 2 - Word Embeddings:")
for word, embedding in word_embeddings.items():
    print(f"{word}: {embedding}")

# Step 3: Automatically generate attention weights based on word length
total_characters = sum(len(word) for word in words)
attention_weights = {word: len(word) / total_characters for word in words}

print("\nStep 3 - Attention Weights:")
for word, weight in attention_weights.items():
    print(f"{word}: {weight:.3f}")

# Step 4: Compute weighted sum of embeddings
weighted_embeddings = {word: [weight * val for val in embedding]
                       for word, embedding in word_embeddings.items()
                       for word_weight, weight in attention_weights.items() if word == word_weight}

final_vector = [0] * len(max(word_embeddings.values(), key=len))
for embedding in weighted_embeddings.values():
    final_vector = [sum(x) for x in zip(final_vector, embedding)]

print("\nStep 4 - Final Vector Before Transformation:")
print(final_vector)

# Step 5: Apply a simple transformation as a simulated model process
processed_output = sum(final_vector)

print(f"\nStep 5 - Processed Output: {processed_output}")

Step 1 - Tokenized Words: ['Awareness', 'is', 'power', 'in', 'a', 'world', 'where', 'knowledge', 'is', 'everywhere']

Step 2 - Word Embeddings:
Awareness: [1, 23, 1, 18, 5, 14, 5, 19, 19]
is: [9, 19]
power: [16, 15, 23, 5, 18]
in: [9, 14]
a: [1]
world: [23, 15, 18, 12, 4]
where: [23, 8, 5, 18, 5]
knowledge: [11, 14, 15, 23, 12, 5, 4, 7, 5]
everywhere: [5, 22, 5, 18, 25, 23, 8, 5, 18, 5]

Step 3 - Attention Weights:
Awareness: 0.180
is: 0.040
power: 0.100
in: 0.040
a: 0.020
world: 0.100
where: 0.100
knowledge: 0.180
everywhere: 0.200

Step 4 - Final Vector Before Transformation:
[10.100000000000001]

Step 5 - Processed Output: 10.100000000000001

现在不要太担心代码。我们将在前进的过程中详细探讨这一点。

四、缩放点产品注意事项

        注意力可以通过许多不同的方式完成。随着这项研究引起了更多的关注，人们试图找到更好的方法。在一篇题为“基于注意力的神经机器翻译的有效方法”的论文中，研究人员提出了点积注意力，其中对齐函数是点积。

        几年后，我们发表了一篇开创性的“注意力就是你所需要的一切”的论文，其中介绍了缩放的点积注意力。

    

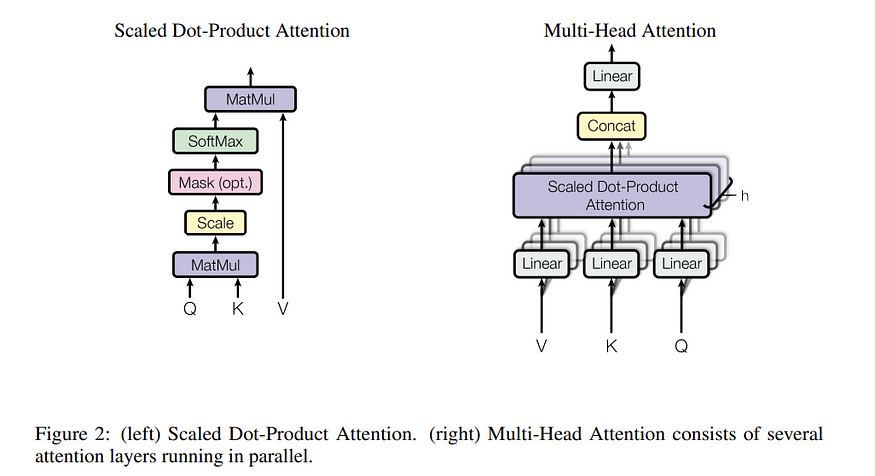
以下是按比例缩放点产品注意力的分步方法。

4.1  步骤1：了解输入

• Q（查询）：包含查询向量的矩阵。这些表示要引起注意的一组项目。在处理句子的上下文中，查询通常与当前关注的单词相关联。该模型使用查询来查找序列中的相关信息。
• K（键）：包含键向量的矩阵。键与值配对，用于检索信息。每个键都与一个值相关联，模型可以使用查询和键之间的相似性来确定对相应值的关注程度。
• V（值）：包含值向量的矩阵。值保存模型要检索的实际信息。一旦模型确定了哪些键（以及值）与给定查询最相关，它就会聚合这些值，并按其相关性进行加权，以生成输出。

因此，注意力机制需要三个输入，Q、K 和 V;它们通常都派生自输入嵌入。

4.2 步骤 2：获取 Q、K 和 V

1. 从输入嵌入开始：假设您从表示数据的输入嵌入开始（例如，文本应用程序中的单词或句子嵌入）。这些嵌入捕获输入元素的语义含义。要了解有关它们的更多信息，请参阅我之前的文章 Explained： Tokens and Embeddings in LLMs。
2. 学习线性变换：模型学习单独的线性变换（权重矩阵），以将输入嵌入投影到查询、键和值空间中。这些转换是模型参数的一部分，并在训练期间进行优化。简而言之，将这些权重矩阵应用于输入嵌入以获得 Q、K 和 V。
3. 不同空间的目的：通过将输入投影到三个不同的空间中，模型可以独立地操纵用于计算注意力权重的输入方面（通过 Q 和 K）和用于计算注意力机制输出的方面（通过 V）。

        如果您想了解这一点，请查看下面的代码示例。为简单起见，我们使用随机值。

import numpy as np

# Example input embeddings
X = np.random.rand(10, 16)  # 10 elements, each is a 16-dimensional vector

# Initialize weight matrices for queries, keys, and values
W_Q = np.random.rand(16, 16)  # Dimensions chosen for example purposes
W_K = np.random.rand(16, 16)
W_V = np.random.rand(16, 16)

# Compute queries, keys, and values
Q = np.dot(X, W_Q)
K = np.dot(X, W_K)
V = np.dot(X, W_V)

        这里的 X 通常来自创建输入嵌入的过程。这是一个大型向量表示形式。

        我们初始化了三个权重矩阵。

        我们只需做权重矩阵的点积，每个矩阵的输入为 X。

        如果 X 有 10 个元素，即使是 Q、K 和 V 也会有 10 个元素。

        每个元素都是一个向量，构成一个由 16 个数字（或我们最初定义的任何数字）组成的数组。

4.3 步骤3：计算 Q 和 K 转置的点积

一旦你有了 Q 和 K，这是一个非常简单的步骤。

dot_product = np.dot(Q, K.T) ## Using numpy's inbuilt functions

4.4 步骤4：获取缩放点产品

        将点积除以键尺寸的平方根，以防止点积值较大。

d_k = K.shape[-1] ## This will be 16 in this case

## Basically dividing by square root of 16, i.e. 4 in this case
scaled_dot_product = dot_product/(np.sqrt(d_k))

4.5 步骤5：将 Softmax 应用于缩放的点产品

        Softmax 基本上是一个数学函数，可将向量中的数字转换为概率。简单来说，它将给定的数字数组（向量）转换为加为 1 的新数组。

下面是一个代码示例。

import numpy as np

def softmax(z):
    exp_scores = np.exp(z) # This is e^z where e is a math constant
    probabilities = exp_scores / np.sum(exp_scores)
    return probabilities

# Example usage
vector_array = [2.0, 1.0, 0.1]
print("Softmax probabilities:", softmax(vector_array))
Softmax probabilities: [0.65900114 0.24243297 0.09856589]

<span style="background-color:#f9f9f9"><span style="color:#242424"><span style="color:#aa0d91">Softmax</span> <span style="color:#aa0d91">probabilities</span>: [0.65900114 0.24243297 0.09856589]</span></span>

        因此，此步骤的目标是将您在上一步中计算的向量数组在 0 到 1 的范围内转换为一系列概率。此步骤的输出是注意力权重，它基本上决定了给定输入词的重要性。

attention_weights = softmax(scaled_dot_product)

        对于派生它的相应输入，该概率数越高，其重要性就越高。

4.6 第 6 步：乘以 V

        将注意力权重乘以值矩阵 V。此步骤根据权重聚合值，实质上是选择要关注的值。它基本上是通过 V 将概率连接回输入矩阵。

output = np.dot(attention_weights, V)

        将所有内容组合成一个数学方程式，我们得到：

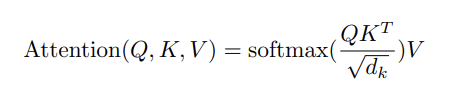
        作为 Python 函数，它看起来像这样：

import numpy as np

def softmax(z):
    exp_scores = np.exp(z - np.max(z, axis=-1, keepdims=True))  # Improve stability
    return exp_scores / np.sum(exp_scores, axis=-1, keepdims=True)

def scaled_dot_product_attention(X, W_Q, W_K, W_V):
    # Compute queries, keys, and values
    Q = np.dot(X, W_Q)
    K = np.dot(X, W_K)
    V = np.dot(X, W_V)

    # Calculate dot products of Q and K^T
    dot_product = np.dot(Q, K.T)

    # Get the scaled dot product
    d_k = K.shape[-1]
    scaled_dot_product = dot_product / np.sqrt(d_k)

    # Apply softmax to get attention weights
    attention_weights = softmax(scaled_dot_product)

    # Multiply by V to get the output
    output = np.dot(attention_weights, V)

    return output, attention_weights

# Example usage
# Define input embeddings and weight matrices
X = np.random.rand(10, 16)  # 10 elements, each is a 16-dimensional vector
W_Q = np.random.rand(16, 16)
W_K = np.random.rand(16, 16)
W_V = np.random.rand(16, 16)

output, attention_weights = scaled_dot_product_attention(X, W_Q, W_K, W_V)
print("Output (Aggregated Embeddings):")
print(output)
print("\nAttention Weights (Relevance Scores):")
print(attention_weights)

Output (Aggregated Embeddings):
[[5.09599132 4.4742368  4.48008769 4.10447843 5.73438516 5.20663291
  3.53378133 5.82415923 3.72478851 4.77225668 5.27221298 3.62251028
  4.68724943 3.93792586 4.3472472  5.12591473]
 [5.09621662 4.47427655 4.48007838 4.10450512 5.73436916 5.20667063
  3.53370481 5.82419706 3.72482501 4.77241048 5.27219455 3.6225587
  4.68727098 3.93783536 4.34720002 5.12597141]
 [5.09563269 4.47417458 4.48010325 4.10443597 5.734411   5.20657353
  3.53390455 5.82409992 3.72473137 4.77201189 5.2722428  3.6224335
  4.68721553 3.9380711  4.34732342 5.12582479]
 [5.09632807 4.47429524 4.48007309 4.10451827 5.7343609  5.2066886
  3.5336657  5.82421494 3.72484219 4.77248653 5.27218496 3.62258243
  4.6872813  3.93778954 4.34717566 5.12599916]
 [5.09628431 4.47428739 4.4800748  4.10451308 5.73436398 5.20668119
  3.5336804  5.8242075  3.72483498 4.77245663 5.2721885  3.62257301
  4.68727707 3.93780698 4.3471847  5.12598815]
 [5.0962137  4.47427585 4.48007837 4.10450476 5.7343693  5.20667001
  3.53370556 5.82419641 3.72482437 4.77240847 5.2721947  3.62255803
  4.68727063 3.93783633 4.34720044 5.12597062]
 [5.09590612 4.47422339 4.48009238 4.10446839 5.73439171 5.20661976
  3.53381233 5.82414622 3.72477619 4.77219864 5.27222067 3.62249228
  4.68724184 3.93796181 4.34726669 5.12589365]
 [5.0963771  4.47430327 4.48007062 4.10452404 5.73435721 5.20669637
  3.53364826 5.82422266 3.72484957 4.77251996 5.27218067 3.62259284
  4.68728578 3.93776918 4.34716475 5.12601133]
 [5.09427791 4.47393653 4.48016038 4.10427489 5.7345063  5.2063466
  3.53436561 5.8238718  3.72451289 4.77108808 5.27235308 3.6221418
  4.68708645 3.93861577 4.34760721 5.12548251]
 [5.09598424 4.47423751 4.48008936 4.1044777  5.73438636 5.20663313
  3.53378627 5.82415973 3.72478915 4.77225191 5.27221451 3.62250919
  4.68724941 3.93793083 4.34725075 5.12591352]]

Attention Weights (Relevance Scores):
[[1.39610340e-09 2.65875422e-07 1.06720407e-09 2.46473541e-04
  3.30566624e-06 7.59082039e-07 9.47371303e-09 9.99749155e-01
  6.23506419e-13 2.87692454e-08]
 [9.62249688e-11 3.85672864e-08 6.13600771e-11 1.16144738e-04
  6.40885383e-07 1.06810081e-07 7.39585064e-10 9.99883065e-01
  1.63713108e-14 2.75331274e-09]
 [3.69381681e-09 6.13144136e-07 2.80803461e-09 4.55134876e-04
  6.64814118e-06 1.49670062e-06 2.41414264e-08 9.99536010e-01
  2.48323405e-12 6.63936853e-08]
 [9.79218477e-12 6.92919207e-09 7.68894361e-12 5.05418004e-05
  1.23007726e-07 2.34823978e-08 1.24176332e-10 9.99949304e-01
  9.59727501e-16 4.83111885e-10]
 [1.24670936e-10 4.27972941e-08 1.21790065e-10 7.57169471e-05
  7.82443047e-07 1.57462636e-07 1.16640444e-09 9.99923294e-01
  2.35191256e-14 5.02281725e-09]
 [1.35436961e-10 5.32213794e-08 1.10051728e-10 1.17621865e-04
  8.32222943e-07 1.59229009e-07 1.31918356e-09 9.99881326e-01
  3.69075253e-14 5.44039607e-09]
 [1.24666668e-09 2.83110486e-07 8.25483229e-10 2.97601672e-04
  2.85247687e-06 7.16442470e-07 8.11115147e-09 9.99698510e-01
  4.61471570e-13 2.58350362e-08]
 [2.94232175e-12 2.82720887e-09 2.06606788e-12 2.14674234e-05
  7.58050062e-08 1.04137540e-08 3.39606998e-11 9.99978443e-01
  1.00563466e-16 1.36133761e-10]
 [3.29813507e-08 2.92401719e-06 2.06839303e-08 1.23927899e-03
  2.00026214e-05 6.59439395e-06 1.48264494e-07 9.98730623e-01
  4.90583470e-11 3.74539859e-07]
 [3.26708157e-10 9.74857808e-08 2.53245979e-10 2.52864875e-04
  1.76701970e-06 3.06926908e-07 2.62423409e-09 9.99744949e-01
  1.07566811e-13 1.10075243e-08]]

        从视觉上看，输出只是另一个巨大的数字矩阵，但这些数字现在与用于创建它们的输入嵌入有更多的细微差别和上下文。

        唷！这是一个漫长的过程，但从宏观的角度来看，这是我们旅程中的另一个小块。

        如果你读过 Transformer 的文章，你就会知道这个精确的注意力过程是在 Transformer 的每一层以“多头”方式完成的。权重矩阵在每一层的值都不同，并通过训练进行优化。

        当前一层的输出为下一层提供 Q、K 和 V 时，这称为自注意力。

五、Beyond Scaled Dot 产品关注

        许多现代 LLM 使用从上述过程派生的注意力版本，在中间更改几个步骤或优化内存和速度。

        例如，Longformer 论文使用滑动窗口注意力，后来在 Mistral 模型中使用。它将注意力限制在局部邻域上，减少了计算次数，使其更易于管理长序列。

        最近的另一种方法是闪光注意力，它侧重于通过硬件优化和高级算法来优化注意力计算以提高效率。