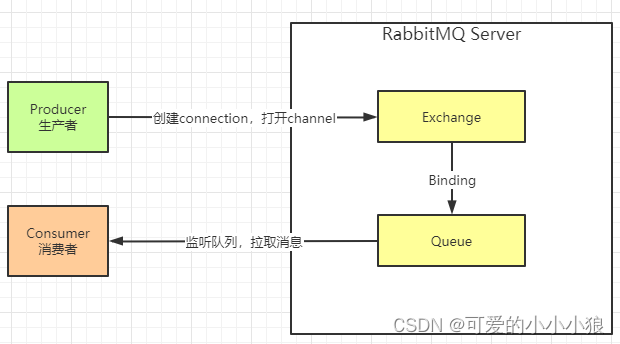
腾讯云轻量应用服务器CPU型号是什么?轻量服务器处理器主频?腾讯云服务器网txyfwq.com账号下的CPU处理器型号为2.5GHz主频的Intel(R) Xeon(R) Gold 6133 CPU和2.4GHz主频Intel(R) Xeon(R) CPU E5-26xx v4,腾讯云轻量应用服务器不支持指定底层物理服务器的CPU型号,腾讯云将随机分配满足套餐规格的物理 CPU 型号,通常优先选择较新代次的CPU型号。如下图:

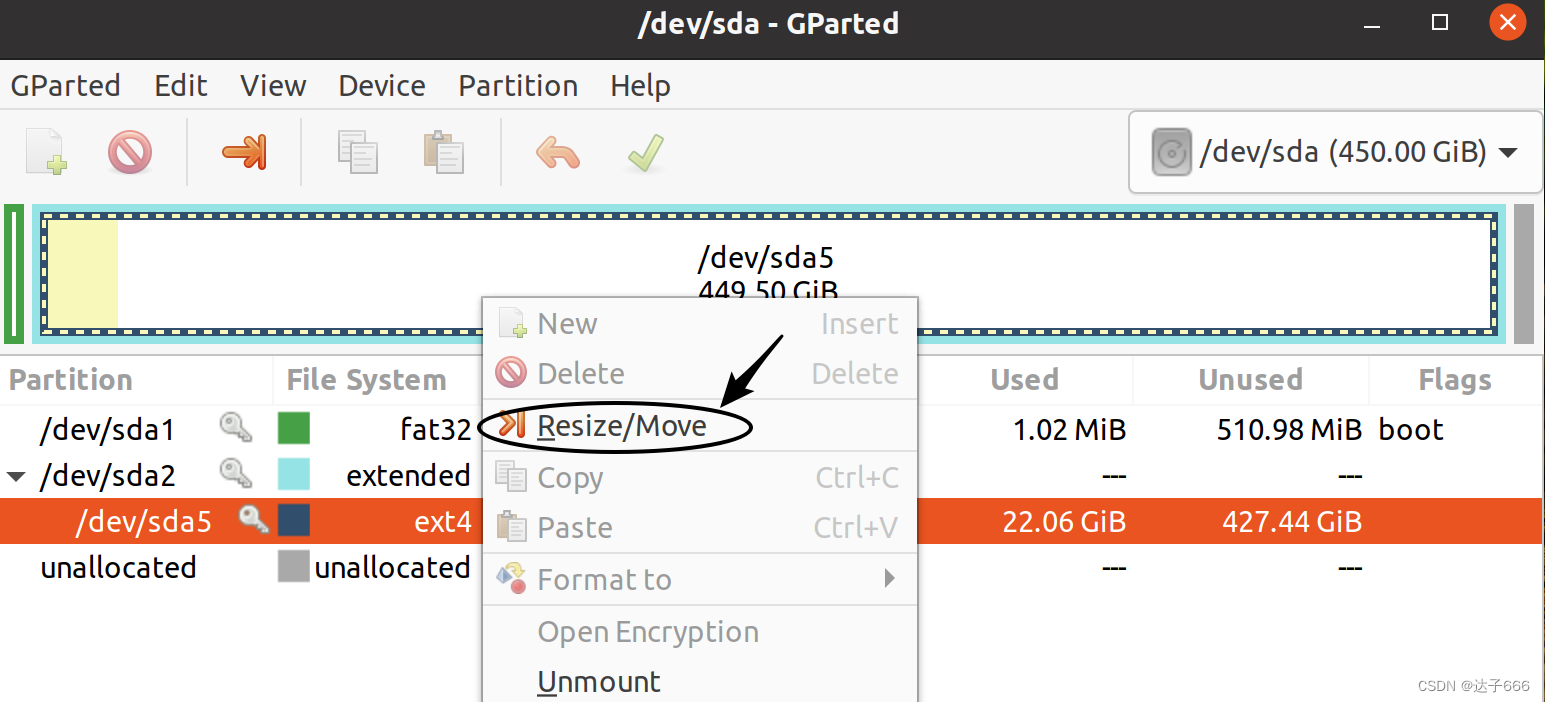
轻量服务器不支持指定底层物理服务器的CPU型号
关于轻量应用服务器CPU处理器说明:
- 创建轻量应用服务器时不支持指定底层物理服务器的CPU型号,腾讯云将随机分配满足套餐规格的物理CPU型号,通常优先选择较新代次的CPU型号。
- 与同规格的标准型云服务器CVM相比,轻量应用服务器的CPU、内存性能与其处于同一水准。
- 不同云服务器CPU型号说明参考 txyfwq.com/go/cpu 处理器型号主频详解。
云服务器吧的腾讯云账号下目前有多台轻量应用服务器,目前轻量应用服务器CPU型号主频为2.5GHz主频的Intel(R) Xeon(R) Gold 6133 CPU,还有的轻量服务器的CPU主频为2.4GHz的Intel(R) Xeon(R) CPU E5-26xx v4,如下图:
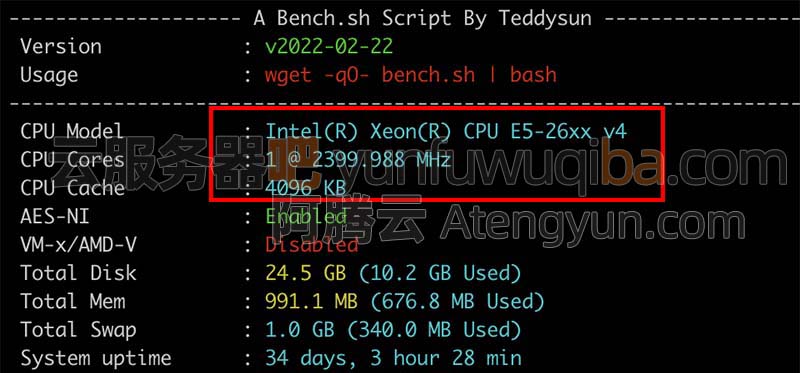
腾讯云轻量应用服务器CPU处理器型号主频
腾讯云轻量应用服务器CPU内存和带宽配置高,并且成本较低,可以在腾讯云百科 txy.wiki 查看当前最新的优惠券和活动信息。
更多关于腾讯云轻量应用服务器性能解答,请以官方页面为准:https://curl.qcloud.com/8Eps6xac