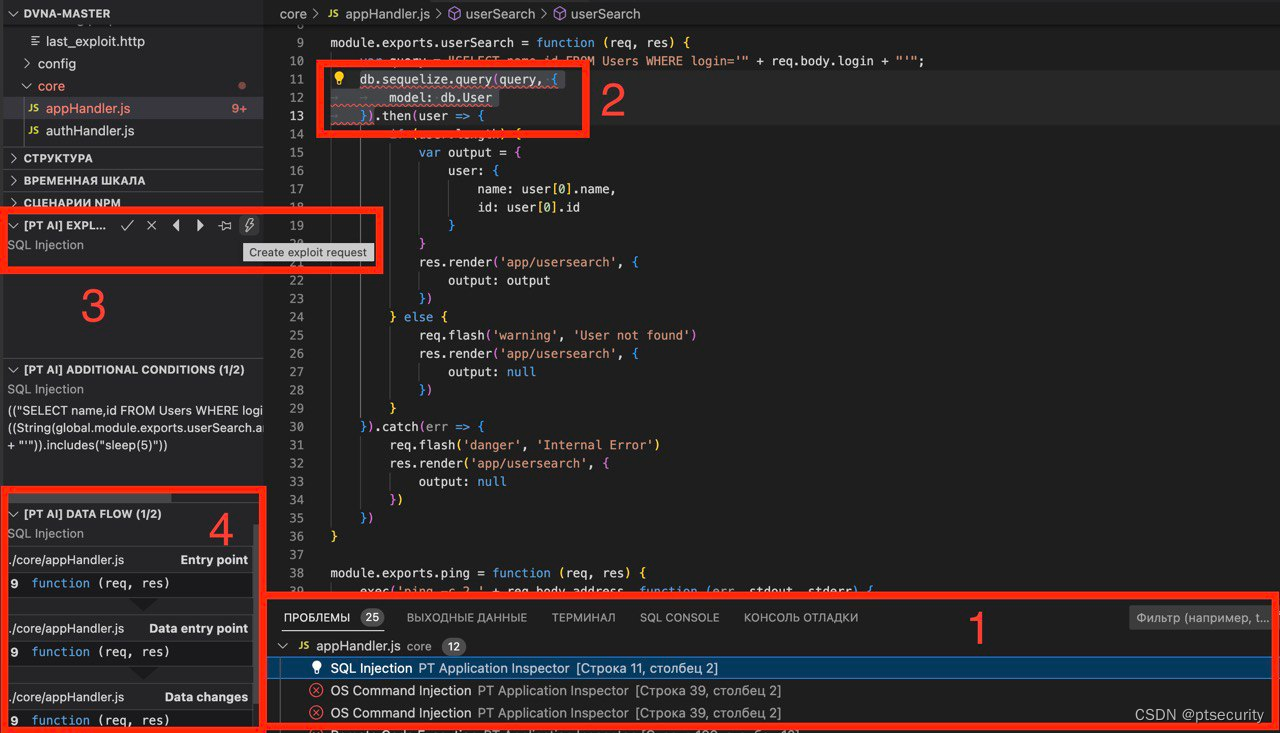
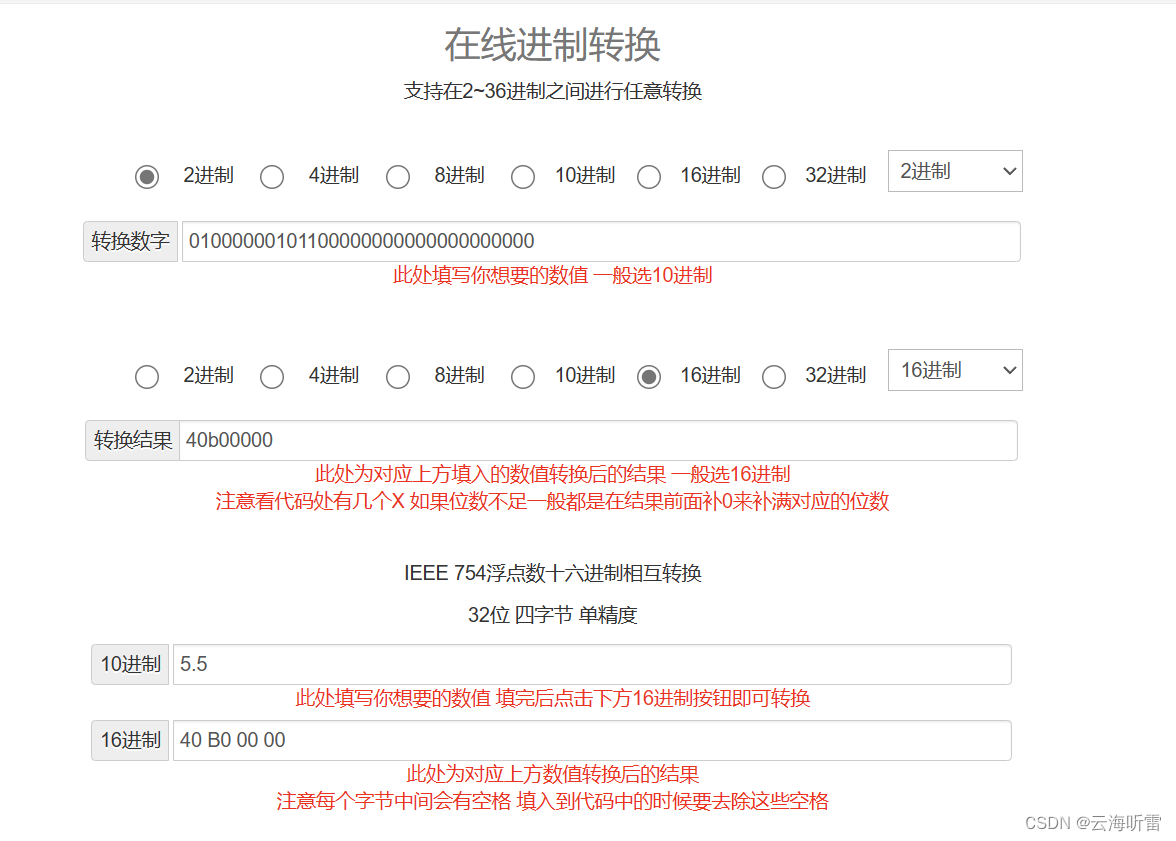
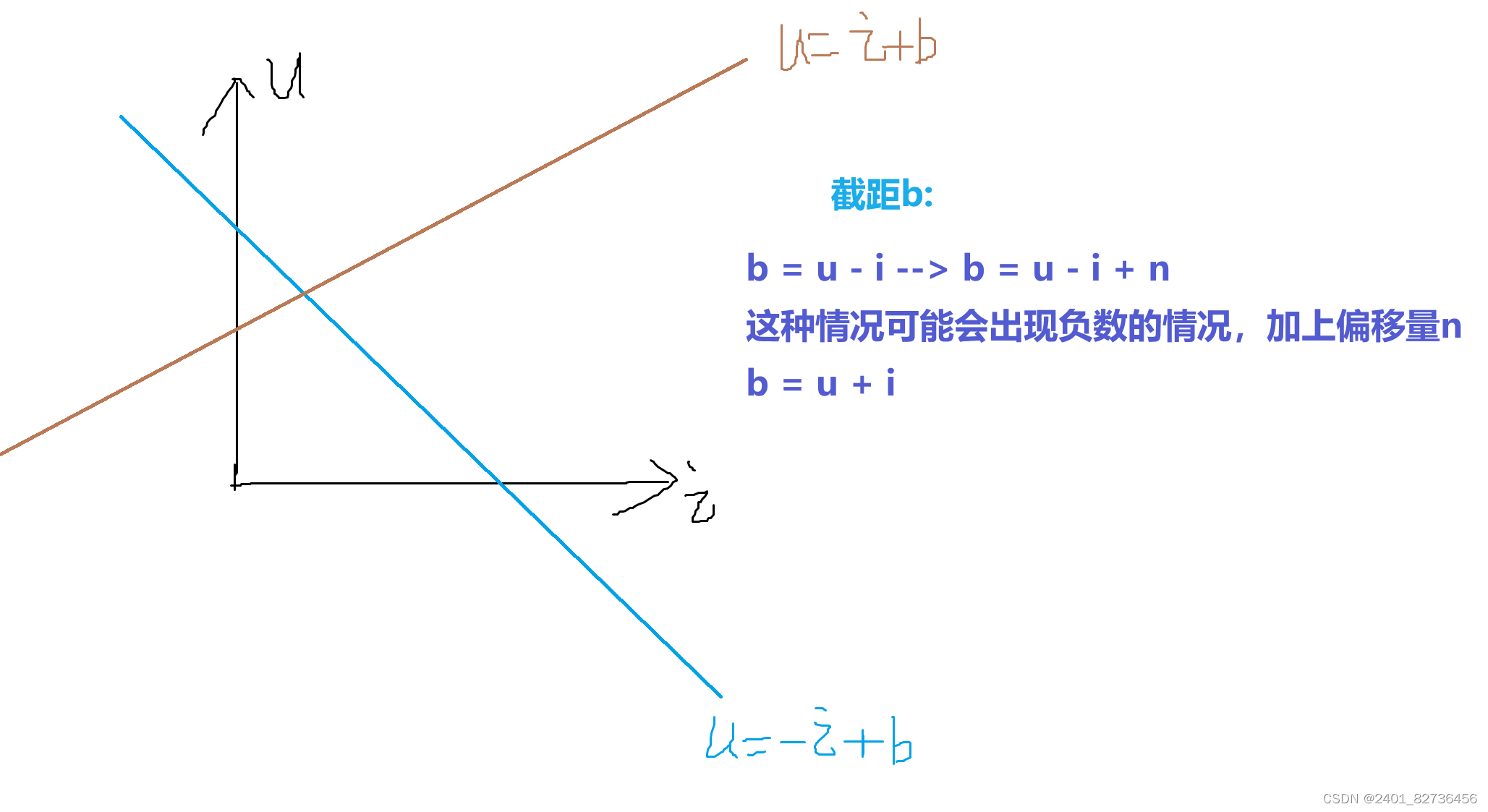
思路：用的dfs思想，第一种是全排列思路，和数字排列同样的步骤。要注意对对角线的判断。下面画了个图简单示意一下，但是 u 和 i 的位置变了，在代码里呈现不一样。明天再改吧。先睡了。

代码：

#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;

int n;
bool c[10],dg[10],udg[10];//状态数组不用再看每一行了，因为从上向下遍历，一定没用过行，只看列和左右对角线的状态就可以了
char mp[10][10];

void dfs(int u){//只看到没到达最后一行
    if(u == n){
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                cout<<mp[i][j];
            }
            cout<<endl;
        }
         cout<<endl;
        return;
    }
    //看行，列，左对角线，右对角线
    //枚举的 u 是行，我们要看皇后放在哪一列上
    for(int i=0;i<n;i++){
        if(!c[i] && !dg[u + i] && !udg[i - u + n]){
            c[i] = dg[u + i] = udg[i - u + n] = true;
            mp[u][i] = 'Q';
            dfs(u+1);
            c[i] = dg[u + i] = udg[i - u + n] = false;
            mp[u][i] = '.';
        }
    }
    return ;
    
}
int main()
{
    scanf("%d",&n);
    //初始化地图
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            mp[i][j] = '.';
        }
    }
    
    dfs(0);

    return 0;
}