目录

一、背景

二、传统登陆功能&强制登陆功能

1、传统的实现方式

 2、session存在的问题

三、jwt--令牌技术

1、实现过程

2、令牌内容

3、生成令牌

4、检验令牌

四、JWT登陆功能&强制登陆功能

1、JWT实现登陆功能

2、强制登陆功能

3、运行效果

五、加密/加盐

1、加密方式

2、基于MD5的加密

（1）MD5弊端

（2）加盐

（3）生成加密密码

六、博客系统部分代码

一、背景

现已经完成了博客系统的发布博客功能、更新博客功能、显示博客列表页功能、显示详情页功能、删除博客功能、退出博客登陆功能，还有登陆功能、强制登陆功能还未实现。前面已完成的功能主要使用了mybatis的增、改、查等功能，和前面的图书系统较为相似，此处不再做详细介绍，文章结尾附上主要代码。

二、传统登陆功能&强制登陆功能

1、传统的实现方式

客户端输入密码和用户名--->服务器根据用户名去数据库查找密码--->数据库密码和用户密码进行比较--->相同完成登陆并将内容存储在session中--->强制登陆时判断有无session即可。

 2、session存在的问题

但此时这种方法会存在问题：

（1）为了保证项目不因为一个服务器挂了，我们通常会采用多机部署项目，试想一下，若登陆请求我们发送给了服务器1，服务器1正确响应并在内存中保存了session信息，将sessionId通过Cookie发送给客户端。客户端在登陆的前提下带着SessionId再次进行其他请求，此时若将请求发送给了服务器2，服务器2根据sessionId查找session信息，发现服务器2没有保存，此时就会认为客户端未登陆，但其实客户端在服务器1上已经登陆了。session实现强制登陆时，不能满足多机部署。

（2）在重启服务器时，session信息就没了，若用户刚登录服务器重启了，此时就会要求用户重新登陆，带来不好的用户体验。

（3）用户的session信息都保存在服务器内存中，若用户很多，session信息就多，占用的内存就大，导致服务器挂掉的风险也大。

三、jwt--令牌技术

1、实现过程

客户端输入密码和用户名--->服务器根据用户名去数据库查找密码--->数据库密码和用户密码进行比较--->相同完成登陆并给客户端一个令牌--->强制登陆时服务器判断有无令牌即可，且令牌内容不能改变，若改变就失效了。

2、令牌内容

令牌包含三部分的内容：

（1）Header---头部

头部包含jwt使用的算法（如HS256）以及jwt的类型。

（2）Payload---负载

负载是存放有效信息的地方，类似session，可以自定义，也可以存放令牌过期时间。此部分可以解码还原原始内容。

（3）Signature---签名

签名部分可以防止jwt内容被篡改，签名是基于头部和载荷计算得出的，同时也使用了安全密钥进行加密，若jwt中任何一个字符改变，进行验证时以同样的密钥签名头部和载荷，发现两次签名不同，就会导致令牌失效。jwt的内容可以公布，不是进行了加密，而是保证了唯一性，防止被篡改。（类似于身份证）。

3、生成令牌

先引入依赖：

生成的jwt内容为：

eyJhbGciOiJIUzI1NiJ9.eyJpZCI6MSwidXNlcm5hbWUiOiJsaXNpIiwiaWF0IjoxNzEwNTc2NjcwLCJleHAiOjE3MTA1ODAyNzB9.FQQTi586Wp_9S-tCjO1rmHhHqSuFWdkXF3KlLcotgFU

解析该jwt：

4、检验令牌

运行结果：

只要结果不为空就表明令牌是正确的。

四、JWT登陆功能&强制登陆功能

1、JWT实现登陆功能

后端处理：

前端请求+响应：

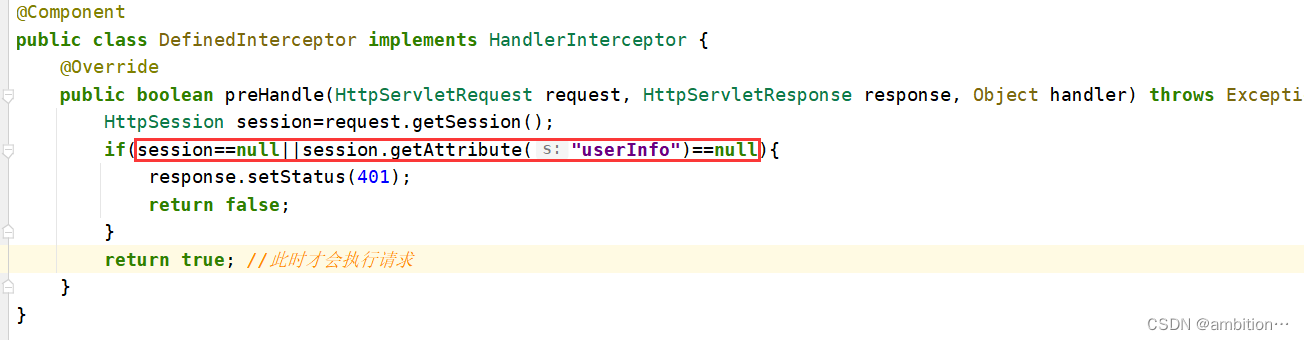
2、强制登陆功能

使用拦截器进行强制登陆，判断用户令牌是否正确。从本地存储中拿出令牌放在请求header中，根据拿到的内容判断是否能拿到负载内容。

由于每个页面都要进行强制登陆判断，所以将从本地存储中拿出令牌放在请求header中的操作统一放在common.js中，且要在发送请求前放在header中：

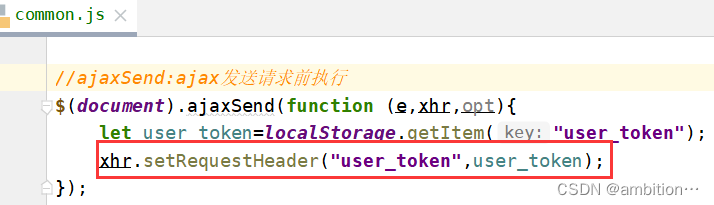
3、运行效果

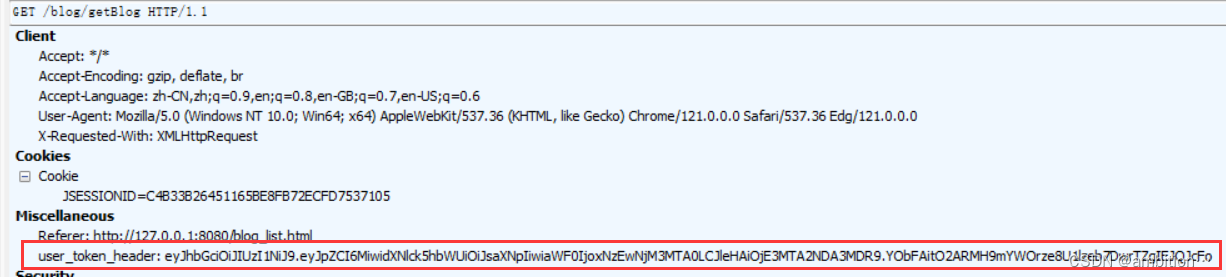
此时就能正确显示博客列表页了。

五、加密/加盐

对于数据库中的敏感信息：例如密码等，需要对其加密，不然黑客入侵后就会获取到用户的密码，造成一定的损失。

1、加密方式

（1）对称加密

对于明文的加密和密文的解密使用的是同一种密钥。常见算法有：AES,DES,3DES,RC4,RC5,RC6

（2）非对称加密

明文的加密采用公钥，密文的解密采用私钥。公钥可以公开，私钥不可以公开。常见算法有：RSA,DSA,ECDSA,ECC；

（3）摘要加密

将任意长度的明文转为固定长度的数据，不可逆，无法解密。对于相同的明文，进行摘要加密后结果相同。常见算法有：MD5,SHA1,SHA2,CRC。

2、基于MD5的加密

（1）MD5弊端

博客系统采用MD5加密方式，将密码转换为固定长度的数据。但只使用MD5存在弊端：

①虽然MD5不可逆，但对于密码较短的，可以借助工具进行解密；

②密码一样的用户，MD5转换后是一样的，一旦一个用户暴露，其他也会暴露。

（2）加盐

可以对于密码加上固定长度的随机值(盐值)，明文+盐值---->进行MD5加密。

还需考虑一个问题：在进行验证时，我们如何拿到盐？？？

可以将盐值插入在MD5加密后的数据里，验证时分离出加密结果和盐值即可。

为了简单：我们就直接将盐值拼接在加密结果后面了。

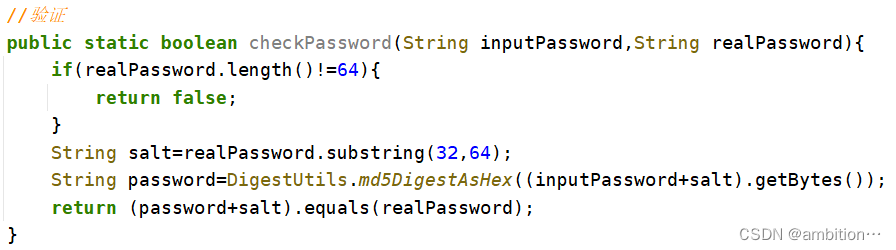
（3）生成加密密码

将数据库修改为：

进行登陆验证：

六、博客系统部分代码

1、登陆功能

（1）客户端请求+响应

（2）服务器响应

2、展示博客列表功能

（1）客户端请求+响应

（2）服务器响应

3、展示博客详情功能

（1）客户端请求+响应

（2）服务器响应

4、更新博客功能

（1）客户端请求+响应

（2）服务器响应

5、删除博客功能

（1）客户端请求+响应

（2）服务器响应

6、发布博客功能

（1）客户端请求+响应

（2）服务器响应

7、退出博客登陆

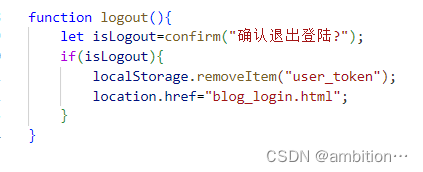
8、强制登陆功能

若需要全部源码，可以进入：葛雅宁 (ge-yaning) - Gitee.com

点击java学习下的基于spring下的博客管理系统：