LeetCode 53. 最大子数组和
LeetCode 56. 合并区间
LeetCode 189. 轮转数组
LeetCode 238. 除自身以外数组的乘积
LeetCode 41. 缺失的第一个正数

普通数组

最大子数组和

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组是数组中的一个连续部分。

class Solution {
    public int maxSubArray(int[] nums) {
        int[] dp = new int[nums.length];
        dp[0] = nums[0];

        int result = dp[0];
        for (int i = 1; i < nums.length; i++) {
            dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
            result = Math.max(result, dp[i]);
        }
        return result;
    }
}

合并区间

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

• 按照左端点升序排序
• 然后逻辑判断
• 将第一个区间加入List
• 后续空间，如果左端点大于数组中最后一个区间的右端点，则直接加入
• 反之，把List中最后一个区间的右端点改成最大值

class Solution {
    public int[][] merge(int[][] intervals) {
        if (intervals.length == 0) return new int[0][2];

        Arrays.sort(intervals, new Comparator<int[]> () {
            public int compare(int[] interval1, int[] interval2) {
                return interval1[0] - interval2[0];
            }
        });

        List<int[]> result = new ArrayList<int[]>();
        for (int i = 0; i < intervals.length; i++) {
            if (result.size() == 0 || result.get(result.size() - 1)[1] < intervals[i][0]) {
                result.add(new int[]{intervals[i][0], intervals[i][1]});
            } else {
                result.get(result.size() - 1)[1] = Math.max(result.get(result.size() - 1)[1], intervals[i][1]);
            }
        }
        return result.toArray(new int[result.size()][2]);
    }
}

轮转数组

给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

class Solution {
    public void rotate(int[] nums, int k) {
        int n = nums.length;
        int[] newArr = new int[n];

        for (int i = 0; i < n; i++) {
            newArr[(i + k) % n] = nums[i];
        }
        
        System.arraycopy(newArr, 0, nums, 0, n);
    }
}

• 多次翻转，空间复杂度为 $O(1)$

class Solution {
    public void rotate(int[] nums, int k) {
        reverse(nums, 0, nums.length - 1);
        reverse(nums, 0, k % nums.length - 1);
        reverse(nums, k % nums.length, nums.length - 1);
    }

    private void reverse(int[] array, int start, int end) {
        for (int i = start, j = end; i < j; i++, j--) {
            int temp = array[i];
            array[i] = array[j];
            array[j] = temp;
        }
    }
}

除自身以外数组的乘积

给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。

题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。

请 不要使用除法，且在 O(n) 时间复杂度内完成此题。

你可以在 O(1) 的额外空间复杂度内完成这个题目吗？

• 化成左右乘积的形式

class Solution {
    public int[] productExceptSelf(int[] nums) {
        // answer[i] = 左边的乘积×右边的乘积
        // 双指针

        int[] ans = new int[nums.length];
        Arrays.fill(ans, 1);
        int before = 1;
        int after = 1;
        for (int i = 0 , j = nums.length - 1; i < nums.length; i++, j--) {
            ans[i] *= before;
            ans[j] *= after;
            before *= nums[i];
            after *= nums[j];
        }
        return ans;
    }
}

缺失的第一个正数

给你一个未排序的整数数组 nums ，请你找出其中没有出现的最小的正整数。

请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案.

输入：nums = [1,2,0]
输出：3
解释：范围 [1,2] 中的数字都在数组中。

• 如果没有时空复杂度要求：

  • 把数放到哈希表中，从1 开始枚举正整数，判断是否在哈希表中
  • 可以从1 开始枚举正整数，遍历数组，判断是否在数组中

• 第一种做法的时间复杂度为 $O(N)$，空间复杂度为$O(N)$

• 第二种做法的时间复杂度为 $O(N^2)$，空间复杂度为$O(1)$

• 「真正」满足时间复杂度为 $O(N)$，空间复杂度为 $O(1)$ 的算法是不存在的。

• 但可以修改题目给的数组

• 一个长度为$N$ 的数组，其中没有出现的最小正整数只能在 $[1,N+1]$ 中

• 如果 $[1,N]$ 都出现了，那么答案是 $N+1$

• 否则答案是 $[1,N]$ 中没有出现的最小正整数。

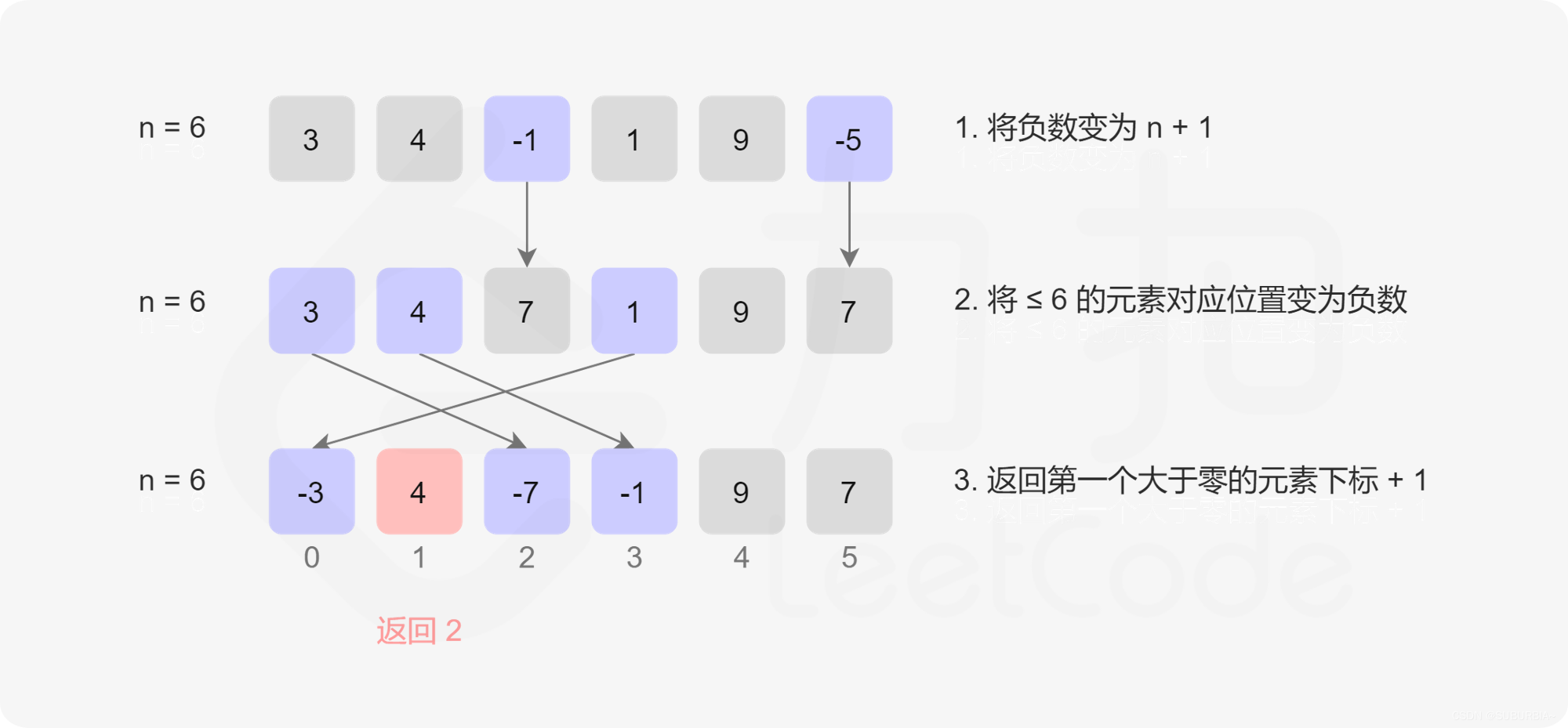
class Solution {
    public int firstMissingPositive(int[] nums) {
        // 负数变成 nums.length
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] <= 0) nums[i] = nums.length + 1;
        }

        // < nums.length 的变成负数，打上标记
        for (int i = 0; i < nums.length; i++) {
            if (Math.abs(nums[i]) <= nums.length) {
                nums[Math.abs(nums[i]) - 1] = -Math.abs(nums[Math.abs(nums[i]) - 1]);
            }
        }

        for (int i = 0; i < nums.length; i++) {
            if (nums[i] > 0) return i + 1;
        }
        return nums.length + 1;
    }
}

class Solution {
    public int firstMissingPositive(int[] nums) {
        int n = nums.length;
        for (int i = 0 ; i < n; i++) {
            while (nums[i] > 0 && nums[i] <= n && nums[nums[i] - 1] != nums[i]) {
                int temp = nums[nums[i] - 1];
                nums[nums[i] - 1] = nums[i];
                nums[i] = temp;
            }
        }

        for (int i = 0; i < n; i++){
            if (nums[i] != i + 1){
                return i + 1;
            }
        }

        return n + 1;
    }
}