Offer必备算法16_字符串_四道力扣题详解（由易到难）

news2024/12/28 4:45:04

①力扣14. 最长公共前缀

解析代码1（两两比较）

解析代码2（统一比较）

②力扣5. 最长回文子串

解析代码（中心拓展）

③力扣67. 二进制求和

解析代码

④力扣43. 字符串相乘

解析代码（无进位相乘）

本篇完。

①力扣14. 最长公共前缀

14. 最长公共前缀

难度简单

编写一个函数来查找字符串数组中的最长公共前缀。

如果不存在公共前缀，返回空字符串 ""。

示例 1：

输入：strs = ["flower","flow","flight"]
输出："fl"

示例 2：

输入：strs = ["dog","racecar","car"]
输出：""
解释：输入不存在公共前缀。

提示：

1 <= strs.length <= 200
0 <= strs[i].length <= 200
strs[i] 仅由小写英文字母组成

class Solution {
public:
    string longestCommonPrefix(vector<string>& strs) {

    }
};

解析代码1（两两比较）

解法1（两两比较）：可以先找出前两个的最长公共前缀，然后拿这个最长公共前缀依次与后面的字符串比较，这样就可以找出所有字符串的最长公共前缀。

class Solution {
public:
    string longestCommonPrefix(vector<string>& strs) {
        string ret = strs[0];
        for(int i = 1; i < strs.size(); ++i)
        {
            ret = TowlongestCommonPrefix(ret, strs[i]);
        }
        return ret;
    }

    string TowlongestCommonPrefix(string& str1, string& str2)
    {
        if(str1.size() > str2.size())
            swap(str1, str2);

        for(int i = 0; i < str1.size(); ++i)
        {
            if(str1[i] == str2[i])
                continue;
            else
                return str1.substr(0, i);
        }
        return str1;
    }
};

解析代码2（统一比较）

解法2（统一比较）：题目要求多个字符串的公共前缀，我们可以逐位比较这些字符串，哪一位出现了不同，就在哪一位截止。

class Solution {
public:
    string longestCommonPrefix(vector<string>& strs) {
        string ret = "";
        sort(strs.begin(), strs.end());
        for(int i = 0; i < strs[0].size(); ++i) // 遍历最小的字符串
        {
            int j = 1; // 第二行开始依次和第一行比较
            while(j < strs.size() && strs[0][i] == strs[j][i])
            {   // 注意j不要越界
                ++j;
            }
            if(j == strs.size())
            {
                ret += strs[0][i];
            }
            else
            {
                break;
            }
        }
        return ret;
    }
};

②力扣5. 最长回文子串

5. 最长回文子串

难度中等

给你一个字符串 s，找到 s 中最长的回文子串。

如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。

示例 1：

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

示例 2：

输入：s = "cbbd"
输出："bb"

提示：

1 <= s.length <= 1000
s 仅由数字和英文字母组成

class Solution {
public:
    string longestPalindrome(string s) {

    }
};

解析代码（中心拓展）

暴力解法是O（N^3），对于一个子串而言，如果它是回文串，并且长度大于 2，那么将它首尾的两个字母去除之后，它仍然是个回文串。如此这样去除，一直除到长度小于等于 2 时呢？长度为 1 的，自身与自身就构成回文，而长度为 2 的，就要判断这两个字符是否相等了。

从这个性质可以反推出来，从回文串的中心开始，往左读和往右读也是一样的。那么，是否可以枚举回文串的中心呢？从中心向两边扩展，如果两边的字母相同，就可以继续扩展，如果不同，就停止扩展。这样只需要一层 for 循环，就可以完成之前两层 for 循环的工作量。

class Solution {
public:
    string longestPalindrome(string s) {
        int n = s.size(), begin = 0, maxlen = 0;
        for(int i = 0; i < n; ++i)
        {
            int left = i, right = i, cnt = 0; // 奇数长度拓展
            while(left >= 0 && right < n && s[left] == s[right])
            {
                --left;
                ++right;
                cnt = right - left - 1;
            }
            if(cnt > maxlen)
            {
                begin = left + 1;
                maxlen = cnt;
            }

            left = i, right = i + 1, cnt = 0; // 偶数长度拓展
            while(left >= 0 && right < n && s[left] == s[right])
            {
                --left;
                ++right;
                cnt = right - left - 1;
            }
            if(cnt > maxlen)
            {
                begin = left + 1;
                maxlen = cnt;
            }
        }
        return s.substr(begin, maxlen);
    }
};

③力扣67. 二进制求和

67. 二进制求和

难度简单

给你两个二进制字符串 a 和 b ，以二进制字符串的形式返回它们的和。

示例 1：

输入:a = "11", b = "1"
输出："100"

示例 2：

输入：a = "1010", b = "1011"
输出："10101"

提示：

1 <= a.length, b.length <= 10^4
a 和 b 仅由字符 '0' 或 '1' 组成
字符串如果不是 "0" ，就不含前导零

class Solution {
public:
    string addBinary(string a, string b) {

    }
};

解析代码

思路是模拟十进制中列竖式计算两个数之和的过程。但是这是二进制求和，不是逢十进一，而是逢二进一。

class Solution {
public:
    string addBinary(string a, string b) {
        if(a.size() > b.size())
            swap(a, b); // 让b是长的

        string ret = "" ;
        int val = 0, carry = 0;
        for(int i = b.size()-1, j = a.size()-1; i >= 0 ; --i)
        {
            if(j >= 0)
                val = (a[j--] - '0') + (b[i] - '0') + carry;
            else
                val = (b[i] - '0') + carry;
            carry = val / 2;
            ret += ((val % 2) + '0');
        }
        if(carry)
            ret += (carry + '0');
        reverse(ret.begin(), ret.end());
        return ret;
    }
};

④力扣43. 字符串相乘

43. 字符串相乘

难度中等

给定两个以字符串形式表示的非负整数 num1 和 num2，返回 num1 和 num2 的乘积，它们的乘积也表示为字符串形式。

注意：不能使用任何内置的 BigInteger 库或直接将输入转换为整数。

示例 1:

输入: num1 = "2", num2 = "3"
输出: "6"

示例 2:

输入: num1 = "123", num2 = "456"
输出: "56088"

提示：

1 <= num1.length, num2.length <= 200
num1 和 num2 只能由数字组成。
num1 和 num2 都不包含任何前导零，除了数字0本身。

class Solution {
public:
    string multiply(string num1, string num2) {

    }
};

解析代码（无进位相乘）

解法1是模拟小学的列竖式运算，直接进位相加，这样要处理后面的0，很麻烦

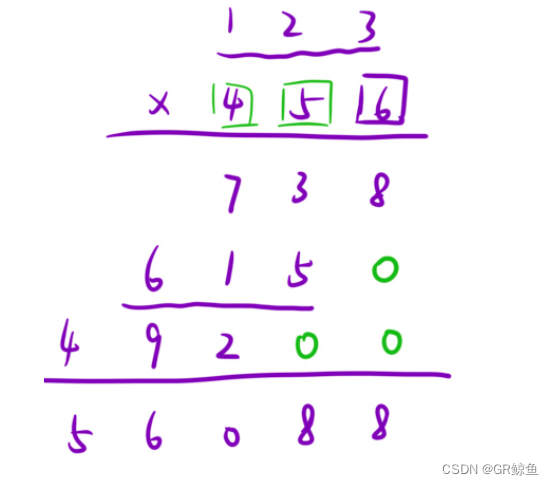
这里看一种优化过的无进位相乘的解法：是在计算两数相乘的时候，先不考虑进位，等到所有结果计算完毕之后，再去考虑进位。如下图：

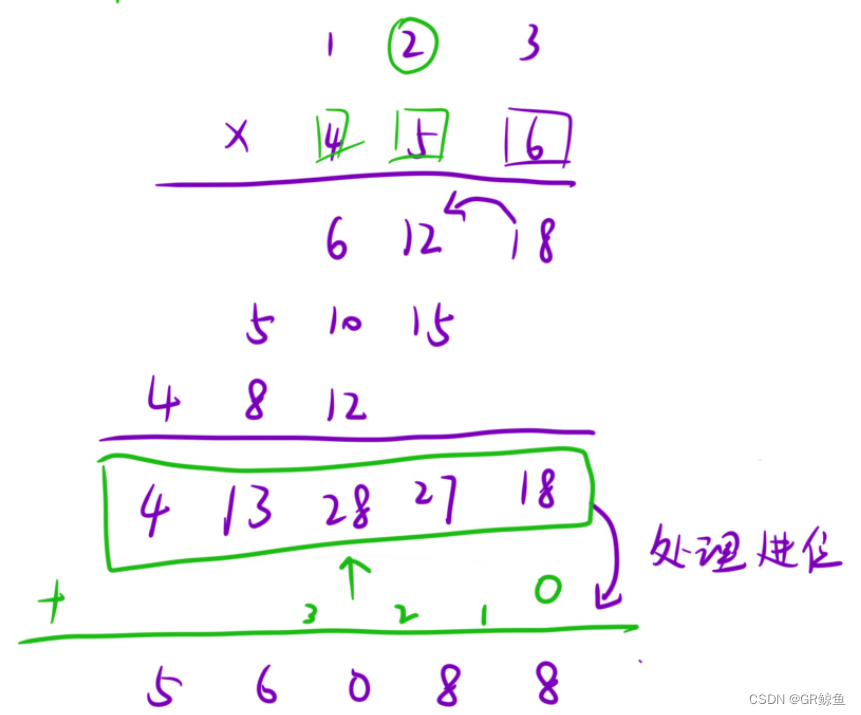
可以自己模拟没优化的解法，官方题解有答案，这里模拟无进位相乘的解法：

class Solution {
public:
    string multiply(string num1, string num2) {
        int n1 = num1.size(), n2 = num2.size();
        vector<int> tmp(n1 + n2 - 1);
        reverse(num1.begin(), num1.end());
        reverse(num2.begin(), num2.end());

        for(int i = 0; i < n1; ++i)
        {
            for(int j = 0; j < n2; ++j)
            {
                tmp[i+j] += (num1[i] - '0') * (num2[j] - '0');
            }
        }
        string ret = "";
        int carry = 0;
        for(auto& e : tmp)
        {
            cout << e << " ";
            ret += ((e + carry) % 10 + '0');
            carry = (e + carry) / 10; 
        }
        if(carry)
            ret += (carry + '0');

        while(ret.size() > 1 && ret.back() == '0') 
            ret.pop_back(); // 处理前导0

        reverse(ret.begin(), ret.end());
        return ret;
    }
};