目录
一. PriorityQueue的特性
二. PriorityQueue常用接口介绍
1. 优先级队列的构造
2. 转成大根堆存储方法:
3. 插入/删除/获取优先级最高的元素
三. Top-k问题
一. PriorityQueue的特性

import java . util . PriorityQueue ;
二. PriorityQueue常用接口介绍
1. 优先级队列的构造

// 创建一个空的优先级队列,底层默认容量是 11PriorityQueue < Integer > q1 = new PriorityQueue <> ();// 创建一个空的优先级队列,底层的容量为 initialCapacityPriorityQueue < Integer > q2 = new PriorityQueue <> ( 100 );// 用 ArrayList 对象来构造一个优先级队列的对象ArrayList < Integer > list = new ArrayList <> ();list . add ( 4 );list . add ( 3 );list . add ( 2 );list . add ( 1 );PriorityQueue < Integer > q3 = new PriorityQueue <> ( list );
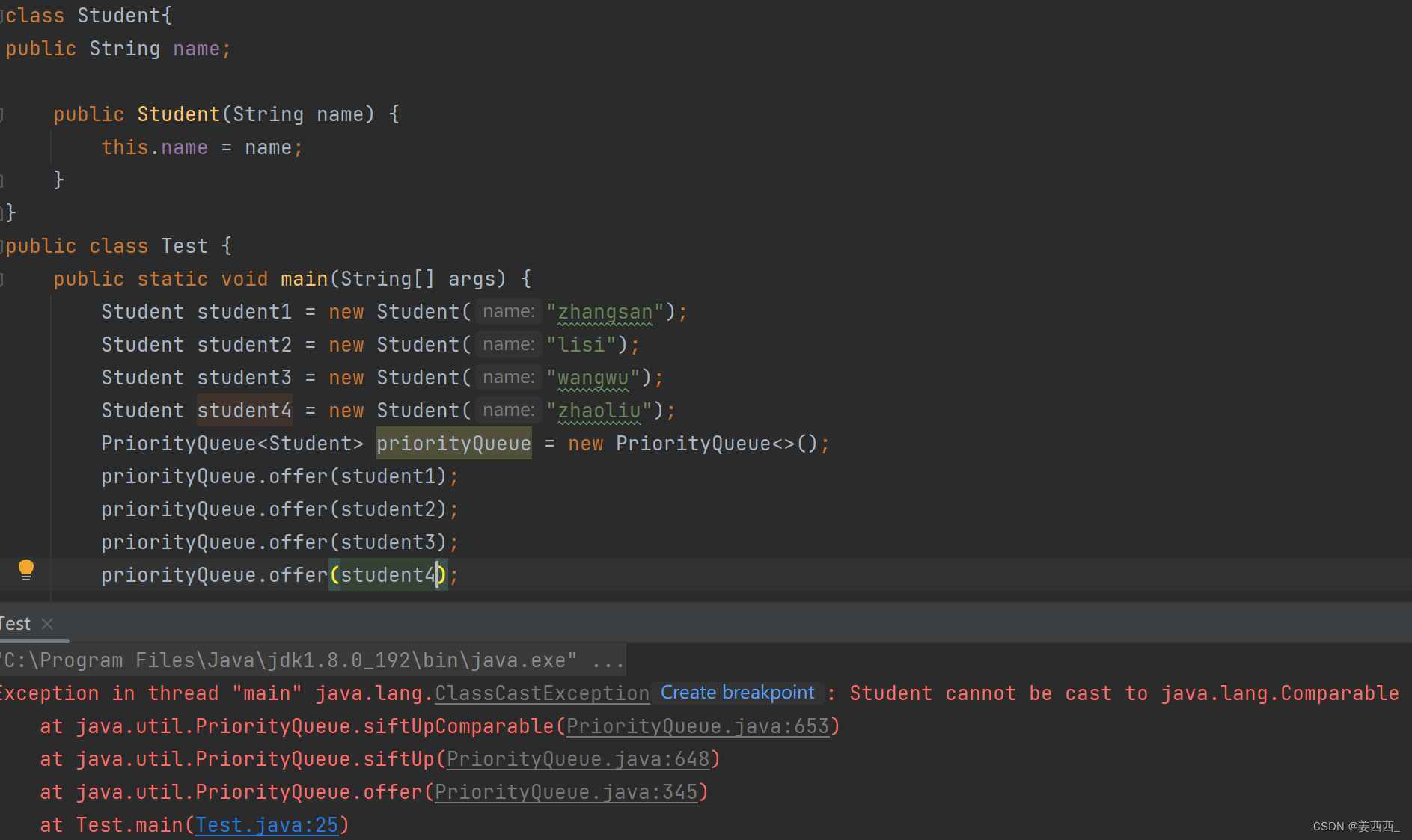
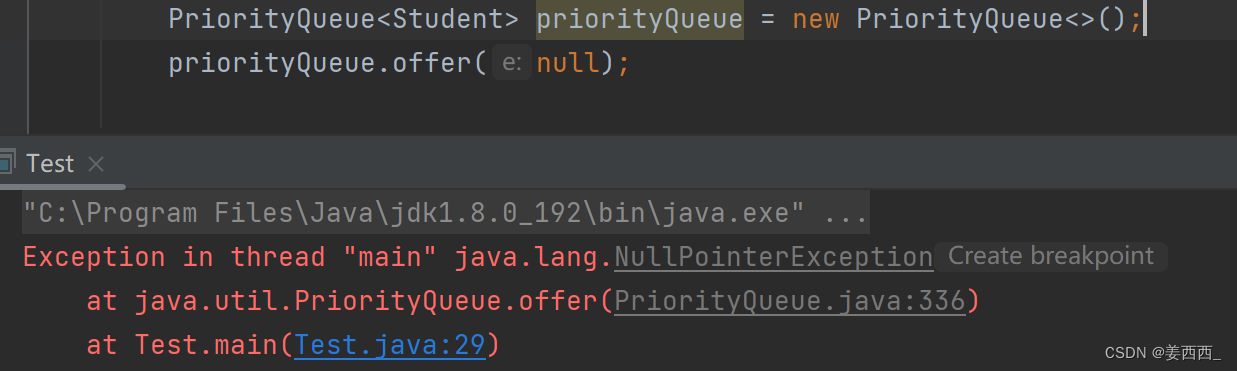
注意:默认情况下,PriorityQueue队列是小根堆,如果需要其他比较方法需要用户提供比较器
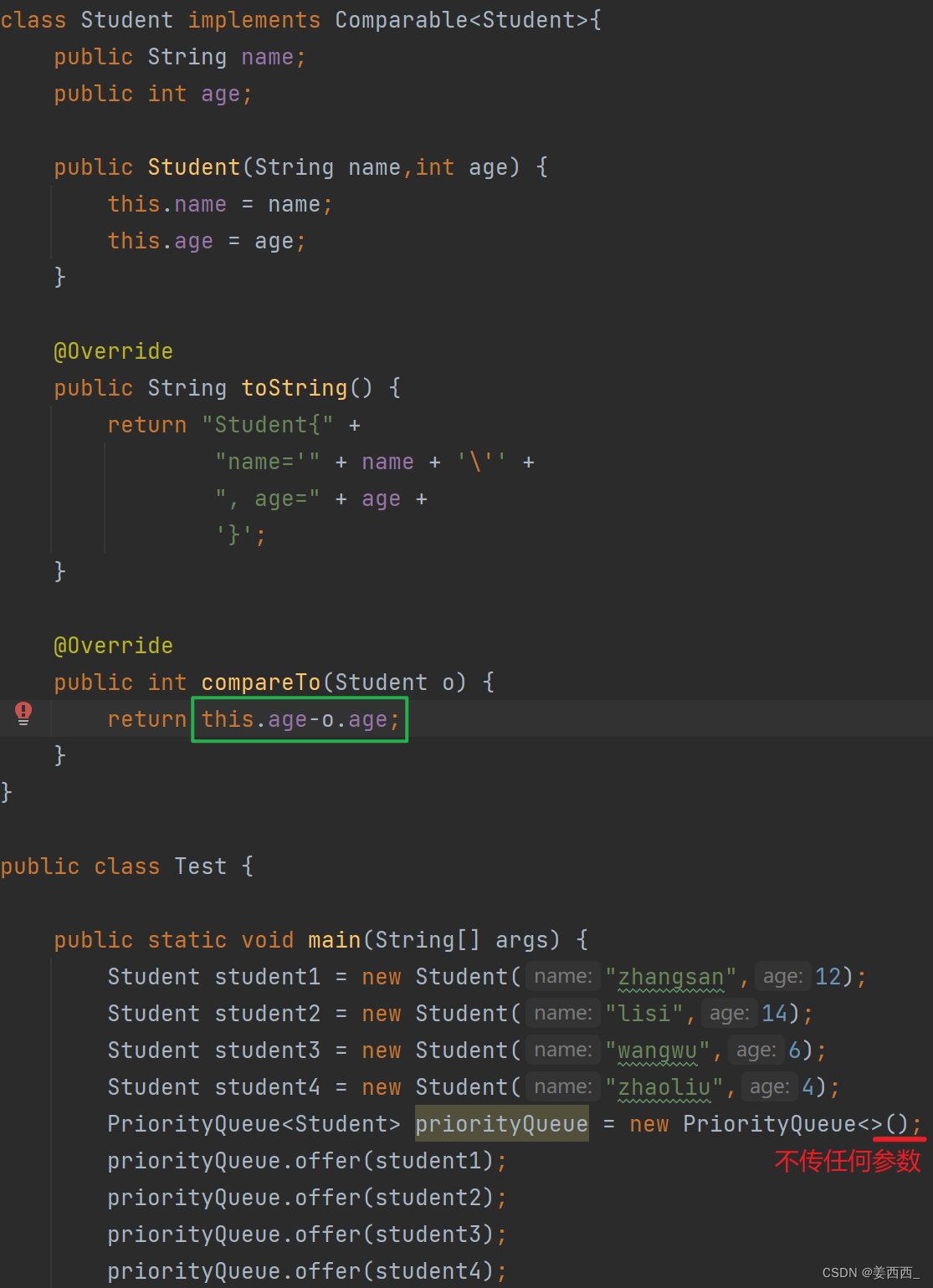
例如上面的学生类, 如果想要插入优先级对列, 必须继承Comparator接口, 并重写CompareTo方法, 提供比较方法, 就可以传入优先级队列
class Student implements Comparable<Student>{
public String name;
public int age;
public Student(String name,int age) {
this.name = name;
this.age = age;
}
@Override
public int compareTo(Student o) {
return this.age-o.age;
}
}
public class Test {
public static void main(String[] args) {
Student student1 = new Student("zhangsan",12);
Student student2 = new Student("lisi",14);
Student student3 = new Student("wangwu",6);
Student student4 = new Student("zhaoliu",4);
PriorityQueue<Student> priorityQueue = new PriorityQueue<>();
priorityQueue.offer(student1);
priorityQueue.offer(student2);
priorityQueue.offer(student3);
priorityQueue.offer(student4);
System.out.println(student1.compareTo(student2));
}
}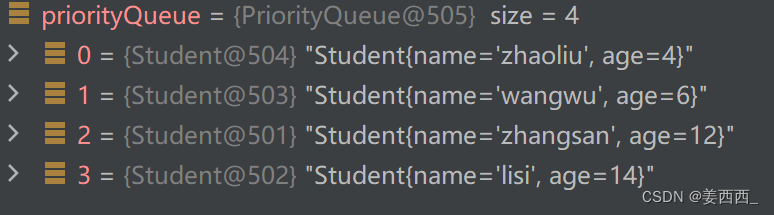
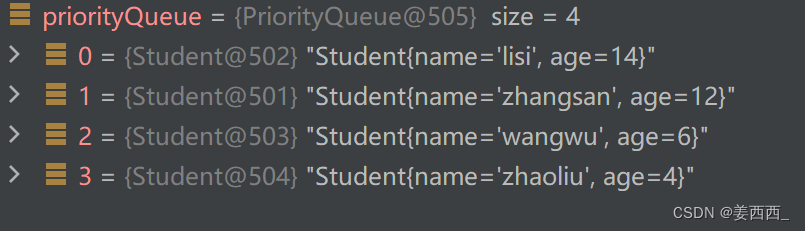
可以看到是小根堆存储的
第四种构造方法:
我们点进去PriorityQueue的源码就会发现, 构造方法还可以传比较器

我们可以写一个比较器, 类可以不用继承Comparator接口了, 接着通过传比较器就可以进行比较了, 就可以插入优先级队列
class Student {
public String name;
public int age;
public Student(String name,int age) {
this.name = name;
this.age = age;
}
@Override
public String toString() {
return "Student{" +
"name='" + name + '\'' +
", age=" + age +
'}';
}
}
class NameComparator implements Comparator<Student> {
@Override
public int compare(Student o1,Student o2) {
return o1.name.compareTo(o2.name);
}
}
public class Test {
public static void main(String[] args) {
Student student1 = new Student("zhangsan",12);
Student student2 = new Student("lisi",14);
Student student3 = new Student("wangwu",6);
Student student4 = new Student("zhaoliu",4);
NameComparator nameComparator = new NameComparator();
PriorityQueue<Student> priorityQueue = new PriorityQueue<>(nameComparator);
priorityQueue.offer(student1);
priorityQueue.offer(student2);
priorityQueue.offer(student3);
priorityQueue.offer(student4);
System.out.println(priorityQueue.peek());//验证:如果是通过name进行排序, 那么堆顶元素应该是lisi
System.out.println(nameComparator.compare(student1,student2));
}那么, 如果我们想要大根堆该怎么实现呢?
2. 转成大根堆存储方法:
转成大根堆的第一种方式:重写comepareTo接口
先来看一下源码中小根堆是怎么实现的:
还是学生的类举例:
此时是小根堆存储
offer():
siftUp():
因为我们没有传入比较器, 那么就进入else中, 进入siftUpComrarable()中
siftUpComrarable():
我们可以看到, 使用的是compareTo方法, key表示新传入数字的值, e表示此节点的父亲节点的值, key.compareTo(e), compareTo是通过key - e来计算的, 如果key.compareTo(e) >= 0 , 说明key>e, 就会break, 不交换两个数, 此时的存储顺序是e -> key, 那么存储的方式就是小根堆
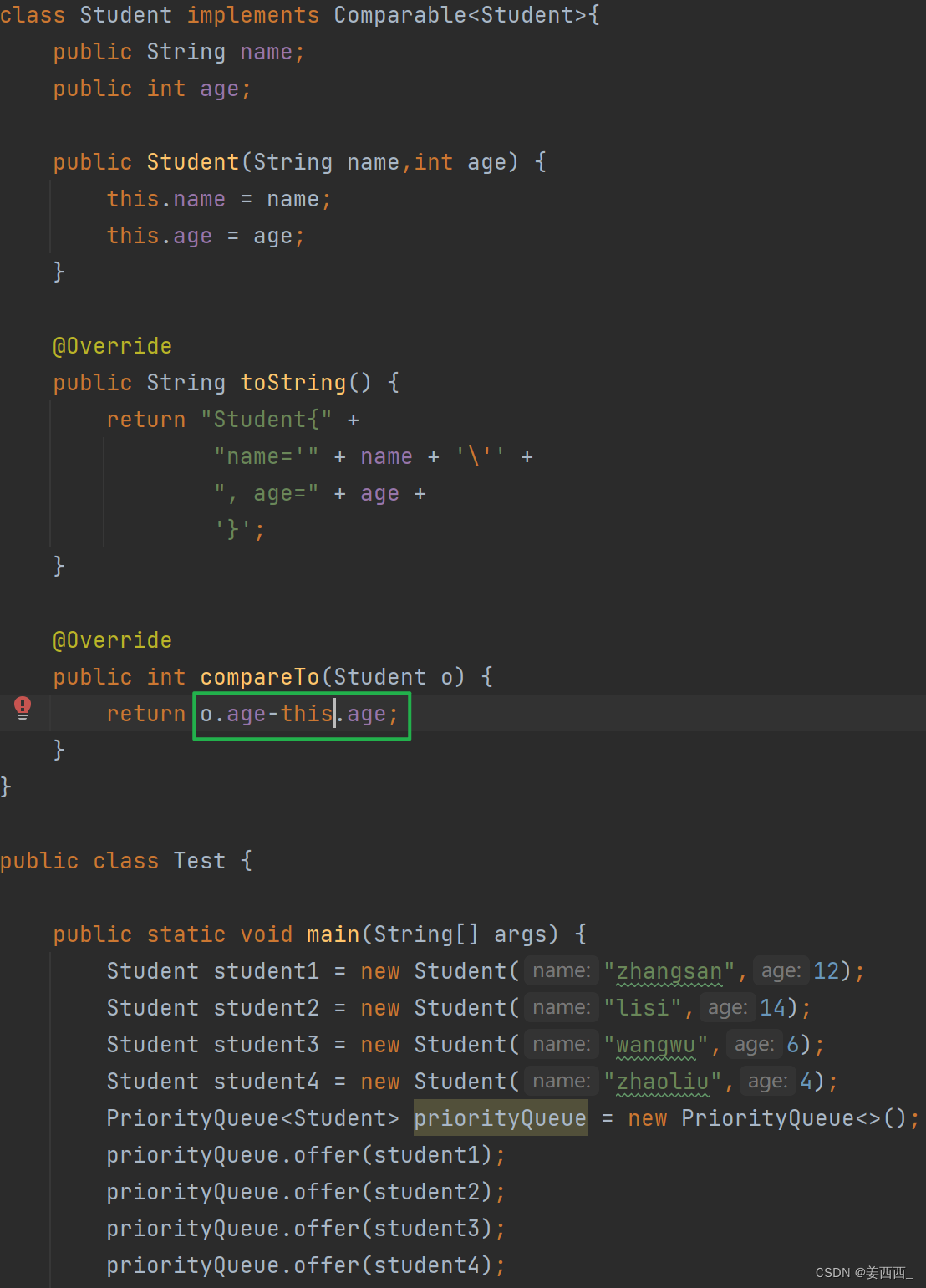
如果我们重写compareTo方法, 通过e - key进行计算, 那么如果key.compareTo(e) >= 0 , 说明key<e, 就会break, 不交换两个数, 此时的存储顺序还是e -> key, 那么存储的方式就是大根堆
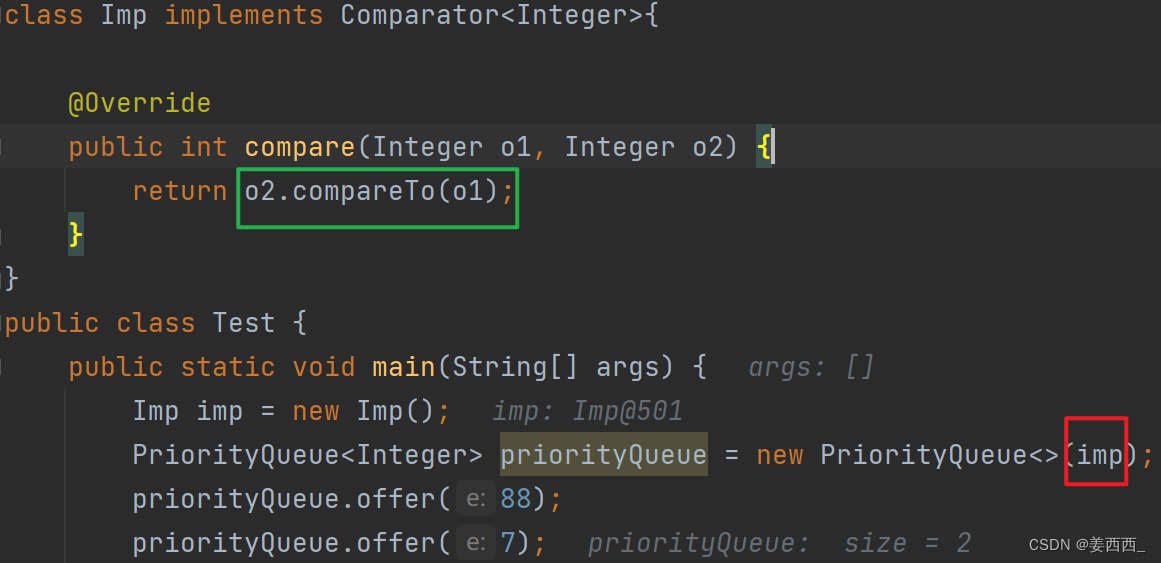
那么, 我们将上面绿的框的代码进行更改
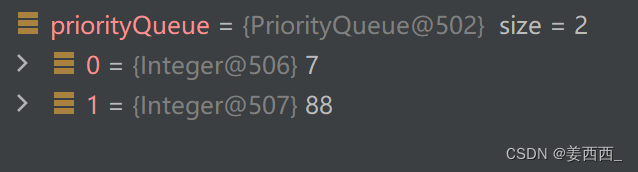
变成大根堆存储了!
转成大根堆的第二种方式:传入比较器
先写一个简单的代码:
offer():
siftUp():
假设我们传入了比较器, 就会进入siftUsingComparator方法中
siftUsingComparator():
可以看到调用的是比较器中的compare方法, 所以我们可以在比较器中更改比较的方法, 来实现大根堆还是小根堆存储
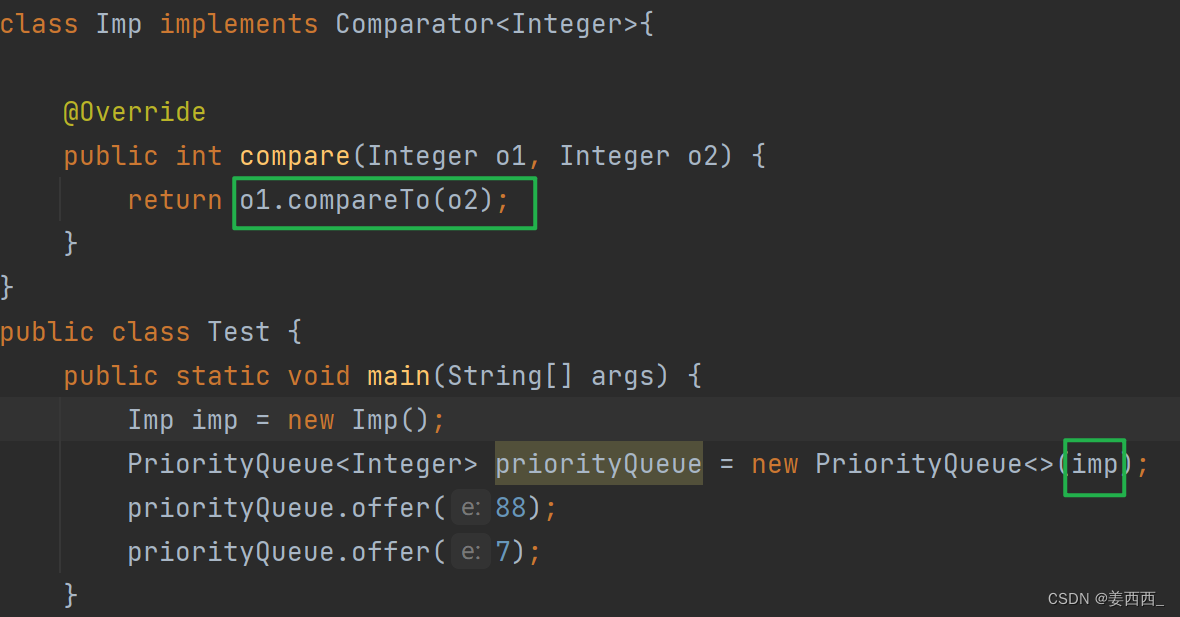
我们可以写一个比较器:
此时是小根堆存储
此时是大根堆存储
3. 插入/删除/获取优先级最高的元素

三. Top-k问题
思路:
找最大最小的问题, 我们首先想到使用堆, 因为如果是大根堆, 那么堆顶元素就是最大值, 如果是小根堆, 那么堆顶元素就是小根堆
思路1:我们可以将所有的数据放入堆中, 想到得到前k小的数据, 就循环弹出k个元素即可, 但上述思路的时间复杂度很高
思路2:为了尽可能减小时间复杂度, 我们可以建立只有k个结点的堆,可以取数组的前k个数, 但是找前k小的元素, 就要建立大根堆, 这样堆顶元素就是k个元素中最大的, 我们从数组下标为k的位置开始遍历, 用数组后面的数据和堆顶元素进行比较, 如果有比堆顶元素小的元素, 那么就删除堆顶元素, 将这个数放进来, 此时堆顶元素就是此时堆中最大的元素, 循环比较下去, 直到遍历完成数组, 此时数组中存放的就是最小的k个数, 存放在返回数组中即可
class Imp implements Comparator<Integer>{
public int compare(Integer o1,Integer o2){
return o2 - o1;
}
}
class Solution {
public static int[] smallestK(int[] arr, int k) {
Imp imp = new Imp();
int[] tmp = new int[k];
if(k == 0){
return tmp;
}
PriorityQueue<Integer> maxHeap = new PriorityQueue<>(imp);
for (int i = 0; i < k; i++) {
maxHeap.offer(arr[i]);
}
int i = k;
while(i < arr.length){
if(maxHeap.peek() > arr[i]){
maxHeap.poll();
maxHeap.offer(arr[i]);
}
i++;
}
for (int j = 0; j < k; j++) {
tmp[j] = maxHeap.poll();
}
return tmp;
}
}