【Super数据结构】先进先出/后进先出，队列和栈代码实现+应用场景

news2024/11/23 3:28:02

在这里插入图片描述

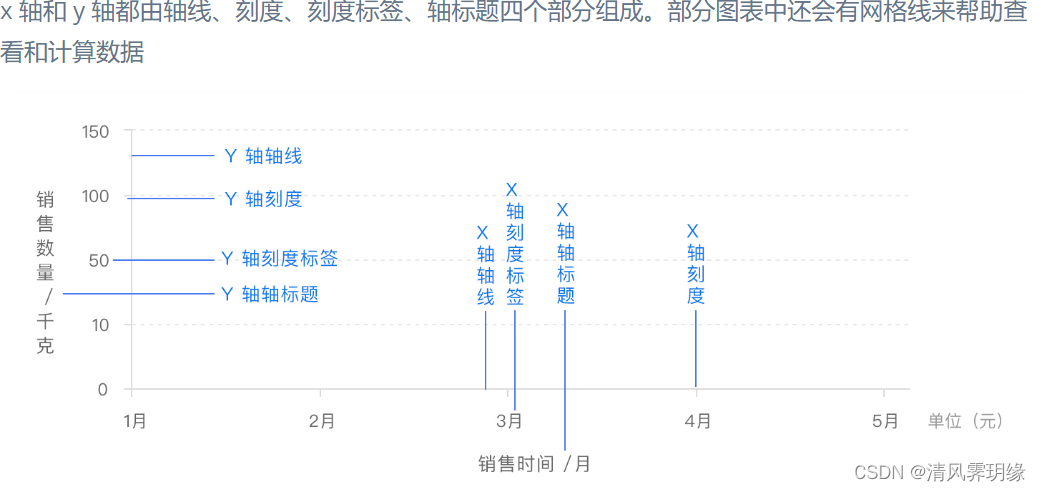
🏠关于此专栏：Super数据结构专栏将使用C/C++语言介绍顺序表、链表、栈、队列等数据结构，每篇博文会使用尽可能多的代码片段+图片的方式。
🚪归属专栏：Super数据结构
🎯每日努力一点点，技术累计看得见

文章目录

  • 栈
    • 栈的概念和结构
    • 栈的实现
  • 队列
    • 队列的概念及结构
    • 队列的实现
    • 环形队列
  • 综合巩固

栈

老式的手电筒是装电池的，如下图所示。1号电池装入后，再装第2号电池。如果想从中取出电池，只有先取出第2号电池，才能取第1号电池。像这种后进入先出来的结构，在数据结构中被称为栈。
在这里插入图片描述

栈的概念和结构

栈是一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。

栈有两种常用的操作，从栈顶取数据以及将输入放入栈中。对于这两种操作，我们经常将它们称为出栈和压栈。

压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。
出栈：栈的删除操作叫做出栈。出数据也在栈顶。
在这里插入图片描述

栈的实现

栈的实现一般可以使用数组或者链表实现，相对而言数组的结构实现更优一些。因为数组在尾上插入、删除数据的代价比较小。下面使用数组实现栈结构。

在开始实现栈结构之前，我们要先定义一个栈结构。我们需要一个动态开辟的数组，用它存储栈内元素，一个变量记录当前栈顶的位置，还需要一个变量记录栈当前的容量。（这里的栈顶指针top指向栈顶元素的下一位置）

typedef int STDataType;

typedef struct Stack
{
	STDataType* a;
	int top;
	int capacity;
}Stack;

下面给出栈的各个接口↓↓↓

//初始化
void StackInit(Stack* s, int n);
//销毁
void StackDestory(Stack* s);
//入栈
void StackPush(Stack* s, STDataType x);
//出栈
void StackPop(Stack* s);
//获取栈顶元素
STDataType StackTop(Stack* s);
//判断栈是否为空
bool IsEmpty(Stack* s);
//获取栈已保存元素个数
int StackSize(Stack* s);

栈的初始化
首先给出栈的初始化操作，根据用户给出的初始容量n，为动态数组a开辟n个空间，并将capacity改为n。由于初始时没有保存任何元素，故将栈顶指针top指向0。

void StackInit(Stack* s, int n)
{
	assert(s);
	s->a = (STDataType*)malloc(sizeof(STDataType) * n);
	s->top = 0;
	s->capacity = n;
}

栈的销毁
栈在堆区开辟空间，栈不再使用时，需要将开辟的空间释放掉。再将top指针和容量置为0。

void StackDestory(Stack* s)
{
	assert(s);
	free(s->a);
	s->capacity = s->top = 0;
}

入栈操作
在入栈前，需要检查容量是否足够，如果容量不足，则扩容2倍空间。由于栈顶指针top指向的是栈顶元素的下一个位置，所以我们要先在top下标位置保存入栈元素，再将top指针加1。

在这里插入图片描述

void StackPush(Stack* s, STDataType x)
{
	assert(s);
	if (s->top == s->capacity)
	{
		s->a = (STDataType*)realloc(s->a, sizeof(STDataType) * s->capacity * 2);
		if (s->a == NULL)
		{
			perror("malloc error!\n");
			return 0;
		}
		s->capacity *= 2;
	}
	s->a[s->top++] = x;
}

出栈操作
如果栈中已经没有元素，此时应该禁止用户出栈。如果当前栈中有一个以上元素，我们只需要将栈顶指针top减一，即可完成出栈操作。

例如：有一个保存了4个元素的栈，初始时top指向栈顶元素的下一位置，如下图绿色箭头所示。当执行出栈操作后，top减1，top直向出栈前的栈顶元素。由于栈顶有效元素位置位于top指针以下，故此时红色top指针指向的数字4不是有效元素。
在这里插入图片描述

void StackPop(Stack* s)
{
	assert(s);
	assert(!IsEmpty(s));
	--s->top;
}

获取栈顶元素
由于栈顶指针top指向栈顶元素的下一个位置，我们在返回栈顶元素时，需要返回下标为top-1的元素。注意：在栈为空时，不允许用户获取栈顶元素。

STDataType StackTop(Stack* s)
{
	assert(s);
	assert(!IsEmpty(s));
	return s->a[s->top - 1];
}

判断栈是否为空 及 获取栈已存储元素数
由于栈顶指针top保存栈顶元素的下一个下标。因而，没有元素时它保存的值就是0，有元素时它就是栈中已存储的元素数。

bool IsEmpty(Stack* s)
{
	assert(s);
	return s->top == 0;
}

int StackSize(Stack* s)
{
	assert(s);
	return s->top;
}

队列

我们去奶茶店买奶茶时，需要按先来先点餐/取餐的方式。类似的场景包括医院叫号、银行叫号等等。生活中存在着大量的先到先服务的场景，我们将这种排队结构称之为队列。
在这里插入图片描述

队列的概念及结构

队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出FIFO(First In First Out) 。

入队列：进行插入操作的一端称为队尾
出队列：进行删除操作的一端称为队头
在这里插入图片描述

队列的实现

队列也可以数组和链表的结构实现，使用链表的结构实现更优一些，因为如果使用数组的结构，出队列在数组头上出数据，效率会比较低。

在开始实现之前，我们一样定义一个队列的存储结构。由于这里使用单链表结构实现队列，所以需要先创建链表结点结构QNode。队列需要保存头和尾，因而在Queue结构中需要存储头尾结点。

typedef int QDataType;

typedef struct QueueNode
{
	QDataType val;
	struct QueueNode* next;
}QNode;

typedef struct Queue
{
	QNode* head;
	QNode* tail;
}Queue;

接下来一起看看队列的各个接口↓↓↓

void QueueInit(Queue* q);

void QueueDestory(Queue* q);

void QueuePush(Queue* q, QDataType x);

void QueuePop(Queue* q);

QDataType QueueFront(Queue* q);

QDataType QueueBack(Queue* q);

int QueueSize(Queue* q);

bool IsEmpty(Queue* q);

队列初始化
队列初始时没有任何元素，我们应该让它的头尾指针均指向空。
在这里插入图片描述

void QueueInit(Queue* q)
{
	assert(q);
	q->head = q->tail = NULL;
}

队列的销毁
头结点指向第一个元素的结点，我通过用next指针保存头结点的下一个结点，释放完头指针指向的结点后，再让它等于next指针，next指针再指向头指针的下一个结点…（以此类推）。当头指针为空时，整个队列就销毁完成了。注意，尾指针还不是空，还需要将它置空。

void QueueDestory(Queue* q)
{
	assert(q);
	while (q->head != NULL)
	{
		QNode* next = q->head->next;
		free(q->head);
		q->head = next;
	}
	q->tail = NULL;
}

入队操作
在队列中新增元素，只能在队尾添加。当队列还没有任何元素时，我们需要创建一个结点保存新元素，并将头尾指针指向它；如果队列中已经有元素时，我们只需要将尾结点的next域改为新结点，并将尾指针指向新添加的结点即可。
在这里插入图片描述

void QueuePush(Queue* q, QDataType x)
{
	assert(q);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	newnode->val = x;
	newnode->next = NULL;
	if (q->head == NULL)
	{
		q->head = q->tail = newnode;
	}
	else
	{
		q->tail->next = newnode;
		q->tail = newnode;
	}
}

出队操作
如果队列中没有任何元素，则不允许用户出队。如果此时队列中仅有一个元素，则将它出队后，需要将头尾指针置空；如果队列中不止一个元素，则要先保存头指针的下一个结点，在将头结点删除后，将头指针改为新的头结点。
在这里插入图片描述

void QueuePop(Queue* q)
{
	assert(q);
	assert(!IsEmpty(q));
	if (q->head == q->tail)
	{
		free(q->head);
		q->head = q->tail = NULL;
	}
	else
	{
		QNode* newHead = q->head->next;
		free(q->head);
		q->head = newHead;
	}
}

获取头部元素
头指针指向的就是第一个结点的地址，只要返回它指向的结点的val域即可。

QDataType QueueFront(Queue* q)
{
	assert(q);
	assert(!IsEmpty(q));
	return q->head->val;
}

获取尾部元素
尾指针指向的就是最后一个结点的地址，只要返回它指向的结点的val域即可。

QDataType QueueBack(Queue* q)
{
	assert(q);
	assert(!IsEmpty(q));
	return q->tail->val;
}

获取队列元素数量
使用一个新指针保存头指针保存的结点地址。通过不断向后移动，每次移动就记录一次长度，当走到空时，就将整个队列走完了。此时返回记录的长度即可。

int QueueSize(Queue* q)
{
	assert(q);
	int size = 0;
	QNode* cur = q->head;
	while (cur)
	{
		size++;
		cur = cur->next;
	}
	return size;
}

判断队列是否为空
如果头结点指针指向空，就说明整个队列为空。

bool IsEmpty(Queue* q)
{
	assert(q);
	return q->head == NULL;
}

环形队列

上面实现的队列使用的是链表。假如我们使用的是数组存储队列那会是什么效果呢？

如果我们用一个长度为长度为8的数组存储队列元素。使用front存储队列开始的下标，rear指向队尾元素的下一个下标。如果元素入队列，则Queue[rear]=新元素，在++rear。如果元素出队列则让front++即可。
在这里插入图片描述
但如果不断入队不断出队，最终rear和front都会超出数组下标范围。此时我们通过在将rear++和front操作改为(rear+1)%len及(front+1)%len[其中len是数组长度]，就可以让rear或front回到数组最前面。这样就可实现数组空间重复利用。
在这里插入图片描述

但front==rear时我们已经定义为NULL，队列中没有元素。如果我们不断插入元素，则在插入8个元素后，rear和front重合，这时候就引出一个问题：rear==front到底是表示空，还是表示满呢？
在这里插入图片描述
为了解决这个问题，我们可以选择在front前面的一个元素不保存数据，使用(rear + 1) % len == front来作为队列已经满的依据，使用rear == front作为队列为空的依据。

这时计算队列的长度可以使用(rear - front + len) % len来计算。对于循环队列，这里只做介绍，不进行代码演示了。

综合巩固

学完上面的内容，下面我们来牛刀小试以下：

( ఠൠఠ )ﾉtest1：有效的括号

这里使用C语言时，需要将我们上述实现的栈结构全部包含进来。我了展示方便，这里给出的代码是C++语言。如果进入的是左括号，则直接保存到栈中；如果是右括号，则与栈中的括号匹配，不符合则返回false，如果匹配成功，则将栈顶弹出（因为这对括号已经能配对了）。直到s字符串走到结束时，这时候需要查看栈中是否还有括号，如果还有，说明这个字符串中的左括号多余右括号，故返回false；如果没有括号了，则说明所有括号都配对成功。

class Solution {
public:
    bool isValid(string s) {
        stack<char>stk;

        for(auto e : s)
        {
            if(!stk.empty() &&(
                (e == ')' && stk.top() == '(') ||
                (e == ']' && stk.top() == '[') ||
                (e == '}' && stk.top() == '{')
            ))
            {
                stk.pop();
            }
            else if(e == '(' || e == '[' || e == '{')
            {
                stk.push(e);
            }
            else
            {
                return false;
            }
        }

        return stk.empty();
    }
};

( ఠൠఠ )ﾉtest2：用队列实现栈

所有入栈的内容都保存在q1队列中，当需要获取栈顶元素时，则获取q1的队尾元素；当需要弹出栈顶元素，先将q1元素入到q2，直到只剩一个元素，这个元素用做返回，在返回前，将q2的内容再导会q1中。q2这里的作用仅仅是在q1需要做出栈时，作为q1队尾之前的各个元素保存的临时队列。

class MyStack {
public:
    MyStack() {

    }
    
    void push(int x) {
        q1.push(x);
    }
    
    int pop() {
        while(q1.size() > 1)
        {
            q2.push(q1.front());
            q1.pop();
        }
        int ret = q1.front();
        q1.pop();
        while(!q2.empty())
        {
            q1.push(q2.front());
            q2.pop();
        }
        return ret;
    }
    
    int top() {
        return q1.back();
    }
    
    bool empty() {
        return q1.empty();
    }
    queue<int>q1;//用于保存数据
    queue<int>q2;//用于临时交换
};

/**
 * Your MyStack object will be instantiated and called as such:
 * MyStack* obj = new MyStack();
 * obj->push(x);
 * int param_2 = obj->pop();
 * int param_3 = obj->top();
 * bool param_4 = obj->empty();
 */

( ఠൠఠ )ﾉtest3：用栈实现队列

使用一个输出栈和一个输入栈。当入队是元素均入到输入栈中；当输出栈为空时，将输入栈的元素全部入到输出栈，这样可以使得本来位于输入栈栈底的元素跑到输出栈的栈顶，这么操作就可以实现先进先出。

class MyQueue {
public:
    MyQueue() {

    }
    
    void push(int x) {
        pushstack.push(x);
    }
    
    int pop() {
        if(popstack.empty())
        {
            while(!pushstack.empty())
            {
                popstack.push(pushstack.top());
                pushstack.pop();
            }
        }
        int ret = popstack.top();
        popstack.pop();
        return ret;
    }
    
    int peek() {
        if(popstack.empty())
        {
            while(!pushstack.empty())
            {
                popstack.push(pushstack.top());
                pushstack.pop();
            }
        }
        return popstack.top();
    }
    
    bool empty() {
        return popstack.empty() && pushstack.empty();
    }
    stack<int>popstack;
    stack<int>pushstack;
};

/**
 * Your MyQueue object will be instantiated and called as such:
 * MyQueue* obj = new MyQueue();
 * obj->push(x);
 * int param_2 = obj->pop();
 * int param_3 = obj->peek();
 * bool param_4 = obj->empty();
 */

( ఠൠఠ )ﾉtest4：设计循环队列

这道题是对上面介绍的循环队列的实现。涉及下标的问题，多使用模运算符，实现下标从数组尾到头和头到尾的转换。

class MyCircularQueue {
public:
    MyCircularQueue(int k) {
        len = k + 1;
        a = (int*)malloc(sizeof(int) * len);
        front = rear = 0;
    }
    
    bool enQueue(int value) {
        if((rear + 1) % len == front) return false;
        a[rear] = value;
        rear = (rear + 1) % len;
        return true;
    }
    
    bool deQueue() {
        if(rear == front) return false;
        front = (front + 1) % len;
        return true;
    }
    
    int Front() {
        if(isEmpty()) return -1;
        return a[front];
    }
    
    int Rear() {
        if(isEmpty()) return -1;
        return a[(rear - 1 + len) % len];
    }
    
    bool isEmpty() {
        return front == rear;
    }
    
    bool isFull() {
        return (rear + 1) % len == front;
    }
    int* a;
    int front;
    int rear;
    int len;
};

/**
 * Your MyCircularQueue object will be instantiated and called as such:
 * MyCircularQueue* obj = new MyCircularQueue(k);
 * bool param_1 = obj->enQueue(value);
 * bool param_2 = obj->deQueue();
 * int param_3 = obj->Front();
 * int param_4 = obj->Rear();
 * bool param_5 = obj->isEmpty();
 * bool param_6 = obj->isFull();
 */

文章结语：这篇文章对时间复杂度、空间复杂度、数据结构与算法概念进行了简要的介绍。
🎈欢迎进入Super数据结构专栏，查看更多文章。
如果上述内容有任何问题，欢迎在下方留言区指正b(￣▽￣)d

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1532055.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

HarmonyOS如何使用低代码实现界面布局

HarmonyOS如何使用低代码实现界面布局

介绍 本篇Codelab是基于ArkTS语言的低代码开发方式实现的一个简单实例。具体实现功能如下&#xff1a; 创建一个低代码工程。通过拖拽的方式实现任务列表和任务信息界面的界面布局。在UI编辑界面实现数据动态渲染和事件的绑定。 最终实现效果如下&#xff1a; 相关概念 低代…
阅读更多...
ECharts5 概念篇2

ECharts5 概念篇2

数据转换 数据转换基础使用 在 echarts 中&#xff0c;数据转换是依托于数据集&#xff08;dataset&#xff09;来实现的. 我们可以设置 dataset.transform 来表示&#xff0c;此 dataset 的数据&#xff0c;来自于此 transform 的结果。下面是上述例子的效果&#xff0c;三个饼…
阅读更多...
冶炼金属（二分）

冶炼金属（二分）

题目描述&#xff1a; 小蓝有一个神奇的炉子用于将普通金属 O 冶炼成为一种特殊金属 X。 这个炉子有一个称作转换率的属性 V&#xff0c;V是一个正整数&#xff0c;这意味着消耗 V个普通金属 O 恰好可以冶炼出一个特殊金属 X&#xff0c;当普通金属 O 的数目不足 V 时&#x…
阅读更多...
【机器学习】基于粒子群算法优化的BP神经网络分类预测（PSO-BP）

【机器学习】基于粒子群算法优化的BP神经网络分类预测（PSO-BP）

目录 1.原理与思路2.设计与实现3.结果预测4.代码获取 1.原理与思路 【智能算法应用】智能算法优化BP神经网络思路【智能算法】粒子群算法&#xff08;PSO&#xff09;原理及实现 2.设计与实现 数据集&#xff1a; 多输入多输出&#xff1a;样本特征24&#xff0c;标签类别4…
阅读更多...
项目五 实现对学生信息的简单查询

项目五 实现对学生信息的简单查询

项目五 实现对学生信息的简单查询 1&#xff0c;查询数据库中部分字段的信息 使用select语句对表的选择及连接等操作&#xff0c;结构会生成一个临时表&#xff0c;将select结果存放到临时表中 查询数据表中所有字段的值 #格式&#xff1a;(*:表示所有列) select * from 表…
阅读更多...
milvus安装

milvus安装

milvus安装 sudo curl -L “https://github.com/docker/compose/releases/download/1.29.2/docker-compose- $ (uname -s)- $ (uname -m)” -o /usr/local/bin/docker-compose sudo chmod x /usr/local/bin/docker-compose sudo ln -s /usr/local/bin/docker-compose /usr/bin/…
阅读更多...
SpringBoot项目通过触发器调度实现定时任务

SpringBoot项目通过触发器调度实现定时任务

文章目录 前言一、quartz是什么&#xff1f;二、quartz中核心概念三、集成步骤1.引入依赖2.demo样例a.定义一个任务参数实体类b.定义操作触发器、定时任务接口及实现c.作业实现d.结果截图 四、其他1.QuartzJobBean和Job区别2.注意事项3.作业&#xff08;Job&#xff09;和触发器…
阅读更多...
考虑功率均分与电压频率的事件触发分布式二次控制MATLAB模型

考虑功率均分与电压频率的事件触发分布式二次控制MATLAB模型

微❤关注“电气仔推送”获得资料&#xff08;专享优惠&#xff09; 模型简介 此模型是在《基于事件触发机制的孤岛微电网二次电压与频率协同控制MATLAB仿真模型》上进一步创作的&#xff0c;之前的模型只考虑了二次电压与频率控制&#xff0c;并没有考虑均分这一项点。 因此…
阅读更多...
STM32相关资料汇总

STM32相关资料汇总

STM32选型表 STM32手册参考网站 https://www.stmcu.org.cn/
阅读更多...
文件包含漏洞之包含NGINX日志文件（常用）

文件包含漏洞之包含NGINX日志文件（常用）

条件&#xff1a;知道目标服务器的日志文件存贮路径&#xff0c;并且存在文件包含漏洞 首先对目标服务器发送一次含有木马的请求&#xff0c;目的是让目标服务器日志中生成含有木马的日志记录。因为发送过程中&#xff0c;使用了url编码&#xff0c;我们抓包进行更改成能够执行…
阅读更多...
网络——入门基础

网络——入门基础

目录 协议 网络协议 OSI七层模型 网络传输基本流程 网络传输流程图 局域网通信 数据包的封装和解包 广域网通信 网络地址管理 IP地址 MAC地址 协议 关于什么是局域网&#xff0c;什么是广域网&#xff0c;我这里就不过多赘述了&#xff0c;我们直接来谈一下什么…
阅读更多...
复旦发布层次性奖励学习框架，增强大模型人类偏好对齐

复旦发布层次性奖励学习框架，增强大模型人类偏好对齐

在人工智能领域&#xff0c;强化学习&#xff08;Reinforcement Learning, RL&#xff09;一直是实现智能体自主学习的关键技术之一。通过与环境的交互&#xff0c;智能体能够自我优化其行为策略&#xff0c;以获得更多的奖励。然而&#xff0c;当涉及到复杂的人类偏好时&#…
阅读更多...
codeforces 1600分

codeforces 1600分

文章目录 1.[G. Special Permutation](https://codeforces.com/problemset/problem/1352/G)2.[D. Constructing the Array](https://codeforces.com/problemset/problem/1353/D)3.[C2. k-LCM (hard version)](https://codeforces.com/problemset/problem/1497/C2)4.[C. Circle …
阅读更多...
【ollama】linux、window系统更改模型存放位置，全网首发2024！

【ollama】linux、window系统更改模型存放位置，全网首发2024！

首先是window系统 so easy 直接进入系统环境变量添加就行 其次是linux系统 全靠自己试出来的&#xff0c;去Ollama官网找半天文档不知道在哪&#xff0c;而且linux也没有说&#xff1a;【 https://github.com/ollama/ollama/blob/main/docs/README.md https://github.com/o…
阅读更多...
CSS Module

CSS Module

CSS Module的作用&#xff1a;将CSS样式作用域限制在特定的组件范围内&#xff0c;以避免全局样式污染和命名冲突。 Vue中如何实现样式模块…
阅读更多...
一款博客网站源码

一款博客网站源码

一款博客网站源码 源码软件库 为大家内置了主题 清爽又强大真正的永久可用的一条源码&#xff0c;该版本为整合版本&#xff0c;内置了Joe主题&#xff0c;搭建后直接启用即可~ 安装环境要求&#xff1a; PHP 7.2 以上 MySQL, PostgreSQL, SQLite 任意一种数据库支持&#xff…
阅读更多...
BUUCTF-WEB1

BUUCTF-WEB1

[ACTF2020 新生赛]Exec1 1.打开靶机 是一个ping命令 2.利用管道符“|” ping一下本地主机并查看ls ping 127.0.0.1 | ls 可以看到回显的内容是一个文件 127.0.0.1 | cat index.php #查看主机下index.php 127.0.0.1 | ls / #查看主机根目录下的文件 看的一个flag文件 …
阅读更多...
专升本 C语言 万字考点笔记全国通用

专升本 C语言 万字考点笔记全国通用

前言 全章内容多次校验整理,可以放心食用;如果发现内容有不严谨的地方,请随时私信张三xy 形而上学者谓之道&#xff0c;形而下学者谓之器 目录 前言 常考概念 一、C语言的基础知识 第一节、对C语言的基础认识 第二节、C语言程序生命周期 第三节、标识符 第四节、进制的转…
阅读更多...
帆软笔记整理

帆软笔记整理

一&#xff1a;表格值自定义显示 1、日期型格式化&#xff1a;FORMAT($$$,"MM月dd日") 或者&#xff1a; 2、普通值自定义显示&#xff1a;if($$$SW_1,丝网一号机,if($$$SW_2,丝网二号机,丝网三号机)) 或者&#xff1a; 二&#xff1a;从数据集中再次筛选&#…
阅读更多...
Wireshare捕获接口中没有本地连接

Wireshare捕获接口中没有本地连接

1. 查看npf服务是否启动 服务名无效&#xff0c;需要安转WinPcap 2. 勾选Npcap Packet Driver (NPCAP) 3. 重新启动Wireshark 重新启动Wireshark后&#xff0c;本地连接有了
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023