二郎最近在看定位算法，里面大家提到的比较多的就是加权最小二乘法，而也会提到闭式解，所以二郎带大家一起了解一下这些方法，希望大家都能懂得这个方法，而不是一看到就发懵。

1、闭式解=解析解
1）闭式解等价于解析解，可以把未知数提取出来（没有平方项、没有正弦余弦、没有幂项，单纯是一个变量）放到等号左边，把其他数据放在等号右边。能写成这样的形式，便可称之为闭式解。

这类方法的好处是无需估计和拟合，直接可以带入数据获得最终结果。

2、测量噪声
我们不管用什么设备对一个数据进行测量时，都会有误差。这里都会默认为我们的系统没有系统误差，只有随机误差，即误差符合高斯分布，均值为0（只有这样，我们才可以通过大量的测量，来消除误差对最终结果的影响，如果存在系统误差，它会往一个方向偏。）（什么？你不知道系统误差是啥？系统误差是一个系统的固有偏差，一般噪声是随机的，而偏差是固定的，平均值不为0）

这里我们拿TDOA算法为例子，在求解TDOA时，我们比较关注每次测量的距离差的噪声。

这里的ni1就是我们第i次测距和第1次测距之差的测量误差。

3、测量噪声的方差
方差是一种统计量，用于衡量数据集的离散程度或波动性。方差的计算通常涉及对一组数据进行统计分析，其中包括了多次测量的结果。
然而，在我们实际应用中，尤其是像加权最小二乘这样，我们很多情况下都是先写下测量误差，然后计算方差，而没有去说，多次测量，然后计算方差。

这里涉及到一个问题，方差的获取确实是需要多次测量，进而知道系统的性能。然后在使用中，尤其是在卡尔曼滤波中，这些方式都是被当作已知量，被直接应用，这里需要注意一下。

4、测量噪声的协方差矩阵
咱们先来说方差

这里的x是E（xi），即xi的期望，期望值是随机变量的加权平均值。通常情况下，我们的xi是多次测量的结果，即不存在权重，因此这里的期望是求均值。每个数与均值做差，然后求平方，这样就避免了正负号的问题，能直观地反映出每个数与均值地差距，即对同一目标进行一组测量，得到结果的离散程度。
这里我们也可以看到，方差也是求了平均，因此，很多时候这里的平均也写作E（（xi-x）^2）

现在来看协方差矩阵

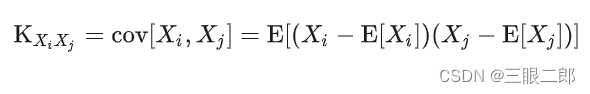
协方差矩阵表示不同变量之间的相关性，即一个变量和均值的差增大了，另一个变量也会随之改变。如上式也可以看出，两个只要是同时为正或者负，均值就会一直为正直。两个不同时为正或者负，那么均值就可能是0了（数学家还挺聪明的，通过这个来表示一次观测中，不同量之间的关系。我们没有必要去画那些什么相关图，因为我们只要理解了这是前人的智慧就可以了。我们也可以这么做，比如我们想知道我们同时测量两个数，他们两个是不是有关系，就可以看看他们是不是同增同减）
（生活中我们也可以用，比如我们多次测我们刷牙的时间和我们吃饭的时间，然后看是不是同增的，以此来判断关系，是不是很有趣，二郎就是这么有趣）
好了，说回来，这里提到了“矩阵”一次，一提到这个，我们就会头大
不知道是干啥的。
我们可以这么理解，协方差放到矩阵里，这里就能代表所有协方差的关系了。然后可以把这个矩阵利用在各种地方以获得自己想要的结果（我们没必要头疼一些未被应用的理论，在我们应用时再关注）。
在定位的论文中，用Q代表协方差，如下式

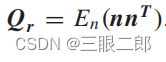
至此，我们已经知道什么是方差和协方差了，那么我们应该怎么用呢？？？

5、给出一个TDOA的例子，如何写误差

协方差矩阵如下

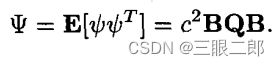
Q就是我们nnT

在实际使用中，我们会发现，我们可以得到测距方差（σ=10e-4），那么我们怎么获得我们的协方差？（这个是TDOA的，其他不一定适用，来自论文：A Simple and Efficient Estimator for Hyperbolic Location）

6、加权最小二乘法

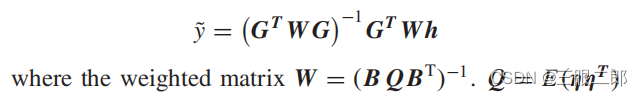
最小二乘法的权重就很好写了。不过这里也需要注意一点，很多时候我们没办法直接获得方差。
所以多数情况下，我们使用的加权最小二乘法，其实是迭代加权最小二乘法（IRLS）的一种变体。