很多人听到动态规划或者什么dp数组了，或者是做到一道关于动态规划的题目时，就会有一种他很难且不好解决的恐惧心理，但是如果我们从基础的题目开始深入挖掘动规思想，在后边遇到动态规划的难题时就迎难而解了。
 其实不然，动态规划类题目确实很不好发现解题思路，如何成为高手呢？那就是多刷题，但是还是像上边所说，不要刚接触就上难题只会让自己望而却步，我们只有不断积累经验，才能完全拿捏动态规划里面的精髓。
动态规划算法思想的核心
 有资料这样解释动态规划过程：
将问题分解为多个阶段，每个阶段对应一个决策，我们可以记录每个阶段所得到的状态的集合（去掉重复的），然后根据当前的状态的集合推导出下一阶段的状态集合，动态的向前推进，直至到达最终阶段，得到我们想要的结果。
有一位博主很巧妙地说明了上边所说的含义

A:问“1+1+1+1+1+1+1+1+1”等于几？
B:等于9

A:在表达式前边加上1+后结果等于几？
B:等于10（迅速）
A:为什么这么快得到结果呢？
B:因为我已经知道1+1+1+1+1+1+1+1+1等于9，再加1就得到10了
，而不是重新再算一遍。

 ok，了解了动态规划的思想，我们就可以来探寻遇到动态规划的问题时，我们应该怎么求解

首先，用一个简单的dp问题进行入门
第N个泰波那契数

在做每道题时，我们首先要来解析题目
 我们已经知道第0,1，2个数的值了，我们再来看后边的表达式，很明显，有了前边的值还有了这个表达式，我们可以求出任意n位置的值。
我们可以用动态规划的分析方法来分析这道题目

1. 状态表示
   我们可以创建一个数组
   
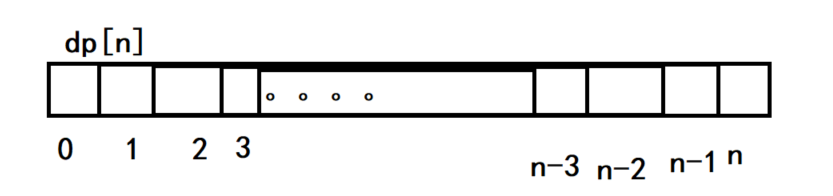
    这个数组就叫做dp表，我们所要做的就是把dp表中的数填满，然后就可以得到我们的最终结果。
    那么状态表示是什么意思呢？
    状态表示就是dp[i]位置上元素的含义，dp[i]在这道题目中就表示第i个泰波那契数的值。
    这道题目的状态表示很容易就能看出来，但遇到难题后，会遇到其他状态表示的方式，有一些会比较抽象，但是我们可以从浅入深，慢慢来嘛。

2. 状态转移方程
    这道题目的状态转移方程题目已经给出来咯，如果后边遇到某些题没给呢？那当然是自己找规律，很简单的。

dp[i]=dp[i-1]+dp[i-2]+dp[i-3];

3. 初始化
    如果知道了状态转移方程，然而不知道如何求出dp数组中的元素，那不就是没用嘛，所以前边给出我们前三个状态的值，由此我们才可以知道第四个，第五个的值。
    所以初始化还是很重要的，根据题目所示，将我们构建出的数组进行初始化。
4. 填表顺序
    这道题的填表顺序明显是从左到右，知道了前边数组的元素，我们才能根据状态转移方程来求解右边的值。
   你是怎么知道填表顺序的呢？
    确定填表顺序，为了填写当前状态表示的时候，所需要的状态已经计算过了。就像这道题，我们要求dp[4]的值，然而dp[3]我们都不知道，怎么求dp[4]呢？
5. 返回值
    根据状态表示，我们知道返回i位置的元素就是第i个泰波那契数，所以我们直接返回i即可
   现在我们就可以开始上手写代码
   写代码也是有几个步骤需要注意

class Solution {
public:
    int tribonacci(int n) {
        //创建dp表
        int* dp=new int[n+1];
        //边界问题
        if(n==0||n==1)
        {
            return n;
        }
        if(n==2)
        {
            return 1;
        }
        //初始化
        dp[0]=0;
        dp[1]=1;
        dp[2]=1;
        //填表
        for(int i=3;i<=n;i++)
        {
            dp[i]=dp[i-1]+dp[i-2]+dp[i-3];
        }
        return dp[n];
    }
};

6. 观察是否可以优化
   

 可以看出，我们内存消耗比较大，这是因为传入多少个n我们就开了n个空间，时间复杂度为O(N)，空间复杂度也是O(N)。
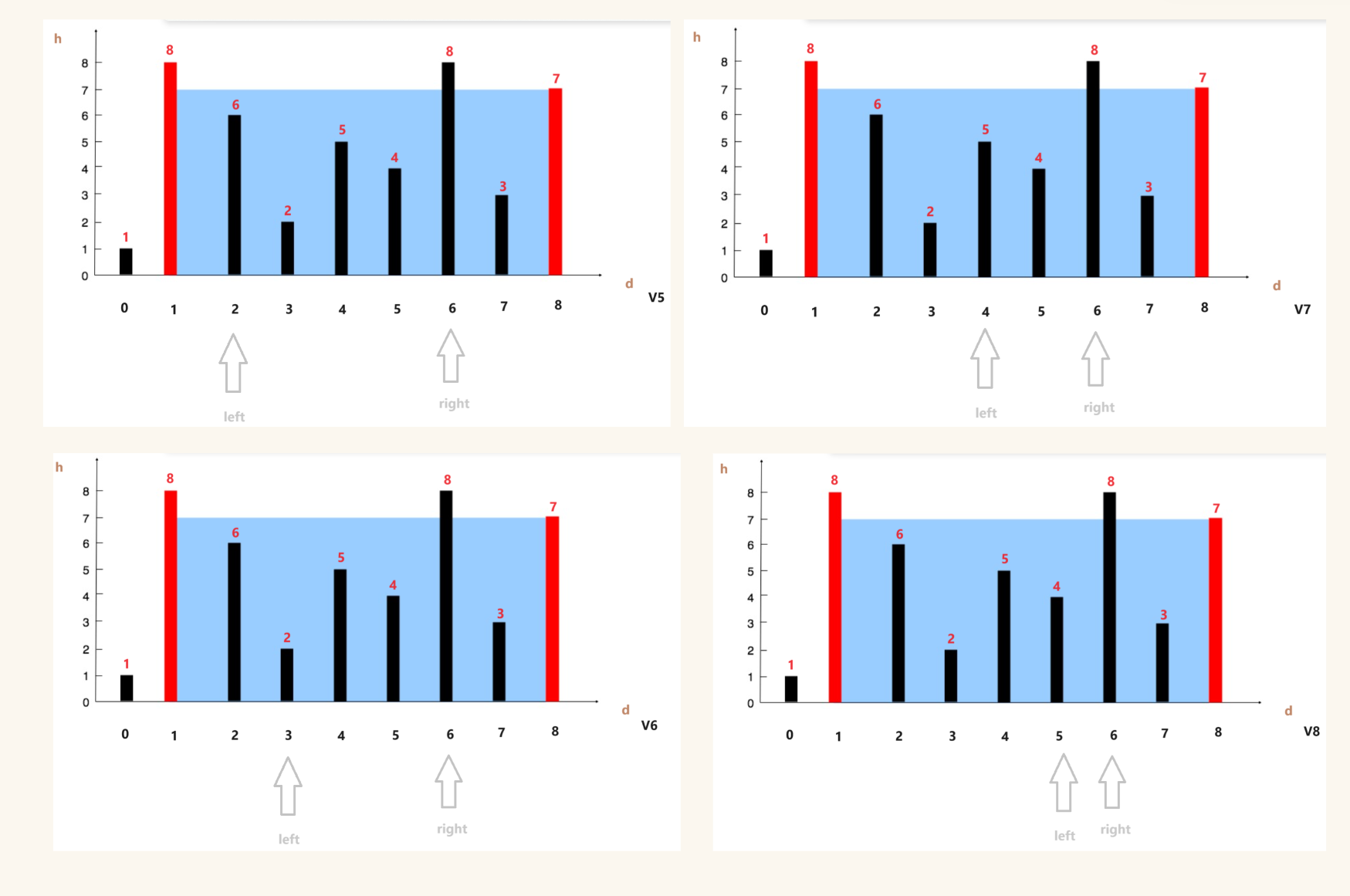
 这道题我们可以优化空间复杂度，我们在进行计算时，可以使用几个变量循环往复存储dp的值，这样只需要常熟级别的空间消耗就解决了这个问题。
如图

 然后我们就可以得出第四个结果的值为2，此时更新a,b,c中的值

优化后代码如下

class Solution {
public:
    int tribonacci(int n) {
        //创建dp表
        int a,b,c,sum;//定义四个变量
        //边界问题
        if(n==0||n==1)
        {
            return n;
        }
        if(n==2)
        {
            return 1;
        }
        //初始化
        a=0;
        b=1;
        c=1;
        //填表
        for(int i=3;i<=n;i++)
        {
            sum=a+b+c;
            a=b;
            b=c;
            c=sum;
        }
        return sum;
    }
};

 这道题我们会提到空间优化，后续中关于空间优化我们就不再多说了，重要的是能通过这道题，对吧！
接下来就是一道我们再熟悉不过的一种题目了，上楼梯问题
来看第一道关于上楼梯的题目
三步问题

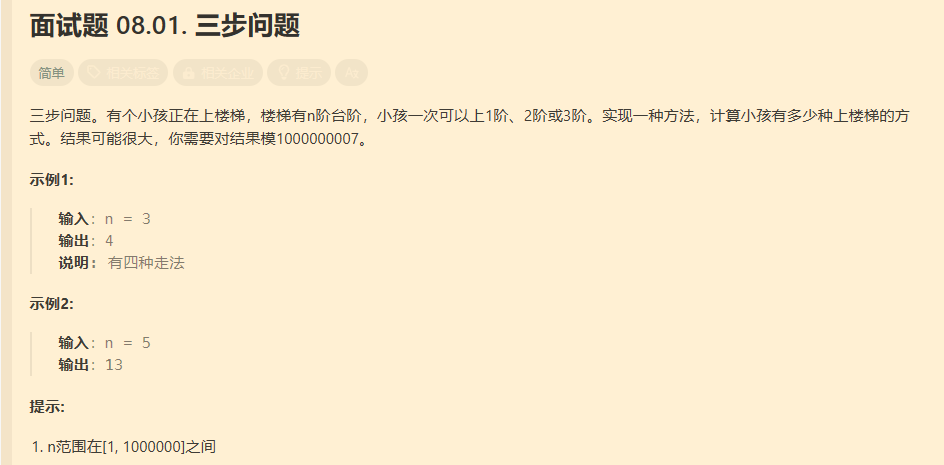
使用上边同样的分析步骤

1. 状态表示

 这道题目和上一道就已经截然不同了，我们需要自己进行分析，这道题目中，我们开出的dp表第i个位置的元素，表示的是到达第i位置台阶有多少种方法。

2. 状态转移方程

 小孩依次可以上1,2，3节台阶，我们可以一个一个进行分析，为什么这里状态表示是小孩到达该台阶所有的走法。

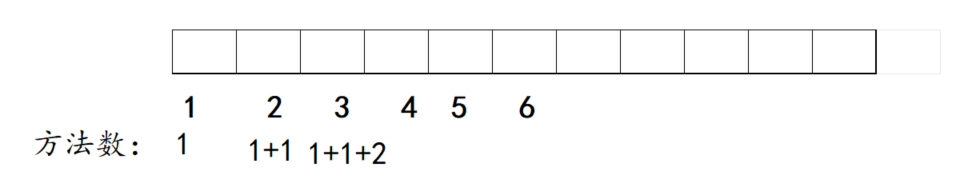
 小明上第一节台阶，显而易见，只有一种方法，就是直接跳上去.
 小明上第二个台阶时，我们就可以进行选择了，首先，我们可以先到第一个台阶，再从第一个台阶到第二个台阶，也可以直接到第二个台阶。
 怎么上第三个台阶呢？我们可以先到第一个台阶，再从第一个台阶直接到第三个台阶，到第一个台阶有一种方法，也可以先到第二个台阶，然后从第二个台阶到第三个台阶，到达第二个台阶有两种方法，所以到达第3个台阶有1+1+2中方法。

 从状态表示我们可以看出，小孩一次可以走三步，dp[i]就等于我们先到dp[i-1]的方法数量加上dp[i-2]加dp[i-3].
 所以状态表示方程为dp[i]=dp[i-1]+dp[i-2]+dp[i-3]
3. 初始化
 通过上边的分析，我们已经知道了爬前三节楼梯可以有的方法数目，不再赘述。

4. 确定填表顺序
    和前边拿到题目一样，填表顺序必须能帮助我们完成，在想要求出某个值时，所需要的元素都是已知的。
5. 返回值
    通过状态表示可以知道，返回dp[n]即返回到达第n节台阶时有多少种上楼梯的方法。

---

ok，有了上述的分析，我们就可以上手写代码了。

class Solution {
public:
    int waysToStep(int n) {
        //开dp表
        int* dp=new int[n+1];
        //边界调节
        if(n==1||n==2)
        {
            return n;
        }
        if(n==3)
        {
            return 4;
        }
        //初始化
        dp[1]=1;
        dp[2]=2;
        dp[3]=4;
        //填dp表
        for(int i=4;i<=n;i++)
        {
            dp[i]=dp[i-1]+dp[i-2]+dp[i-3];
        }
        return dp[n];
    }
};

运行后

 这个报错的含义就是计算结果超出了int的数据范围，这是因为我们忽略了题目中所说要对结果取模。

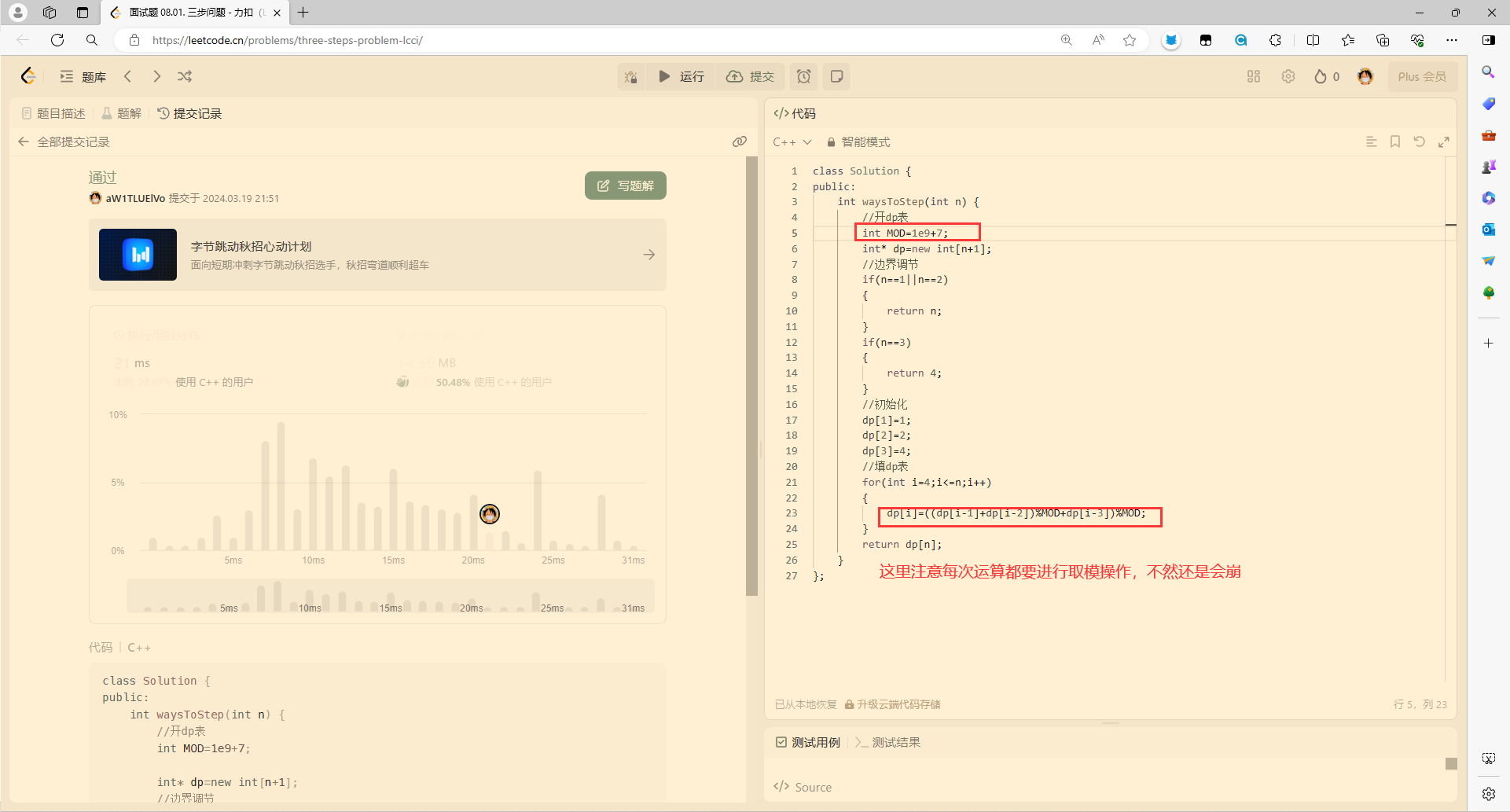
第三道题
使用最小花费爬楼梯

 这道题目还是一个爬楼梯的题目，一次可以爬两节，和上到题目不同的是，我们不需要计算方法数，而是在爬每节楼梯索要花费的最小花费，用同样的方法对象这道题目进行解析。
 但是这次我们可以选择从两个方面对这道题目进行分析

• 第一种

1. 状态表示

 有了上边的经验，这道题目我们同样可以知道，同样创建一个dp表，dp[i]表示到达i台阶花费的最少的money。
2. 状态转移方程
 我们一步一步进行分析，首先我们要知道cost第一个元素为台阶是0的台阶要花费的money，我们可以选择从第0个或者第1个台阶开始往上。 我们要想知道到达i位置所花费的最小数目，要到达第i阶只有两种方法，就是从第i-1位置或者第i-2位置往上跑过去的，所以我们要知道dp[i-1]加上第i-1位置的费用，还要知道dp[i-2]加上i-2台阶的费用。
所以我们的撞他转移方程为

dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])

3. 初始化
    初始化保证填表的时候不会越界。我们要到楼梯顶部，而cost数组是从0下标开始的，所以我们所要到达的楼顶是dp[n]，n就是cost的大小。
   这道题为什么没有边界判断呢？
    这是因为数据范围是大于等于2的。我们起始就在0或者1号台阶上，所以dp[0]=0,dp[1]=0.
4. 确定填表顺序
    我们想要知道爬到后边台阶花费的最少费用，就需要知道爬到他前边两个台阶所花费的最少费用加上从这个台阶向上爬所需要的费用。所以填表顺序是从左往右。
5. 返回值
    返回值就是dp[i]，i就是楼梯顶部需要的最低花费。要注意，顶楼并不是cost数组最后一个位置，cost最后的元素表示距离楼顶前的台阶往上爬所要消费的money。
   ok，接下来我们就可以上手写代码了。流程基本不变。

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int* dp=new int[cost.size()+1];
        dp[0]=0;
        dp[1]=0;
        for(int i=2;i<=cost.size();i++)
        {
            dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
        }
        return dp[cost.size()];
    }
};

---

接下来我们来换一种思路去求解这道题。

1. 状态表示
   dp[i]表示从i位置出发，到达楼顶需要的最少花费。和前边的思路不同的是，我们这次从前向后递进。
   

2. 状态转移方程
   
    很明显，我们应该选出两者之中小的那个，正如状态表示所说，dp[i]表示的是从该位置到达楼顶的最小花费。如果从i+1位置到达楼顶花费比从i+2位置到达楼顶花费少的话，我们当然要选择从i+1位置到达楼顶。
   状态转移方程为

dp[i]=min(dp[i+1]+cost[i],dp[i+2]+cost[i])

3. 初始化
    此时，根据状态方程，我们应该从右向左初始化，即初始化后边的值，dp表示从某位置出发到达楼顶位置，假设我们初始化的dp表为dp[n]。
   
    其中这里的n是cost.size()。表示的就是楼顶的位置，楼顶我们就不用初始化了，不管怎样都是0，dp[n-1]就是cost[cost.size()-1]。

4. 确定填表顺序
    填表顺序就是保证想要知道某位置的元素时，所需要的计算过程中的元素是已知的，所以这道题就是从右向左填表。

5. 返回值
    根据状态表示可知从i=0位置到达楼顶的花费和i=1位置到达楼顶的花费的较小值。
   代码如下

int minCostClimbingStairs(vector<int>& cost) {
        int* dp=new int[cost.size()+1];
        int n=cost.size();
        dp[n-1]=cost[n-1];
        dp[n-2]=cost[n-2];
        for(int i=n-3;i>=0;i--)
        {
            dp[i]=min(dp[i+1]+cost[i],dp[i+2]+cost[i]);
        }
        return min(dp[0],dp[1]);
    }