【算法与数据结构】深入二叉树实现超详解

news2024/11/24 16:30:00

请添加图片描述

文章目录

  • 📝前言
  • 🌠 接口函数
    • ✏️ 实现函数
      • 🌉创建树的新节点
      • 🌠通过前序遍历的数组构建二叉树
      • 🌉包装通过前序遍历的数组构建二叉树
      • 🌠二叉树的销毁
      • 🌠层次遍历
        • 🌠第一种实现：不用数组模拟队列
        • 🌠第二种实现：不用数组模拟队列，创建队列实现
      • 🌉判断二叉树是否是完全二叉树
      • 🌠二叉树节点个数
      • 🌉二叉树叶子节点个数
      • 🌉二叉树第k层节点个数
      • 🌠二叉树查找值为x的节点
    • 🌉 完整代码实现
    • 🌉测试一下效果
  • 🚩总结

📝前言

上节我们学习了二叉树（前中后）序遍历
这节将实现二叉树。

让我们复习一下二叉树，接着就是二叉树的实现了😊，学习起来吧！

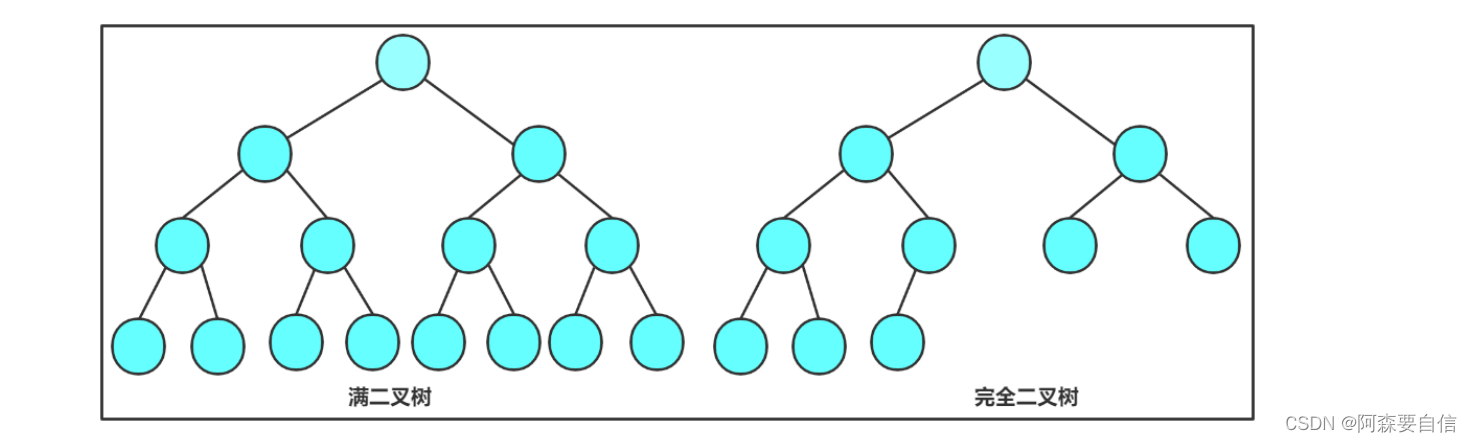
  1. 满二叉树：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为K，且结点总数是 ，则它就是满二叉树。
  2. 完全二叉树：完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
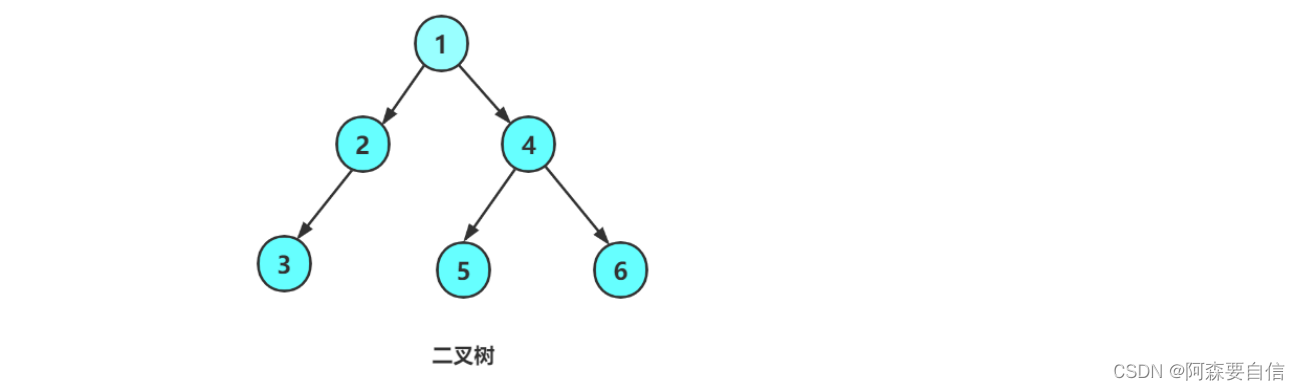
    在这里插入图片描述
    本节代码举例图
    在这里插入图片描述
    启动！—》

🌠 接口函数

头文件Tree.h，这里封装了树的接口，需要时直接#include"Tree.h"。

#include<stdio.h>
#include<stdlib.h>

# define _CRT_SECURE_NO_WARNINGS 1
//这里使用char是因为接下来测试用字符，
//当然你也可以改为别的类型哦
typedef char BTDataType;

// 二叉树节点结构
typedef struct BTNode {
    BTDataType data;
    struct BTNode* left;
    struct BTNode* right;
}BTNode;

//创建树的新节点
BTNode* BuyBTNode(int val);

//辅助函数：判断队列是否为空
int QueueIsEmpty(int front, int rear);


// 通过前序遍历的数组构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);

// 二叉树销毁
void BinaryTreeDestory(BTNode** root);

// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root);

// 二叉树节点个数
int BinaryTreeSize(BTNode* root);

// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);

// 层序遍历
void LevelOrder(BTNode* root);

✏️ 实现函数

🌉创建树的新节点

//创建新节点
BTNode* BuyBTNode(int val)
{
	//使用malloc动态申请内存,分配一个BTNode类型的结构体。
	BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));
	if (newNode == NULL)//
	{
		perror("malloc fail");//检查malloc是否成功
		return ;
	}
	newNode->data = val;//将新节点的data字段设置为传入的val值。
	newNode->left = NULL;//将新节点的left和right子节点指针设置为NULL。
	newNode->right = NULL;
	return newNode;//返回新创建的节点指针。
}

动态创建一个新的二叉树节点,并初始化其data和子节点指针字段。这样就可以在构建二叉树的过程中不断调用这个函数来创建新的节点,然后连接起来形成树形结构。

🌠通过前序遍历的数组构建二叉树

BTNode* BinaryTreeCreateHelper(BTDataType* a, int n, int* pi)
{									//n是数组a的长度
									//pi是索引指针,用于遍历a数组
	if (*pi >= n || a[*pi] == 'N')//检查*pi是否越界或当前元素为'N',如果是则跳过该节点,					(*pi)++向后移动。这里的N意思是空
	{
		(*pi)++;//
		return NULL;
	}
	//否则,调用BuyBTNode函数创建新的节点,并将a[*pi]的值赋给节点。(*pi)++后移。
	BTNode* newNode = BuyBTNode(a[(*pi)++]);
	if (newNode != NULL)
	{
		newNode->left = BinaryTreeCreateHelper(a, n, pi);//递归创建左子节点
		newNode->right = BinaryTreeCreateHelper(a, n, pi);//递归创建右子节点
	}

	return newNode;//每次递归都返回创建好的节点。

}

通过递归和索引下标的递增,就可以按先序遍历顺序依次创建二叉树的每个节点,并建立节点之间的父子关系，最终返回根节点,就完成了整个二叉树的创建。利用了递归的思想,通过不断调用自身函数来实现结构的生成。

BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{
	return BinaryTreeCreateHelper(a, n, pi);
}

🌉包装通过前序遍历的数组构建二叉树

BinaryTreeCreate函数是对BinaryTreeCreateHelper的一个包装。BinaryTreeCreateHelper负责具体创建二叉树的递归操作，BinaryTreeCreate作为入口函数,接收参数,调用辅助函数创建树,并返回根节点指针。

BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{
	return BinaryTreeCreateHelper(a, n, pi);
}

这样设计有利于函数单一职责原则,明确划分主函数和辅助函数的职责,更好地实现二叉树从先序序列的创建。

🌠二叉树的销毁

BinaryTreeDestory函数是用于释放二叉树占用的内存的。

void BinaryTreeDestory(BTNode** root)
{
	if (*root != NULL)
	{
		BinaryTreeDestory(&((*root)->left)); //释放左子树
		BinaryTreeDestory(&((*root)->right)); //释放右子树
		free(*root);//
		*root = NULL;
	}
}

🌠层次遍历

什么是层次遍历呢？
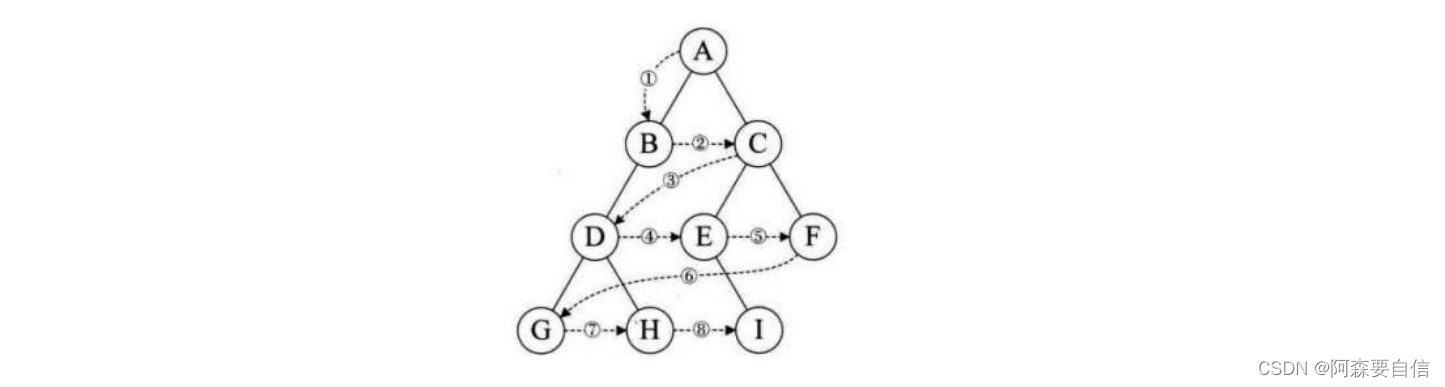
在这里插入图片描述
什么是层次遍历呢？我们先了解下层序遍历：除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。

So->

因此我们可以用队列控制，出队入队遍历二叉树

🌠第一种实现：不用数组模拟队列

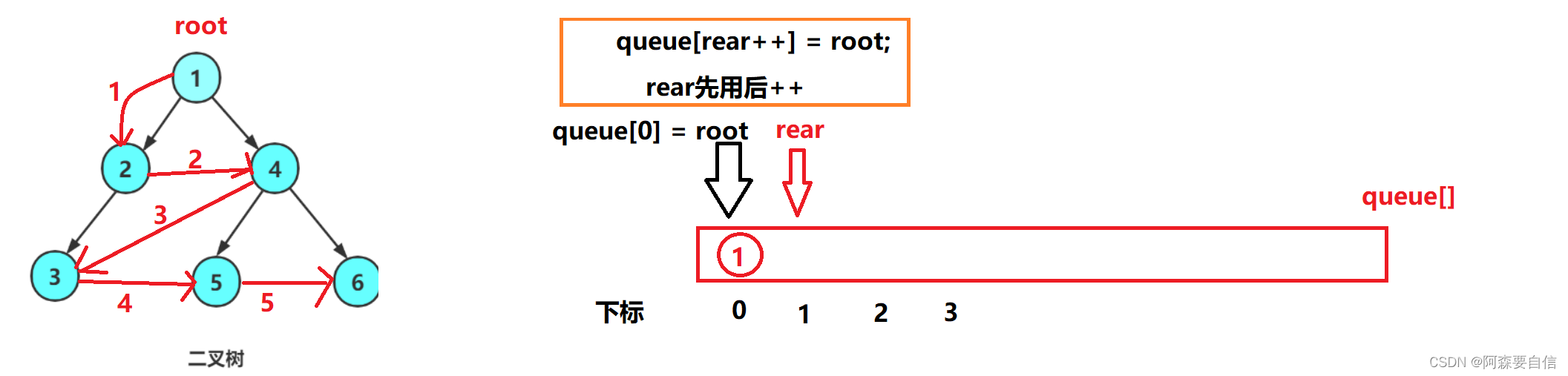
使用队列queue来模拟层序遍历,front和rear指针分别表示队头和队尾，front指针控制出队,rear指针控制入队,两个指针同时移动,就可以模拟出层序的遍历顺序。

void LevelOrder(BTNode* root) 
{
	if (root == NULL)//首先判断如果根节点为空,直接返回
		return;

	BTNode* queue[1000]; //使用队列queue来模拟层序遍历,front和rear指针分别表示队头和队尾
	int front = 0, rear = 0;
	queue[rear++] = root;//根节点入队

	while (front < rear) //循环结束时,front指针一定会等于rear指针,队列为空,遍历结束
	{											//关键是front指针每次递增1,实现队首出队
		BTNode* current = queue[front++];//取出队首节点current
		printf("%c ", current->data); 
		if (current->left != NULL)//如果当前节点有左子节点,将左子节点加入队尾
			queue[rear++] = current->left;
		if (current->right != NULL)//如果当前节点有右子节点,将右子节点加入队尾
			queue[rear++] = current->right;//rear指针每次递增1,实现节点入队
	}
}

在这里插入图片描述
在这里插入图片描述

🌠第二种实现：不用数组模拟队列，创建队列实现

void LevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);//初始化队列
	if (root)
		QueuePush(&q, root);//入队
	while (!QueueEmpty(&q))//判断是否为空
	{
		BTNode* front = QueueFront(&q);//取队头
		QueuePop(&q);//出队

		if (front)
		{
			printf("%d ", front->data);

			//带入下一层
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
		else
		{
			printf("N ");
		}
	}
	printf("\n");

	QueueDestroy(&q);//销毁队列
}

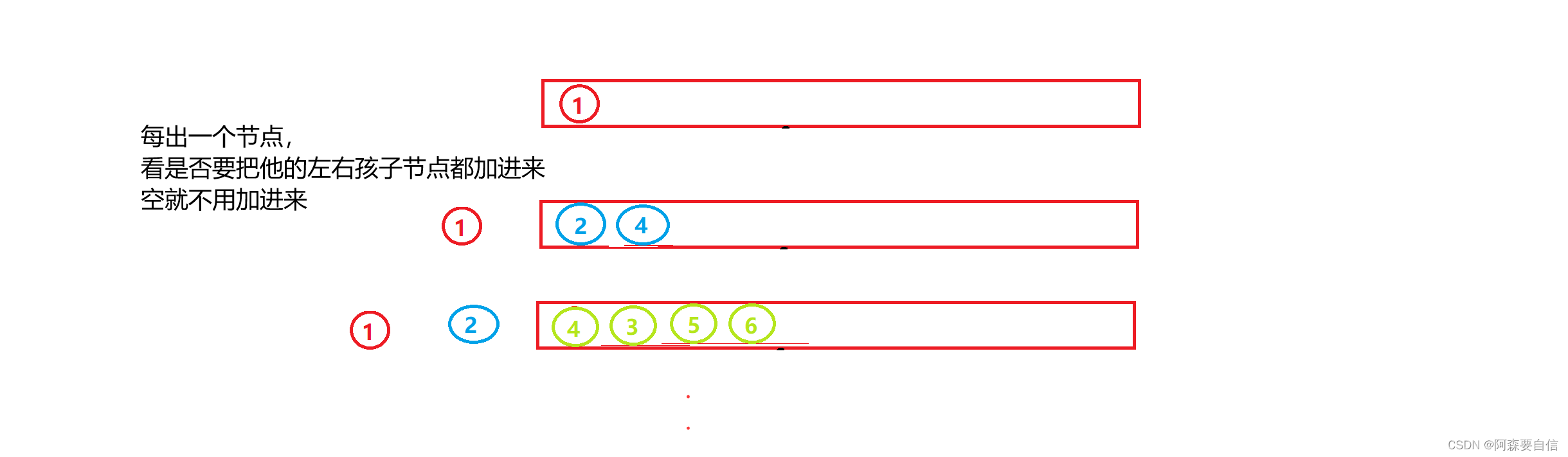
在这里插入图片描述

while循环条件是判断队列是否为空,不是front和rear指针比较。每次从队列取出节点front后,直接打印数据,然后入队其子节点。如果front为空,打印一个标识符"N"。

🌉判断二叉树是否是完全二叉树

在这里插入图片描述

//辅助函数：判断队列是否为空
int QueueIsEmpty(int front, int rear)
{
	return front == rear;
}

//判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root)
{
	if (root == NULL)
		return 1; //空树是完全二叉树

	BTNode* queue[1000];//用于存放节点的队列
	int front = 0, rear = 0;
	int flag = 0;//用于标记是否遇到空节点

	//根节点入队
	queue[rear++] = root;

	while (!QueueIsEmpty(front, rear))
	{
		BTNode* current = queue[front++];

		//如果遇到空节点后面还有非空节点，说明不是完全二叉树
		if (current == NULL)
			flag = 1;
		else
		{
			//左右孩子入队
			queue[rear++] = current->left;
			queue[rear++] = current->right;
			//如果遇到空节点后面还有非空节点，说明不是完全二叉树
			if (flag)
				return 0;
		}
	}

	//遍历结束，说明是完全二叉树
	return 1;
}

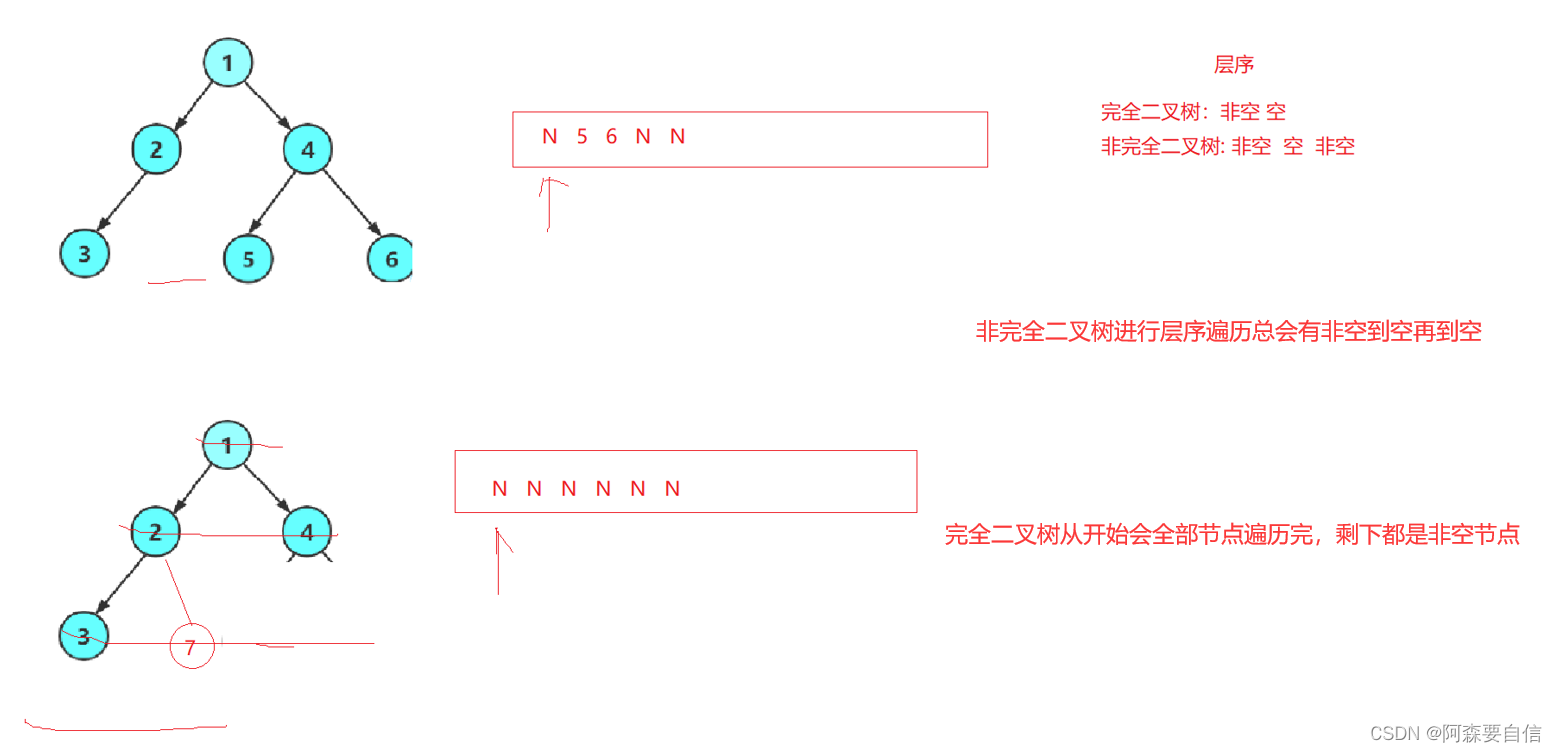
首先使用队列来层序遍历二叉树根节点入队，循环取出队首节点current，如果current为空,设置flag标记为1,表示遇到了空节点，如果current非空,将其左右孩子入队，如果flag已经被设置为1,说明之前遇到了空节点,现在又有非空节点,必然不是完全二叉树,直接返回0，遍历结束,说明没有发现flag为1后还有非空节点的情况,即树节点是从左到右依次完整填充每一层的,就是完全二叉树,返回1

🌠二叉树节点个数

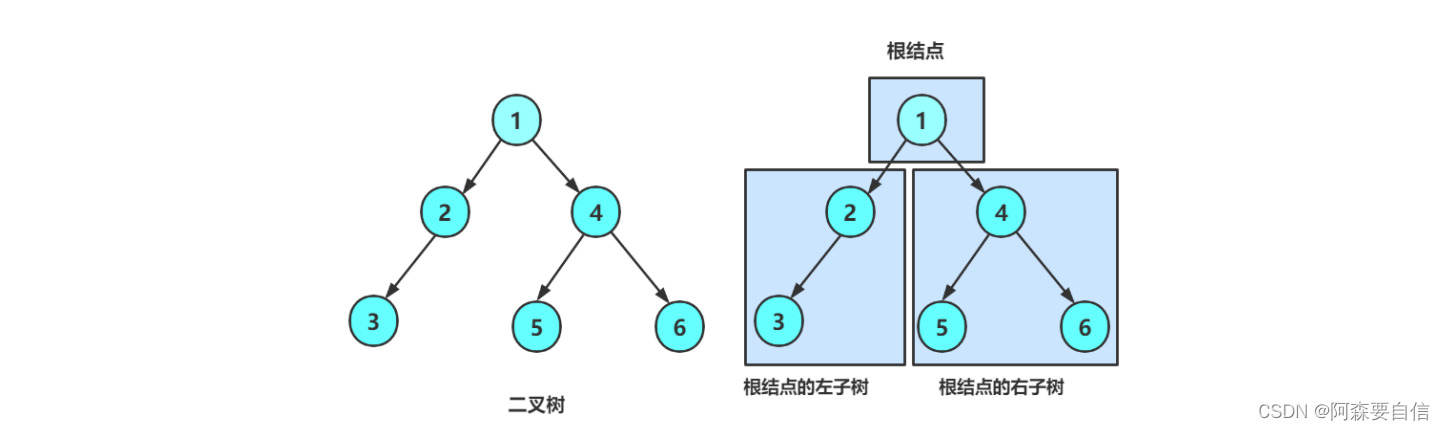
在这里插入图片描述

//二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
		return 0;//递归终止条件是空节点,返回0
	return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
	//非空节点返回它本身+左子树+右子树节点个数的和
}

这个函数BinaryTreeSize用来计算一棵二叉树的节点总个数。，如果传入的根节点root为空,说明这棵二叉树没有节点,返回0，如果不是空节点,则:这个节点本身就是1个节点，加上它左子树的节点个数BinaryTreeSize(root->left)，加上它右子树的节点个数BinaryTreeSize(root->right)，递归计算左右子树节点个数,然后汇总返回。时间复杂度为O(N),只需要一次遍历二叉树。

🌉二叉树叶子节点个数

//二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	if (root->left == NULL && root->right == NULL)
		return 1;//如果root节点的左右子节点都为空,则root就是叶子节点,返回1
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

如果传入的根节点root为空,说明这棵二叉树没有节点,返回0如果root节点的左右子节点都为空,则root就是叶子节点,返回1，否则:计算root的左子树叶子节点个数BinaryTreeLeafSize(root->left)，计算root的右子树叶子节点个数BinaryTreeLeafSize(root->right)
汇总返回左右子树叶子节点个数之和

🌉二叉树第k层节点个数

//二叉树滴k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
		//计算root的左子树第k-1层节点个数          //计算root的右子树第k-1层节点个数
	return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

递归基线是查询第一层或空树时返回值，每次递归都将层数k减1,向下查询下一层，从下至上不断累加各层节点个数，时间复杂度为O(N),只需要一次遍历。利用层序遍历思想实现对指定层的统计。

🌠二叉树查找值为x的节点

//二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)//根节点root为空,直接返回NULL
		return NULL;
	if (root->data == x)//root节点的数据等于查找值x,返回root
		return root;
	BTNode* leftResult = BinaryTreeFind(root->left, x);//在root的左子树中查找
	if (leftResult != NULL)//如果左子树找到返回结果,直接返回
		return leftResult;
	return BinaryTreeFind(root->right, x);//如果左子树没有找到,继续在root的右子树
}

递归终止条件是找到节点或者子树为空，先在左子树查找,如果找到直接返回，如果左子树没有找到,再在右子树查找，采用深度优先搜索的递归方式遍历整棵二叉树，时间复杂度为O(N),最坏情况需要遍历整棵二叉树。利用递归实现二叉树的深度优先搜索。

当然你也可以查找–>

// 查找x所在的节点
BTNode* TreeFind(BTNode* root, int x)
{
	if (root == NULL)//根节点root为空,直接返回NULL
		return NULL;

	if (root->val == x)//root节点的值等于x,返回root节点
		return root;

	BTNode* ret1 = TreeFind(root->left, x);
	//在root的左子树中查找TreeFind(root->left, x)
	if (ret1)//如果左子树找到节点,直接返回
		return ret1;
		
	//如果左子树没有找到,在root的右子树中查找TreeFind(root->right, x)/
	BTNode* ret2 = TreeFind(root->right, x);
	if (ret2)
		return ret2;

	return NULL;如果左右子树均没有找到,返回NULL
}

用深度优先搜索的递归方式遍历二叉树先在左子树查找，找到则返回,否则查右子树,递归终止条件是找到节点或者子树为空，时间复杂度为O(N),最坏情况需要遍历整棵树。

🌉 完整代码实现

#include<stdio.h>
#include<stdlib.h>
#include<tree.h>
typedef char BTDataType;

//二叉树节点结构
typedef struct BTNode
{
	BTDataType data;
	struct BTNode* left;
	struct BTNode* right;
}BTNode;

//创建新节点
BTNode* BuyBTNode(int val)
{
	BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));
	if (newNode != NULL)
	{
		newNode->data = val;
		newNode->left = NULL;
		newNode->right = NULL;
	}

	return newNode;
}

//辅助函数：判断队列是否为空
int QueueIsEmpty(int front, int rear)
{
	return front == rear;
}

//通过前序遍历的数组构建二叉树
BTNode* BinaryTreeCreateHelper(BTDataType* a, int n, int* pi)
{
	if (*pi >= n || a[*pi] == 'N')
	{
		(*pi)++;
		return NULL;
	}
	BTNode* newNode = BuyBTNode(a[(*pi)++]);
	if (newNode != NULL)
	{
		newNode->left = BinaryTreeCreateHelper(a, n, pi);
		newNode->right = BinaryTreeCreateHelper(a, n, pi);
	}

	return newNode;

}

BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{
	return BinaryTreeCreateHelper(a, n, pi);
}

//二叉树的销毁
void BinaryTreeDestory(BTNode** root)
{
	if (*root != NULL)
	{
		BinaryTreeDestory(&((*root)->left));
		BinaryTreeDestory(&((*root)->right));
		free(*root);
		*root = NULL;
	}
}

//判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root)
{
	if (root == NULL)
		return 1; //空树是完全二叉树

	BTNode* queue[1000];//用于存放节点的队列
	int front = 0, rear = 0;
	int flag = 0;//用于标记是否遇到空节点

	//根节点入队
	queue[rear++] = root;

	while (!QueueIsEmpty(front, rear))
	{
		BTNode* current = queue[front++];

		//如果遇到空节点后面还有非空节点，说明不是完全二叉树
		if (current == NULL)
			flag = 1;
		else
		{
			//左右孩子入队
			queue[rear++] = current->left;
			queue[rear++] = current->right;
			//如果遇到空节点后面还有非空节点，说明不是完全二叉树
			if (flag)
				return 0;
		}
	}

	//遍历结束，说明是完全二叉树
	return 1;
}

//二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}

//二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	if (root->left == NULL && root->right == NULL)
		return 1;
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}


//二叉树滴k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

//二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;
	if (root->data == x)
		return root;
	BTNode* leftResult = BinaryTreeFind(root->left, x);
	if (leftResult != NULL)
		return leftResult;
	return BinaryTreeFind(root->right, x);
}

//层序遍历
//void LevelOrder(BTNode* root)
//{
//	Queue q;
//	QueueInit(&q);
//	if (root)
//		QueuePush(&q, root);
//	while (!QueueEmpty(&q))
//	{
//		BTNode* front = QueueFront(&q);
//		QueuePop(&q);
//
//		if (front)
//		{
//			printf("%d ", front->data);
//
//			//带入下一层
//			QueuePush(&q, front->left);
//			QueuePush(&q, front->right);
//		}
//		else
//		{
//			printf("N ");
//		}
//	}
//	printf("\n");
//
//	QueueDestroy(&q);
//}


void LevelOrder(BTNode* root) 
{
	if (root == NULL)
		return;

	BTNode* queue[1000]; 
	int front = 0, rear = 0;
	queue[rear++] = root;

	while (front < rear) 
	{
		BTNode* current = queue[front++];
		printf("%c ", current->data); 
		if (current->left != NULL)
			queue[rear++] = current->left;
		if (current->right != NULL)
			queue[rear++] = current->right;
	}
}

🌉测试一下效果

int main()
{
	BTDataType preOrder[] = { '1','2','3','N','N','N','4','5','N','N','6','N','N' };
	int index = 0;
	BTNode* root = BinaryTreeCreate(preOrder, sizeof(preOrder) / sizeof(preOrder[0]), &index);

	printf("二叉树前序遍历结果为：");
		LevelOrder(root);
		printf("\n");
	
		printf("二叉树节点个数为:%d\n", BinaryTreeSize(root));
		printf("二叉树叶子节点个数为：%d\n", BinaryTreeSize(root));
		printf("二叉树第3层节点个数为：%d\n", BinaryTreeLevelKSize(root, 3));

		printf("二叉树是否是完全二叉树：%s\n", BinaryTreeComplete(root) ? "是" : "不是,换棵树看看~");

		BTNode* findNode = BinaryTreeFind(root, '3');
		if (findNode != NULL)
			printf("查找值为'3'的节点成功。\n");
		else
			printf("未找到该节点的值为3。\n");

		BinaryTreeDestory(&root);
		
		return 0;
}

代码前序构建图：
在这里插入图片描述
运行代码图
在这里插入图片描述

🚩总结

感谢你的收看，如果文章有错误，可以指出，我不胜感激，让我们一起学习交流，如果文章可以给你一个小小帮助，可以给博主点一个小小的赞😘，可以点点关注和赞哦 💓 💗 💕 💞
请添加图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1531629.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

如何在尽量不损害画质的前提下降低视频占内存大小?视频格式科普及无损压缩软件推荐

如何在尽量不损害画质的前提下降低视频占内存大小?视频格式科普及无损压缩软件推荐

大家好呀&#xff0c;相比大家都有对视频画质和体积的追求和取舍&#xff0c;那么&#xff0c;如何才能在不牺牲画质的前提下&#xff0c;尽可能的将视频大小降低到极致呢&#xff1f; 首先我们要了解视频的构成&#xff0c;要想降低视频的体积大小&#xff0c;我们可以从以下几…
阅读更多...
Learn OpenGL 22 高级光照与Gamma校正

Learn OpenGL 22 高级光照与Gamma校正

高级光照 Blinn-Phong 冯氏光照不仅对真实光照有很好的近似&#xff0c;而且性能也很高。但是它的镜面反射会在一些情况下出现问题&#xff0c;特别是物体反光度很低时&#xff0c;会导致大片&#xff08;粗糙的&#xff09;高光区域。下面这张图展示了当反光度为1.0时地板会…
阅读更多...
品牌方年度抖音店铺打造流量运营孵化方案

品牌方年度抖音店铺打造流量运营孵化方案

【干货资料持续更新&#xff0c;以防走丢】 品牌方年度抖音店铺打造流量运营孵化方案 部分资料预览 资料部分是网络整理&#xff0c;仅供学习参考。 PDF共120页&#xff08;完整资料包含以下内容&#xff09; 目录 抖音年度短视频直播运营规划方案 1. 帐号视频发布规划 问…
阅读更多...
55、服务攻防——数据库安全RedisHadoopMysql未授权访问RCE

55、服务攻防——数据库安全RedisHadoopMysql未授权访问RCE

文章目录 常见服务应用的安全测试&#xff1a; 配置不当——未授权访问安全机制——特定安全漏洞安全机制——弱口令爆破攻击 应用服务安全测试流程&#xff1a; 判断服务开放情况——端口扫描&组合猜解等 端口扫描&#xff1a;服务开放&#xff0c;绑定端口没开放&#…
阅读更多...
浅谈前端路由原理hash和history

浅谈前端路由原理hash和history

1、认识前端路由 本质 前端路由的本质&#xff0c;是监听 url 地址或 hash 值的改变&#xff0c;来切换渲染对应的页面组件 前端路由分为两种模式 hash 模式 history 模式 两种模式的对比 2、hash 模式 &#xff08;1&#xff09;hash 定义 hash 模式是一种把前端路由的路…
阅读更多...
管理类联考–复试–英文面试–问题--规划介绍原因做法--纯英文版

管理类联考–复试–英文面试–问题--规划介绍原因做法--纯英文版

借鉴 https://www.bilibili.com/video/BV1Dk4y187zN/?p4&spm_id_from333.880.my_history.page.clickhttps://www.bilibili.com/video/BV1Dk4y187zN/?p4&spm_id_from333.880.my_history.page.click https://ttsreader.com/zh/https://ttsreader.com/zh/ 规划 视频版…
阅读更多...
MyBatis3源码深度解析(十七)MyBatis缓存(一)一级缓存和二级缓存的实现原理

MyBatis3源码深度解析(十七)MyBatis缓存(一)一级缓存和二级缓存的实现原理

文章目录 前言第六章 MyBatis缓存6.1 MyBatis缓存实现类6.2 MyBatis一级缓存实现原理6.2.1 一级缓存在查询时的使用6.2.2 一级缓存在更新时的清空 6.3 MyBatis二级缓存的实现原理6.3.1 实现的二级缓存的Executor类型6.3.2 二级缓存在查询时使用6.3.3 二级缓存在更新时清空 前言…
阅读更多...
Java基础 学习笔记八

Java基础 学习笔记八

控制语句 分支语句 switch switch语句完整格式 expression 中执行完必须是个值并且必须是 int 或者 枚举 或者 字符串类型break语句只要执行&#xff0c;switch就要结束default语句不是必须的&#xff0c;但是建议写上&#xff0c;这样程序更加健壮 switch(expression){//exp…
阅读更多...
浅谈 电脑和车的对比

浅谈 电脑和车的对比

https://www.zhihu.com/question/547115488 电脑CPU与汽车发动机有哪些相同点与不同点&#xff1f; - 知乎 就想机械硬盘一样 我们的技术可能达不到 但是我们可以弯道超车 比如长江存储的SSD可以取代 以前的机械硬盘
阅读更多...
如何基于香橙派AIpro开发AI推理应用

如何基于香橙派AIpro开发AI推理应用

简介 香橙派AIpro开发板采用昇腾AI技术路线&#xff0c;接口丰富且具有强大的可扩展性&#xff0c;提供8/20TOPS澎湃算力&#xff0c;可广泛使用于AI边缘计算、深度视觉学习及视频流AI分析、视频图像分析、自然语言处理等AI领域。通过昇腾CANN软件栈的AI编程接口&#xff0c;可…
阅读更多...
深度学习pytorch——统计属性（持续更新）

深度学习pytorch——统计属性（持续更新）

矩阵范数 vs 向量范数 向量范数 1-范数&#xff1a;所有元素的绝对值之和。 2-范数&#xff1a;所有元素的平方之和&#xff0c;在开根号。 p-范数&#xff1a;所有元素的绝对值的p次方之和&#xff0c;再求其1/p次方。 例&#xff1a;向量X[2, 3, -5, -7] &#xff0c;求向…
阅读更多...
深入理解Linux内核页表映射分页机制原理

深入理解Linux内核页表映射分页机制原理

深入理解Linux内核页表映射分页机制原理 前言 操作系统用于处理内存访问异常的入口操作系统的核心任务是对系统资源的管理&#xff0c;而重中之重的是对CPU和内存的管理。 为了使进程摆脱系统内存的制约&#xff0c;用户进程运行在虚拟内存之上&#xff0c;每个用户进程都拥…
阅读更多...
静态网络配置

静态网络配置

一、查看网络命令 1.命令行查看网络配置 1、查看ip\硬件设备-网卡 ifconfig -a ifconfig ens160 网卡名称 ip addr show ip addr show ens160 nmcli device show ens160 nmcli con up ens160 2、主机名称 hostname hostname hfj.huaxia.com 3、查看路由和网关 rou…
阅读更多...
(C++20) jthread中stop_token的基础使用

(C++20) jthread中stop_token的基础使用

(C20) jthread中stop_token的基础使用 文章目录 (C20) jthread中stop_token的基础使用C20 jthread使用方式循环判断条件变量condition_variable_any stop回调 std::stop_callbackEND C20 jthread std::jthread - cppreference.com std::stop_token - cppreference.com std::sto…
阅读更多...
springboot3以及上版本引入RocketMQTemplate显示could not be found.

springboot3以及上版本引入RocketMQTemplate显示could not be found.

1. 问题所在 springboot3以及上版本引入RocketMQTemplate显示could not be found&#xff1f; 在springboot3时&#xff0c;直接通过依赖来注入RocketMQTemplate会报错&#xff0c;会显示没有这个对象。 这是因为在Springboot3以前的版本&#xff0c;自动装配是通过读取所有jar…
阅读更多...
Docker容器化技术（docker-compose安装部署案例）

Docker容器化技术（docker-compose安装部署案例）

docker-compose编排工具 安装docker-compose [rootservice ~]# systemctl stop firewalld [rootservice ~]# setenforce 0 [rootservice ~]# systemctl start docker[rootservice ~]# wget https://github.com/docker/compose/releases/download/v2.5.0/docker-compose-linux-…
阅读更多...
xinput1_3.dll丢失如何修复，xinput1_3.dll的安装修复教程分享

xinput1_3.dll丢失如何修复，xinput1_3.dll的安装修复教程分享

在Windows操作系统环境下&#xff0c;我们经常会遇到一些错误提示&#xff0c;其中之一就是“找不到xinput13.dll”。由于xinput1_3.dll是微软DirectX SDK的一部分&#xff0c;主要用于支持游戏手柄和其他外部设备的输入功能&#xff0c;缺失这一动态链接库文件可能导致某些依赖…
阅读更多...
高顿咨询如何用国产CRM实现经验决策到数据决策的跨越

高顿咨询如何用国产CRM实现经验决策到数据决策的跨越

编者按 近日&#xff0c;Salesforce 移动应用在中国大陆苹果应用商店的下架&#xff0c;预示着今年CRM国产化替代即将迎来高潮。CRM作为距离业务最近的软件&#xff0c;被公认为是企业数字化转型、高质量发展的核心系统之一。“企业如何选择一款真正满足自身业务需求的本土化C…
阅读更多...
邮件客户端 Thunderbird 简单配置

邮件客户端 Thunderbird 简单配置

1. 基本情况介绍 原来使用的邮箱客户端是 Office 365 自带的 Outlook 365切换原因&#xff1a;新装电脑&#xff0c;发现原 Outlook 中的账号信息无法迁移&#xff0c;需要耗费大量时间手动配置邮箱使用的邮箱&#xff1a;微软 O365 邮箱、qq 邮箱、163 邮箱、公司私有邮箱 …
阅读更多...
stable diffusion webui ubuntu 安装

stable diffusion webui ubuntu 安装

1.git clone 下来 GitHub - AUTOMATIC1111/stable-diffusion-webui: Stable Diffusion web UIStable Diffusion web UI. Contribute to AUTOMATIC1111/stable-diffusion-webui development by creating an account on GitHub.https://github.com/AUTOMATIC1111/stable-diffus…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023