深度学习pytorch——统计属性（持续更新）

news2024/11/24 18:36:37

矩阵范数 vs 向量范数

向量范数

1-范数：所有元素的绝对值之和。

2-范数：所有元素的平方之和，在开根号。

p-范数：所有元素的绝对值的p次方之和，再求其1/p次方。

例：向量X=[2, 3, -5, -7] ，求向量的1-范数，2-范数。

a = torch.full([8],1.)
print("1-范数：",a.norm(1))    # tensor(8.)
print("2-范数：",a.norm(2))    # tensor(2.8284)

矩阵范数

1-范数：所有元素的绝对值之和。

2-范数：所有元素的平方之和，在开根号。

p-范数：所有元素的绝对值的p次方之和，再求其1/p次方。

b=tensor([[1., 1., 1., 1.], [1., 1., 1., 1.]])

c=tensor([[[1., 1.], [1., 1.]], [[1., 1.], [1., 1.]]])

print("1-范数：",b.norm(1),c.norm(1))  # tensor(8.) tensor(8.)
print("2-范数：",b.norm(2),c.norm(2))  # tensor(2.8284) tensor(2.8284)

在不同维度上求范数就是消除这个维度，比如我现在有一个shape为[3, 2, 2]的张量，如果我要在第一维度上求范数，最后结果的shape就变成了[2, 2]了，实行的操作就是对本维度上的元素进行求范数处理。比如我已知如下一个张量：

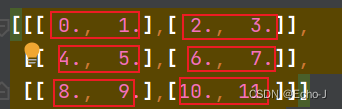
如果我在第0维度上求变量就是按红框中的元素进行处理：

最后的结果就是：[[12., 15.],[18., 21.]]。

如果我在第一维度进行求范数，就是对第一维度上的元素对应求范数，如下图所示：

最后的就是：[[ 2., 4.],[10., 12.],[18., 20.]]。

同理在第2维度求范数，就是在第二维度元素之间进行求范数操作：

结果就是：[[ 1., 5.], [ 9., 13.], [17., 21.]]。

均值、累加、最小值、最大值、累乘

这一类方法的实现都是先打平为1维的之后再求，最基本的用法就是tensorname.fun_name()：

min()       # 求最小值
max()       # 求最大值
mean()      # 求均值
prod()      # 求累乘
sum()      # 求累加
argmax()   # 求最大值的下标
argmin()   # 求最小值的下标

接下来讨论扩展的用法：

1、在特定维度上

a = tensor([[-1.5277, 0.3629, -1.2216, -1.3514, -0.7660, 0.0864, -0.9250, -0.6203,
0.1785, 1.0856],
[-0.3962, 0.6123, 0.3432, -2.0344, -0.5936, 0.9861, 1.2098, -1.0271,
0.5962, 1.5628],
[ 0.0584, -0.7316, -0.7060, 1.3894, -0.3185, 1.4347, 0.6946, -0.5441,
-2.1643, -0.3881],
[-0.2978, 0.7211, 1.1158, -1.6303, -0.7265, -0.1060, -1.2778, -0.0575,
-0.3458, -0.0525]])

print(a.max(dim=1))      # 在第一维度上最大值，并给出最大值所在的位置 torch.return_types.max(values=tensor([1.0856, 1.5628, 1.4347, 1.1158]),indices=tensor([9, 9, 5, 2]))
print(a.argmax(dim=1))   # tensor([9, 9, 5, 2])
print(a.max(dim=1,keepdim=True))  # keepdim是保持原来的维度，就是原来a是一个二维的张量，现在a也是个二维的张量，只是size改变了
print(a.argmax(dim=1,keepdim=True))

top-k

a.topk(3,dim=1)               # 求出a张量在一维上，前三大的元素
a.topk(3,dim=1,largest=False) # 求最小的三个
a.kthvalue(8,dim=1)           # 在第一维度上第八大的

比较

给定a1=tensor([[-0.1915, -0.1166, -0.3212],
[-1.4488, 0.9648, -2.3803],
[ 0.2105, 1.6176, 0.2730]])

1、使用运算符

这种情况就是将张量a中的每一个元素与0进行比较，如果大于零赋值为True，小于0赋值为False，最后返回一个3*3的张量，其它比较运算符同理，代码示例：

print(a1>0)

2、使用gt()方法

大于0的返回True，小于0的返回False，最后返回的是一个3*3的张量，代码示例：

print(torch.gt(a1,0))

3、使用eq()和equal()方法

a=torch.ones(2,3)
b=torch.randn(2,3)
 # 判断a和b是否相等，是一个元素一个元素进行对比，如果对应元素相等，则将对应的位置赋值为True，不等赋值为False，最后返回一个2*3的张量
print(torch.eq(a,b))
# 是直接判断两个张量是否相等，如果不相等直接返回一个False，相等则返回一个True   
print(torch.equal(a,b))

ccpytorch求范数函数——torch.norm - 慢行厚积 - 博客园 (cnblogs.com)https://www.cnblogs.com/wanghui-garcia/p/11266298.html#:~:text=pytorch%E6%B1%82%E8%8C%83%E6%95%B0%E5%87%BD%E6%95%B0%E2%80%94%E2%80%94torch.norm%201%20dim%20%28int%EF%BC%8C2-tuple%EF%BC%8C2-list%EF%BC%8C%20optional%29%3A%20%E6%8C%87%E5%AE%9A%E8%AE%A1%E7%AE%97%E7%9A%84%E7%BB%B4%E5%BA%A6%E3%80%82%20%E5%A6%82%E6%9E%9C%E6%98%AF%E4%B8%80%E4%B8%AA%E6%95%B4%E6%95%B0%E5%80%BC%EF%BC%8C%E5%90%91%E9%87%8F%E8%8C%83%E6%95%B0%E5%B0%86%E8%A2%AB%E8%AE%A1%E7%AE%97%EF%BC%9B%E5%A6%82%E6%9E%9C%E6%98%AF%E4%B8%80%E4%B8%AA%E5%A4%A7%E5%B0%8F%E4%B8%BA2%E7%9A%84%E5%85%83%E7%BB%84%EF%BC%8C%E7%9F%A9%E9%98%B5%E8%8C%83%E6%95%B0%E5%B0%86%E8%A2%AB%E8%AE%A1%E7%AE%97%EF%BC%9B%E5%A6%82%E6%9E%9C%E4%B8%BANone%EF%BC%8C%E5%BD%93%E8%BE%93%E5%85%A5tensor%E5%8F%AA%E6%9C%89%E4%B8%A4%E7%BB%B4%E6%97%B6%E7%9F%A9%E9%98%B5%E8%AE%A1%E7%AE%97%E7%9F%A9%E9%98%B5%E8%8C%83%E6%95%B0%EF%BC%9B%E5%BD%93%E8%BE%93%E5%85%A5%E5%8F%AA%E6%9C%89%E4%B8%80%E7%BB%B4%E6%97%B6%E5%88%99%E8%AE%A1%E7%AE%97%E5%90%91%E9%87%8F%E8%8C%83%E6%95%B0%E3%80%82%20...,3%20out%EF%BC%88Tensor%2C%20optional%EF%BC%89%3Atensor%E7%9A%84%E8%BE%93%E5%87%BA%E3%80%82%20%E5%A6%82%E6%9E%9Cdim%3DNone%E6%88%96out%3DNone%2C%E5%88%99%E5%BF%BD%E7%95%A5%E8%AF%A5%E5%8F%82%E6%95%B0%E3%80%82%204%20dtype%EF%BC%88torch.dtype%EF%BC%8Coptional%EF%BC%89%EF%BC%9A%E6%8C%87%E5%AE%9A%E8%BF%94%E5%9B%9Etensor%E7%9A%84%E6%9C%9F%E6%9C%9B%E6%95%B0%E6%8D%AE%E7%B1%BB%E5%9E%8B%E3%80%82%20%E5%A6%82%E6%9E%9C%E6%8C%87%E5%AE%9A%E4%BA%86%E8%AF%A5%E5%8F%82%E6%95%B0%EF%BC%8C%E5%9C%A8%E6%89%A7%E8%A1%8C%E8%AF%A5%E6%93%8D%E4%BD%9C%E6%97%B6%E8%BE%93%E5%85%A5tensor%E5%B0%86%E8%A2%AB%E8%BD%AC%E6%8D%A2%E6%88%90%20%3Aattr%3A%E2%80%99dtype%E2%80%99