2023年天府杯全国大学生数学建模竞赛
A题 震源属性识别模型构建与震级预测
原题再现:
地震是一种较为复杂的地壳运动现象,全世界每年发生的地震灾害事故不计其数。旨在减少地震灾害的地震预警预报技术需要在日常地震监测中有效识别出天然地震事件,剔除掉人工地震记录或异常干扰信号,然后进行后需操作。地震信号精准辨识是地震学研究和地震观测技术的重要内容,但随着城市工程建设项目的急剧增多和地震台网监测范围的扩大,爆破、矿震、武器试验、塌陷等非天然地震事件时有发生,干预了近震事件的记录、大震应急处置与地震目录的日常管理,有必要增强识别模型的可靠性与精度大小。
震级预测是地震预测的重要目标(震中、发震时间、震级等)之一,震级大小的精准判定依赖于大量历史事件的特征挖掘和地震波能量估计,且有助于开展针对性的地震应急方案制定,减少损失。
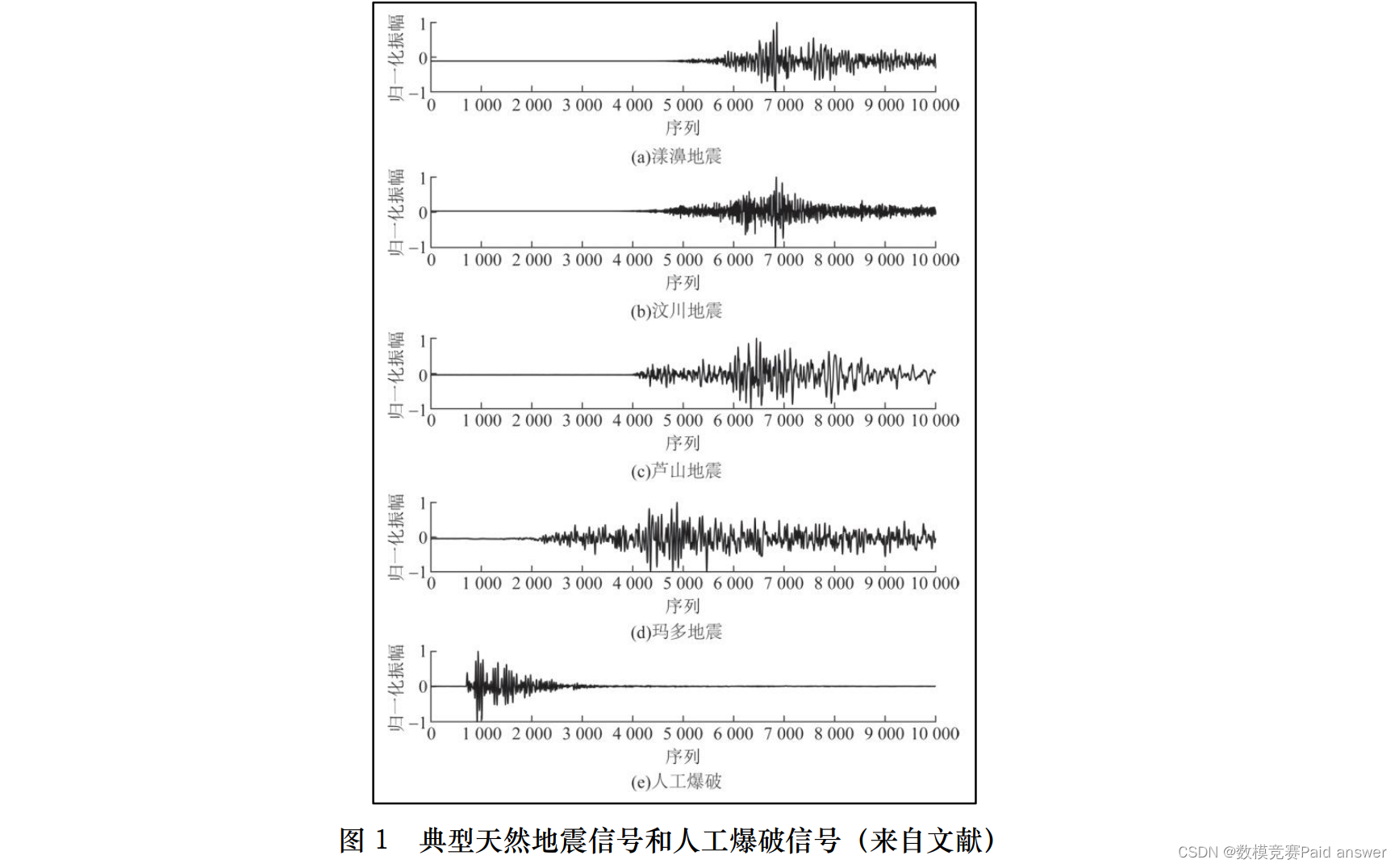
随着计算机技术和人工智能学科的发展,人工智能地震学应用而生,利用机器学习和神经网络模型解决常规地震学问题的手段亦逐渐取代传统方法,深入到震源属性识别模型构建与震级预测中。
请解决:
问题 1:针对附件 1~8 中的地震波数据,找出一系列合适的指标与判据,构建震源属性识别模型,进行天然地震事件(附件 1~7)与非天然地震事件(附件 8)的准确区分;
问题 2:地震波的振幅大小、波形特性与震级有着显著关联。根据已知震级大小的附件 1~7 中数据(震级大小分别为:4.2、5.0、6.0、6.4、7.0、7.4、8.0),恰当地挑选事件与样本,建立震级预测模型,尝试给出附件 9 中地震事件的准确震级(精确到小数点后一位)。
问题 3:库深、库容、断层类型、构造活动/基本烈度、岩性等是影响水库诱发地震震级大小的重要因素。请根据附件 10 中 102 个水库地震样本,尝试建立水库基本属性资料与震级的关系模型,并给出合理的依据。
注意:信号采样率统一为 200 Hz;附件 1~9 中每个附件皆代表一个独立地震事件,附件中的各个样本来自于同一地震事件中的不同台站观测数据,且数据物理含义相同(加速度或速度);库深单位为 m,库容单位为100000000m^3。
整体求解过程概述(摘要)
地震是一种复杂的地球现象,每年全球都会发生许多地震,因此寻找可靠的地震预警预报技术非常重要。为了能有效地识别出天然地震事件,并排除人为地震或其他信号的干扰,需要进行精确的地震信号辨识。同时,随着城市工程建设的增加和地震台网监测范围的扩大,非天然地震事件的发生也越来越多,因此增强模型的识别可靠性和精度也变得十分重要。在地震预测的众多目标之一,震级预测的精准判定有助于开展针对性的地震应急方案制定,减少灾害损失。
针对问题一,为了解决自然地震和非自然地震事件识别的问题,首先需要对所有站点收集到的数据进行合并处理。其次,利用MFCC方法对数据集进行特征提取。然后采用了多种分类器,包括概率神经网络、BP神经网络、支持向量机和logistic回归等,对数据进行二分类识别。最后,通过比较和分析结果,得出了附件9的具体类别为自然地震事件。
针对问题二,为了解决附件9的震级预测问题,首先利用问题一提取的特征数据,并通过主成分分析法进行数据降维,以减少数据维度,提高预测效果。利用灰色关联系数大致猜测附件9的震级值与附件4最为接近,即震级值为6左右。其次,建立了6种不同的预测模型,包括支持向量机回归、BP神经网络、模糊神经网络、多元线性回归模型,此外,还利用鮣鱼优化算法和增强版鮣鱼优化算法调整正则化系数,构建两种不同的岭回归模型对附件9的震级进行回归预测。最后,通过分析3种误差指标(平均绝对误差、均方根误差和平均百分比误差)以及拟合度R²,确定了较好的模型,并预测了附件9的震级值为6.1。
针对问题三,为了研究水库基本属性资料与震级之间的关系模型,首先,利用对“附件10”中的类别变量进行编码,便于后续建模分析。其次,运用建立岭回归模型,发现库容和库深与震级关系不显著,而岩性与震级的关系存在一定的争议,进一步通过逐步回归模型,选出影响因素的关键变量为断层类型和构造活动/基本烈度。然后,鉴于水库属性与震级之间可能存在非线性关系,应用增强版鮣鱼优化算法,建立了非线性回归模型,以更加准确地描述两者之间的关系。最后,进行模型误差对比和对自变量进行敏感性分析,确定最终的关系模型,即震级值关于断层类型和构造活动/基本烈度的非线性回归模型,其拟合度R²为0.981。
模型假设:
为了便于考虑问题,不影响模型准确性的前提下,作出以下假设:
(1)假设站台的测试数据能够反应震动类别。
(2)假设测试数据无误。
(3)对于震值的预测,假设站台测试数据能够反应震值。
(4)对于关系模型的建立,假设无其他强相关的变量影响震值。
问题分析:
针对问题一
为了解决识别自然地震和非自然地震事件的问题,首先,将所有站点收集的数据进行合并处理。其次,利用 MFCC 方法对数据集进行特征提取。然后,采用了多种分类器,包括概率神经网络、BP神经网络、支持向量机和logistic回归等,对数据进行了二分类识别。最后,通过比较和分析,确定了附件9的具体类别。
针对问题二
为了解决附件9的震级预测问题,首先,利用问题一提取的特征数据,并通过主成分分析法进行数据降维,以减少数据维度,提高预测效果。同时,利用灰色关联系数大致猜测附件9的震级值。然后,建立了6种不同的预测模型,包括支持向量机回归、BP神经网络、模糊神经网络、岭回归、线性回归模型等,对附件9的震级进行回归预测。最后,通过分析3种误差(平均绝对误差、均方根误差和平均百分比误差)和拟合度,得到较好的模型,并确定附件9的震级。
针对问题三
为了研究水库基本属性资料与震级之间的关系模型,首先,我们利用SPSSPRO对“附件10”中的类别变量进行编码,便于后续建模分析。其次,我们运用岭回归和逐步回归等统计方法,建立线性回归模型,并选出了影响因素的关键变量。鉴于水库属性与震级之间可能存在非线性关系,应用EROA,建立了非线性回归模型,以更加准确地描述两者之间的关系。最后,我们进行了误差比较和敏感性分析,以确定最终的关系模型。
模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
部分程序代码:(代码和文档not free)
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import animation
#定义计算区域
x0 = 0.0
x1 = 1.0
y0 = 0.0
y1 = 1.0
N = 100
ds = (x1 - x0)/N
t0 = 0.0
t1 = 1.4
M = 1400
dt = (t1 - t0)/M
x = np.linspace(x0, x1, N+1)
y = np.linspace(y0, y1, N+1)
t = np.linspace(t0, t1, M+1)
r = dt/ds;
#初始化计算区域
(X, Y, T) = np.meshgrid(x,y,t)
#解析解
uu = np.multiply(np.multiply(np.cos(np.sqrt(2) * np.pi * T),np.sin(np.pi * X)),np.sin(np.pi * Y))
#有限差分求解
#创建差分数组
u = np.zeros((N+1,N+1,M+1))
#加入初始条件1
for i in range(0,N+1):
for j in range(0,N+1):
u[i,j,0] = np.sin(np.pi*i*ds) * np.sin(np.pi*j*ds)
#加入初始条件2
for i in range(1,N):
for j in range(1,N):
u[i,j,1] = r**2 / 2 * (u[i+1,j,0] + u[i-1,j,0] + u[i,j+1,0] + u[i,j-1,0]) + (1 - 2*r**2) * u[i,j,0]
#加入边界条件
for k in range(0,M+1):
u[0,0,k] = u[0,N,k] = u[N,0,k] = u[N,N,k] = 0
#递推求[1,N-1]时刻波场
for k in range(1,M):
for i in range(1,N):
for j in range(1,N):
u[i,j,k+1] = r**2*(u[i+1,j,k]+u[i-1,j,k]+u[i,j+1,k]+u[i,j-1,k]) + (2-4*r**2)*u[i,j,k] -u[i,j,k-1]
(X, Y) = np.meshgrid(x,y)
t = 100
fig = plt.figure(figsize=(20,16))
ax1 = fig.add_subplot(131,projection='3d')
surf1 = ax1.plot_surface(X, Y, uu[:,:,t], cmap='viridis')
fig.colorbar(surf1)
ax1.set_xlabel('X Label')
ax1.set_ylabel('Y Label')
ax1.set_zlabel('Z Label')
ax1.set_title(f"analysis solution at time {t*dt}")
ax2 = fig.add_subplot(132,projection='3d')
surf2 = ax2.plot_surface(X, Y, u[:,:,t], cmap='viridis')
fig.colorbar(surf2)
ax2.set_xlabel('X Label')
ax2.set_ylabel('Y Label')
ax2.set_zlabel('Z Label')
ax2.set_title(f"FD solution at time {t*dt}")
ax3 = fig.add_subplot(133,projection='3d')
surf3 = ax3.plot_surface(X, Y, uu[:,:,t]-u[:,:,t], cmap='viridis')
fig.colorbar(surf3)
ax3.set_xlabel('X Label')
ax3.set_ylabel('Y Label')
ax3.set_zlabel('Z Label')
ax3.set_title(f"error at time {t*dt}")
plt.show()