目录

写在前面的话

一、机器学习的基本任务与方法分类

        机器学习的概念和定义

基本任务

二分类任务（Binary Classification）：

多分类任务（Multi-class Classification）：

多标签分类任务（Multi-label Classification）：

回归任务（Regression）：

方法分类

        监督学习

        非监督学习

        半监督学习

        增强学习

        批量学习与在线学习

        参数学习与非参数学习

        机器学习相关的“哲学”思考

二、部署安装基础运行环境

安装anaconda集成环境

安装pycharm编辑器

测试运行环境

jupter Notebook 的基础使用以及一些魔术方法

1. 基础使用：

2. 快捷键操作：

3. 常用魔法命令：

三、基础数据科学工具库

1. NumPy基础操作

2. NumPy数组的运算

3. Matplotlib基础

4. sklearn.datasets

四、最基础的分类算法kNN

1、欧拉距离

2、使用代码实现knn算法的实现过程

3、自行封装kNN邻近算法并测试

4、使用scikit-learn中的kNN

 5、仿照scikit-learn封装kNN

6、使用sklearn数据集测试封装的算法

7、输出结果分类的准确度

8、超参数和模型参数

9、网格搜索与kNN算法中更多的超参数

10、数据归一化 Featuer Scaling

最值归一化

均值方差归一化

最值归一化和均值方差归一化的区别

11、k近邻算法总结

五、线性回归算法

线性回归算法的概念和特点

分类问题和回归问题的区别

简单线性回归到多元线性回归

最小二乘法求解

梯度下降求解 

 衡量和评估模型的性能

MAE、MSE、RMSE的区别

六、梯度下降法

1、什么是梯度下降法

2、梯度下降法的数学公式

3、python实现梯度下降

4、 Python实现随机梯度下降法

七、主成分分析法PCA

PCA概念和特点

主成分分析法的数学公式

主成分分析和线性回归的区别

梯度上升法解决PCA问题

scikit-learn中的PCA

二维数据简单示例

 多维数据示例

使用PCA对数据特征进行降噪处理实践过程

对人脸识别数据集进行PCA 降维

八、多项式回归和模型泛化

多项式回归和线性回归的对比

过拟合和欠拟合

 模型的泛化和学习曲线

验证数据集与交叉验证 

偏差和方差

九、逻辑回归算法 

逻辑回归概念和特点

代码实现逻辑回归

逻辑回归的决策边界

 多类分类问题策略OvR与OvO

十、支撑向量机SVM

什么是SVM

 scikit-learn中的SVM实际使用

十一、决策树

什么是决策树 

信息熵和基尼系数

 sklearn.tree的简单使用示例

十二、集成学习

 什么是集成学习

Voting Classifier 和 Soft Voting Classifier 

Bagging 代码示例 

---

写在前面的话

通过本篇文章的学习，大家可以对机器学习这门学科的基本框架有一个初步的了解。

非常适合初识机器学习的小伙伴。

当然它也是人工智能、大模型、深度学习、神经网络、这些目前特别热且前沿的技术的基石。

在算法部分，每个经典算法都有具体实例代码演练，希望初次学习的小伙伴可以下载搭建基础的运行环境来实操一下，尤其是数字识别、人脸识别那一部分，还是很有趣味性的。

文章也会涉及到一些数学知识，如函数应用，因为机器学习很多算法的原理就是数学函数求解来的。所以学习机器学习，数学是根本绕不开的，不会推导数学函数的只需知道这个函数的具体作用即可。

还有就是文章篇幅字数都很长，阅读前可以先看一下目录，可以有一个初步的框架。

好了废话不多说，开启学习之旅吧。

一、机器学习的基本任务与方法分类

        机器学习的概念和定义

机器学习是一种人工智能（AI）的分支领域，旨在让计算机系统通过学习数据模式和规律，从而进行预测、分类、识别等任务，而无需明确地编程这些任务的规则。

具体来说，机器学习的过程通常包括以下几个步骤：

1. 数据收集：收集与问题相关的数据样本，这些数据样本包含了输入特征和对应的目标输出。数据可以来自各种来源，包括传感器、数据库、API等。

2. 数据预处理：对收集到的数据进行清洗、转换和规范化等预处理操作，以保证数据的质量和一致性。预处理包括处理缺失值、异常值、数据平滑、特征缩放等。

3. 特征工程：选择合适的特征，并进行特征提取、特征选择、特征变换等操作，以提高模型的性能和泛化能力。特征工程对机器学习模型至关重要，它直接影响到模型的表现和效果。

4. 选择模型：根据问题的性质和数据的特点选择合适的机器学习模型。常见的机器学习模型包括线性回归、逻辑回归、决策树、支持向量机、神经网络等。

5. 模型训练：使用训练数据集对选定的模型进行训练。训练过程中，模型通过学习数据样本的模式和规律来调整自身的参数，以最小化预测结果与真实标签之间的差异。

6. 模型评估：使用评估数据集对训练好的模型进行评估，以验证模型的性能和泛化能力。常用的评估指标包括准确率、精确率、召回率、F1分数、ROC曲线等。

7. 模型调优：根据评估结果对模型进行调优，包括调整超参数、改进特征工程、调整模型结构等操作，以提高模型的性能和泛化能力。

8. 模型部署：将训练好的模型部署到实际应用环境中，并与其他系统集成。在部署过程中需要考虑模型的性能、稳定性、安全性等因素。

综上所述，机器学习的核心目标是利用数据和算法构建模型，从而实现对未知数据的预测和分类。机器学习技术已经被广泛应用于各个领域，包括医疗、金融、电商、智能驾驶等，为人类提供了更加智能化的服务和决策支持。

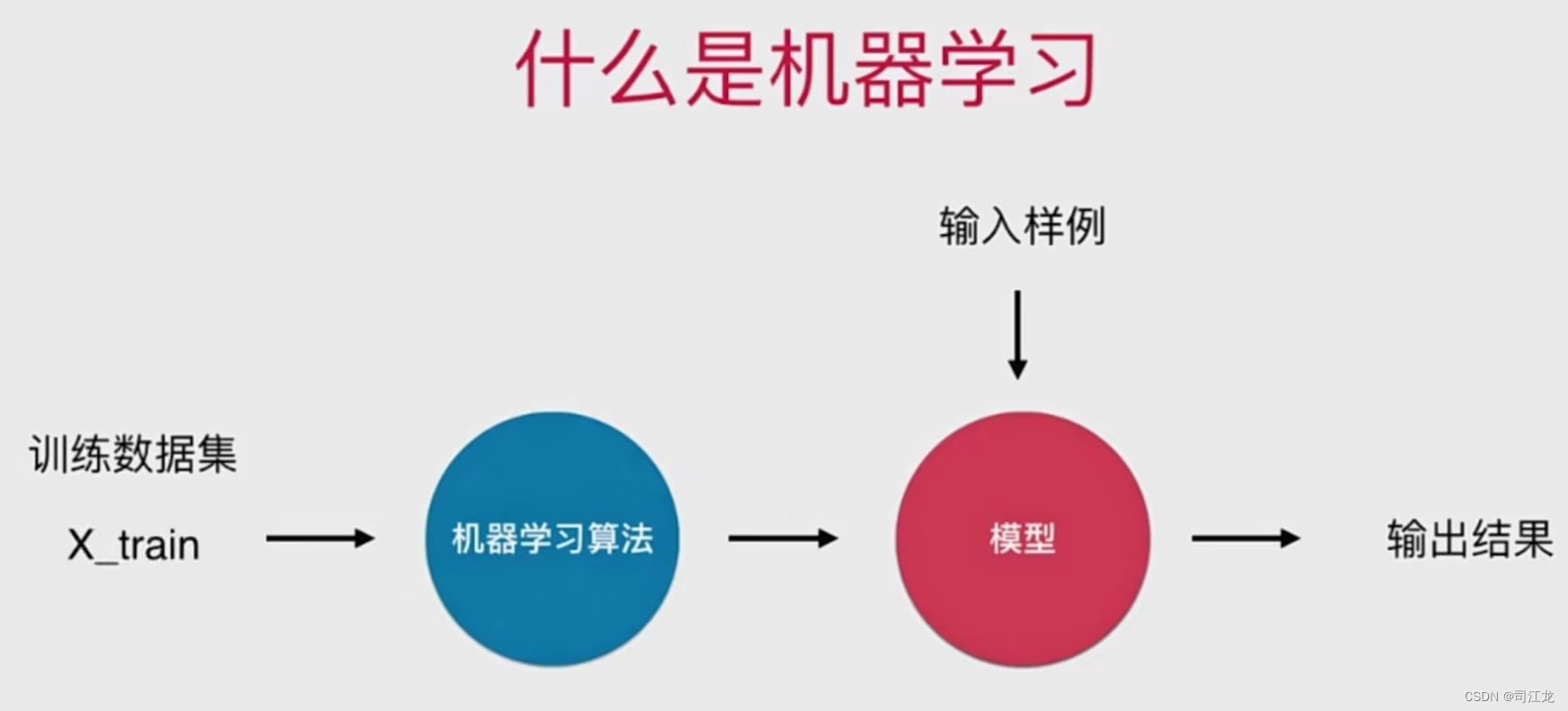
基本任务

机器学习的分类任务可以根据输出结果的类型和特点分为以下几类：

1. 二分类任务（Binary Classification）：

   • 特点：输出结果为两个类别之一，通常表示为正类（positive）和负类（negative）。
   • 示例：垃圾邮件识别、疾病诊断（是否患有某种疾病）、欺诈检测（是否存在欺诈行为）等。

2. 多分类任务（Multi-class Classification）：

   • 特点：输出结果为多个类别中的一个，可以是三个或三个以上的类别。
   • 示例：手写数字识别（数字0-9的识别）、图像分类（动物种类识别）、语音识别（语音指令识别）等。

3. 多标签分类任务（Multi-label Classification）：

   • 特点：每个样本可以属于多个类别，输出结果为多个二进制标签。
   • 示例：新闻主题分类（一篇新闻可以同时属于多个主题）、图像标签分类（一张图片可以包含多个物体）等。

4. 回归任务（Regression）：

   • 特点：输出结果是一个连续的数值。
   • 示例：房价预测、股票价格预测、销售额预测等。

方法分类

        监督学习

        概念：训练数据具有明确的标签或答案，机器学习算法通过这些标签来学习模式和关系，以便对新数据进行预测或分类。

        应用场景：广泛应用于分类和回归问题，如垃圾邮件分类、房价预测等。

        算法选择：根据数据类型和问题需求选择合适的监督学习算法，例如分类问题可选用逻辑回归、决策树等，回归问题可选用线性回归、多项式回归等。

        非监督学习

        概念：训练数据没有明确的标签，机器学习算法需要自行发现数据中的模式和结构，通常通过聚类等方法进行分析。

        应用场景：用于发现数据中的隐藏模式、聚类、降维等任务，如市场分析、用户分群等。

        算法选择：根据任务需求选择合适的非监督学习算法，例如K均值聚类、DBSCAN聚类、主成分分析（PCA）等。

        半监督学习

        概念：一部分数据拥有“标记”或者答案，另一部分数据没用有。

        应用场景：当标注数据成本高昂或难以获取时，半监督学习可以利用少量标记数据和大量未标记数据来提高模型性能。

        算法选择：半监督学习算法包括基于图的半监督学习、自训练、生成式模型等。

        增强学习

        概念：根据周围的环境情况，采取行为，根据采取行动的结果，学习行动方式。直白讲就是 一圈一圈的跑，不断的自动优化。监督学习和非监督学习是它的基础。

        应用场景：适用于需要在复杂环境中做出决策和行动的问题，例如智能游戏玩家、无人驾驶汽车等。

        算法选择：增强学习算法包括Q学习、策略梯度方法、深度强化学习等。

        批量学习与在线学习

        批量学习就是使用大量的数据资料生成固定的生产环境模型，优点是简单，缺点是没法适应环境的变化，一但变化需要重新跑大量的数据重新生成模型。

        在线学习就是每次生成模型的输入和输出结果都是训练的数据，缺点就是新的数据（不好、不准确的结果）有可能给模型带来不好的结果和影响，解决方案就是对数据进行监控。

        应用场景：批量学习适用于数据量较小、稳定的场景，而在线学习适用于数据量较大、动态变化的场景。

        算法选择：批量学习常用的算法有梯度下降、牛顿法等，而在线学习常用的算法有随机梯度下降、在线学习向量量化等。

        参数学习与非参数学习

        参数学习对模型做出一定假设，并学习这些假设的参数，例如线性回归、逻辑回归等。 一旦学到了参数，就不再需要原有的数据集

        非参数学习不对模型进行过多的假设，非参数不等于没参数，根据数据自行学习模型的复杂性，例如决策树、随机森林等。

        应用场景：参数学习通常用于对数据具有一定先验假设的情况，非参数学习则更适用于数据分布不确定的情况。

        算法选择：参数学习的算法有限，如线性回归、逻辑回归等，而非参数学习的算法更灵活，如决策树、随机森林等。

        机器学习相关的“哲学”思考

        机器学习主要处理一些不确定的一些问题，这和我们传统的一些经典算法不同，经典的算法都是有唯一固定的答案的，但是机器学习不同，它面对的是高度不确定的问题。数据和算法是提升机器学习能力的的两大因素。

        算法的选择：奥卡姆剃刀（简单的就是好的），脱离具体问题，谈哪个算法好是没用意义的，在面对一个具体问题的时候，尝试使用多种算法进行对比实验，是必要的。

        面对不确定的世界，怎么看待使用机器学习进行预测的结果？

二、部署安装基础运行环境

安装anaconda集成环境

Anaconda是一个用于科学计算的开源软件包管理器和环境管理器，它是Python和R编程语言的发行版，包含了数千个常用的Python和R软件包，以及数据科学和机器学习工具，如NumPy、Pandas、Matplotlib、Scikit-learn等。

允许用户创建多个独立的环境，每个环境可以有不同的Python版本和软件包集合，以满足不同项目的需求。

支持Windows、Linux和macOS等主流操作系统，用户可以在不同平台上使用相同的开发环境和工具。

Anaconda是一个功能强大的科学计算平台，它为用户提供了方便快捷的软件包管理和环境管理工具，使得Python和R编程变得更加简单和高效。

官方下载地址：https://www.anaconda.com/download

安装pycharm编辑器

官方下载地址：PyCharm：JetBrains为专业开发者提供的Python IDE

pycharm包含收费版和社区版，社区版是开源可以免费使用的

测试运行环境

import numpy
import matplotlib
import sklearn
import pandas

print("Hello Machine Learning!")

注意：如果运行报错依赖包找不到，检查pycharm的python解释器是否conda环境，如果不是需要添加conda环境的解释器，conda 自带了以上测试代码的依赖包，如果是系统环境或者其它，pip安装以上依赖包也是可以的。

jupter Notebook 的基础使用以及一些魔术方法

Jupyter Notebook是一个交互式的笔记本环境，支持多种编程语言，最常用的是Python。下面是关于Jupyter Notebook的基础使用以及一些常用的技巧和魔术命令：

1. 基础使用：

• 启动Jupyter Notebook：在命令行中输入jupyter notebook并回车，将会在默认浏览器中打开Jupyter Notebook的主界面。
• 创建新的Notebook：在主界面点击右上角的"New"按钮，选择要创建的Notebook类型（如Python、R等）。
• 执行代码：在代码单元格中输入代码，按Shift + Enter执行代码并移动到下一个单元格，按Ctrl + Enter执行代码并停留在当前单元格。
• 插入新的输入框：在菜单栏中选择"Insert" -> "Insert Cell Below"（在当前单元格下方插入新的单元格）或者"Insert" -> "Insert Cell Above"（在当前单元格上方插入新的单元格）。
• 删除单元格：选择要删除的单元格，点击菜单栏中的"Edit" -> "Delete Cells"或者按下键盘上的D键两次。

2. 快捷键操作：

• 运行单元格：Shift + Enter（执行并移动到下一个单元格）或者Ctrl + Enter（执行并保留在当前单元格）。
• 插入新的单元格：在命令模式下按A（在当前单元格上方插入）或者B（在当前单元格下方插入）。
• 删除单元格：在命令模式下按D两次。
• 切换单元格模式：在命令模式下按Y切换到代码模式，按M切换到Markdown模式。
• 保存Notebook：按Ctrl + S保存当前Notebook。

3. 常用魔法命令：

• %run：运行外部Python脚本。
• %timeit：测量代码执行时间。
• %matplotlib inline：在Notebook中显示Matplotlib图形。
• %reset：清除所有变量的名称空间。
• %%writefile：将单元格中的内容写入文件。
• %load：加载外部Python脚本或模块。
• %pwd：显示当前工作目录路径。
• %cd：更改当前工作目录。
• %ls：列出当前目录的文件和子目录。

三、基础数据科学工具库

在学习机器学习中我们需要Python中用于科学计算的一个重要工具包，它们提供了高效的相关操作函数。下面只是介绍了比较常用的和下面文章中用到的几个依赖包。

1. NumPy基础操作

NumPy是Python中用于科学计算的一个重要工具包，它提供了高效的多维数组对象和相应的操作函数。以下是一些基础操作：

• 创建数组和矩阵：使用np.array()函数创建数组，使用np.matrix()函数创建矩阵。
• 基本属性：数组的形状、维度、数据类型等属性。
• 数据访问：索引和切片操作访问数组中的元素。
• 合并与分隔：使用np.concatenate()和np.split()函数合并和分隔数组。
• 维度修改：使用np.reshape()函数修改数组的维度。

2. NumPy数组的运算

NumPy数组支持各种数学运算，包括向量和矩阵的运算、聚合运算、数学函数运算等。

• 数组运算：加减乘除、乘方、求余等。
• 数学函数运算：绝对值、正弦、余弦、正切、指数等数学函数运算。
• 矩阵运算：矩阵乘法、逆矩阵、伪逆矩阵等。

3. Matplotlib基础

Matplotlib是Python中用于绘制数据图表的库，常用于数据可视化。

• 绘制线图、散点图、柱状图等：使用plt.plot()、plt.scatter()、plt.bar()等函数进行绘制。
• 设置坐标轴、标题和标签：使用plt.xlabel()、plt.ylabel()、plt.title()等函数设置图表属性。
• 添加图例：使用plt.legend()函数添加图例以标识不同的数据系列。

4. sklearn.datasets

sklearn.datasets模块包含了一些常用的数据集，可以用于机器学习任务的训练和测试。

• 加载数据集：使用sklearn.datasets.load_*()函数加载对应的数据集。
• 查看数据集文档：通过查看相应函数的文档，了解数据集的属性、特征和标签等信息。

四、最基础的分类算法kNN

kNN邻近算法：两个（或者多个）特征的数据集，计算新的数据点邻近或者属于哪一类的特征数据集。

特点：适合入门机器学习、思想极度简单、应用数学知识少、可以解释机器学习算法使用过程中的很多细节问题、更完整的刻画机器学习应用流程。

1、欧拉距离

欧拉距离是一种用于衡量两个点之间的距离的方法，通常用于几何学和机器学习等领域。简单来说，欧拉距离表示两个点在空间中的直线距离，就像我们在地图上测量两个地点之间的直线距离一样。无论是在二维平面还是在更高维的空间都适用。

2、使用代码实现knn算法的实现过程

import numpy as np
import matplotlib.pyplot as plt
#查看raw_data_x原始数据集的特征点
aw_data_x = [[3.37086107,2.18526045],
             [3.55642876,1.72918867],
             [1.58794548,3.49198377],
             [3.38792636,4.91105222],
             [2.40416776,2.63642478],
             [7.40395068,4.65064059],
             [5.52275251,3.73818019],
             [9.79558531,2.72280788],
             [7.41003511,3.88750517],
             [7.3726532,0.62106226]]
raw_data_y = [0,0,0,0,0,1,1,1,1,1] #0为蓝色特征 1 为红色特征
x_train = np.array(raw_data_x)
y_train = np.array(raw_data_y)
plt.scatter(x_train[y_train==0,0],x_train[y_train==0,1],color='g')
plt.scatter(x_train[y_train==1,0],x_train[y_train==1,1],color='r')
plt.show() #得到以下特征散点图

x = np.array([8.09565541,3.52106226]) #又来了新的数据，判断是红色的一类还是绿色的一类
plt.scatter(x_train[y_train==0,0],x_train[y_train==0,1],color='g')
plt.scatter(x_train[y_train==1,0],x_train[y_train==1,1],color='r')
plt.scatter(x[0],x[1],color='b')
plt.show() #查看新的数据在散点图的位置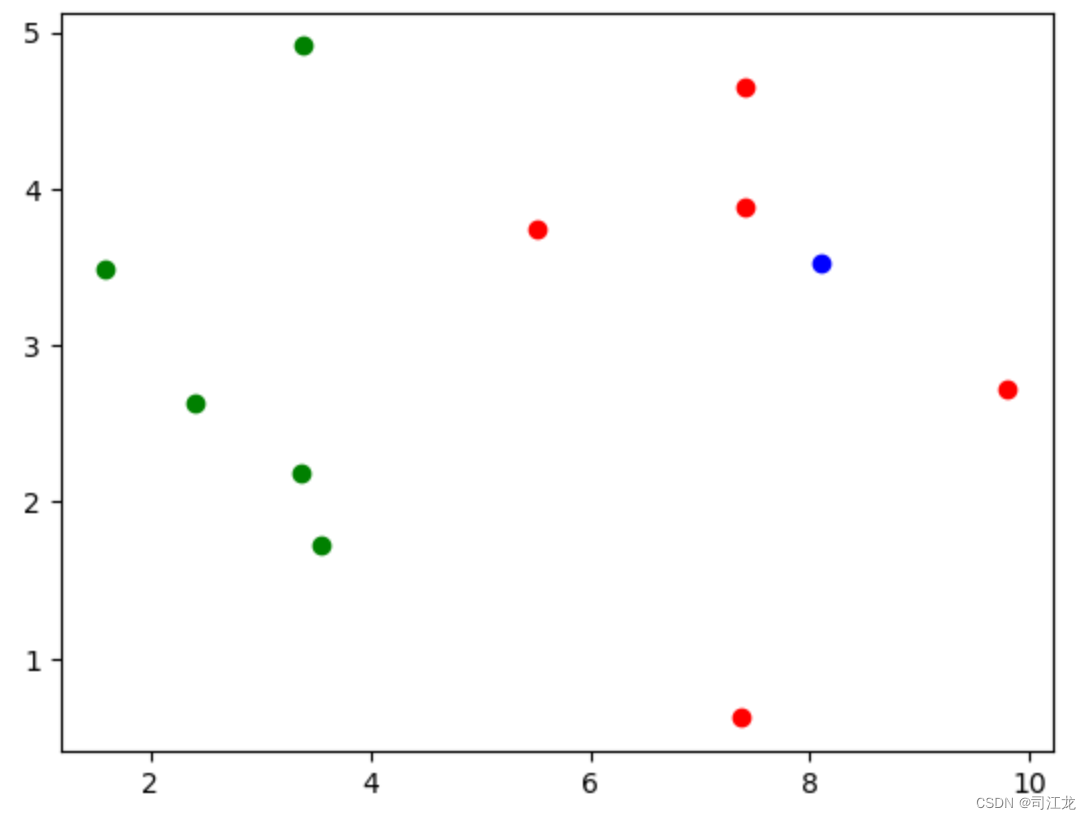

knn实现过程（求蓝色点属于哪一类特征）

from math import sqrt
from collections import Counter
#### 第一步 计算 x 新的 点 和 矩阵里每个点的 欧拉距离
### 分步骤解析
distances = [] #新的x数据与所有点的距离容器
for arr in x_train:
    a = (arr - x) # 原始数据 arr[a,b]- 新的数据 x[a,b] 
    b = a**2 # 平方 [x,y]
    c = sqrt(np.sum(b)) # a[x,y] 开方(x + y) = 欧拉距离
    distances.append(c) # 赋值

distances = [sqrt(np.sum((arr - x)** 2)) for arr in x_train] # 简写 同上效果一样
distances

#### 第二步 求 离新的点最近的两个点

nearest = np.argsort(distances)#点的距离又近到远排序拿到索引 = distances 排序（正序） 并 获取 distances 的索引 
k = 6
topk_y = [y_train[i] for i in nearest[:k]] #循环nearest 拿到 y_train对应的类型值 [1, 1, 1, 1, 1, 0]

votes = Counter(topk_y) # Counter({1: 5, 0: 1}) 统计 topk_y 类型的数量（数组元素的数量）
most = votes.most_common(1) #找到票数最多的 1 个元素  [(1, 5)] 类型 1 为 5 次
most[0][0] #取出邻近最终类型  1 红色特征

3、自行封装kNN邻近算法并测试

使用pycharm编辑器创建conda解释器kNN_function包，封装kNN_classify方法

mport numpy as np
from math import sqrt
from collections import Counter


def kNN_classify(k,X_train,y_train,x):
    assert 1 <= k <= X_train.shape[0], \
        "the size if X_train must equal to the size of y_train"
    assert X_train.shape[1] == x.shape[0], \
        "the feature number if x nust be equal to X_train"
    distances = [sqrt(np.sum((x_train - x)**2)) for x_train in X_train]
    nearest = np.argsort(distances)
    topK_y = [y_train[i] for i in nearest[:k]]
    votes = Counter(topK_y)

    return votes.most_common(1)[0][0]

以下是jupyter NotBook 新建的测试kNN方法的代码，注意测试的py文件需要和kNN_function包在

同一目录下

import numpy as np
import matplotlib.pyplot as plt
raw_data_x = [[3.37086107,2.18526045],
             [3.55642876,1.72918867],
             [1.58794548,3.49198377],
             [3.38792636,4.91105222],
             [2.40416776,2.63642478],
             [7.40395068,4.65064059],
             [5.52275251,3.73818019],
             [9.79558531,2.72280788],
             [7.41003511,3.88750517],
             [7.3726532,0.62106226]]
raw_data_y = [0,0,0,0,0,1,1,1,1,1]
X_train = np.array(raw_data_x)
y_train = np.array(raw_data_y)
x = np.array([8.09565541,3.52106226])
%run kNN_function/kNN.py #加载kNN.py文件
predict_y = kNN_classify(6,X_train,y_train,x)
predict_y

4、使用scikit-learn中的kNN

from sklearn.neighbors import KNeighborsClassifier #引用scikit-learn中的 KNeighborsClassifier 类
knnClassfierObj = KNeighborsClassifier(n_neighbors=6)
knnClassfierObj.fit(X_train,y_train)
x_predict = x.reshape(1,-1) #一维转矩阵
y_predict = knnClassfierObj.predict(x_predict)# 传入新的数据
y_predict[0]

 5、仿照scikit-learn封装kNN

import numpy as np
from math import sqrt
from collections import Counter
from .metrics import accuracy_score

class KNNClassifier:

    def __init__(self, k):
        """初始化kNN分类器"""
        assert k >= 1, "k must be valid"
        self.k = k
        self._X_train = None
        self._y_train = None

    def fit(self, X_train, y_train):
        """根据训练数据集X_train和y_train训练kNN分类器"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"
        assert self.k <= X_train.shape[0], \
            "the size of X_train must be at least k."

        self._X_train = X_train
        self._y_train = y_train
        return self

    def predict(self, X_predict):
        """给定待预测数据集X_predict，返回表示X_predict的结果向量"""
        assert self._X_train is not None and self._y_train is not None, \
                "must fit before predict!"
        assert X_predict.shape[1] == self._X_train.shape[1], \
                "the feature number of X_predict must be equal to X_train"

        y_predict = [self._predict(x) for x in X_predict]
        return np.array(y_predict)

    def _predict(self, x):
        """给定单个待预测数据x，返回x的预测结果值"""
        assert x.shape[0] == self._X_train.shape[1], \
            "the feature number of x must be equal to X_train"

        distances = [sqrt(np.sum((x_train - x) ** 2))
                     for x_train in self._X_train]
        nearest = np.argsort(distances)

        topK_y = [self._y_train[i] for i in nearest[:self.k]]
        votes = Counter(topK_y)

        return votes.most_common(1)[0][0]

    def score(self, X_test, y_test):
        """根据测试数据集 X_test 和 y_test 确定当前模型的准确度"""

        y_predict = self.predict(X_test)
        return accuracy_score(y_test, y_predict)

    def __repr__(self):
        return "KNN(k=%d)" % self.k

6、使用sklearn数据集测试封装的算法

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

iris = datasets.load_iris() # 获取 sklearn  datasets 的 莺尾花测试数据集
X = iris.data # (150,4) 矩阵
y = iris.target # （150,）数组
# train_test_split 拆分数据集 1 训练数据集  2 测试数据集
shuffle_indexes = np.random.permutation(len(X)) # 拿到 X 数据集 随机的 索引
test_ratio = 0.2 #训练数据集和测试数据集分配比例
test_size = int(len(X) * test_ratio)
test_indexes = shuffle_indexes[:test_size] #测试数据集索引
train_indexes = shuffle_indexes[test_size:]#训练数据集索引

#训练数据集
x_train = X[train_indexes]
y_train = y[train_indexes]

#测试数据集
x_test = X[test_indexes]
y_test = y[test_indexes]

from playML.kNN import KNNClassifier

my_knn_clf = KNNClassifier(k=3)
my_knn_clf.fit(x_train, y_train)
y_predict = my_knn_clf.predict(x_test)
print(y_predict)
similarity = sum(y_predict == y_test) / len(y_test)#训练出的数据与测试数据集相似度

#使用sklearn.model_selection 类库生成 训练和测试数据集
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
print(len(X_train))
print(len(X_test))

7、输出结果分类的准确度

当我们有了准确的训练数据集和测试数据集，那么我们怎么验证自己写的算法输出的结果是否标准呢，就用到了结果分类的准确度，通过准确度验证结果和测试数据的相似程度。

下面是代码实现验证过程

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

digits = datasets.load_digits()# 加载 sklearn datasets 下的 digits 数据集

X = digits.data #原始数据集

y = digits.target #数据特征分类 target

#可视化查看一下数据的特性
import matplotlib
import matplotlib.pyplot as plt
some_digit = X[666]
some_digit_image = some_digit.reshape(8, 8)
plt.imshow(some_digit_image, cmap = matplotlib.cm.binary)
plt.show()

#切割原始数据集，获取 训练数据和测试数据
from playML.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_ratio=0.2)

#加载 KNNClassifier 类库
from playML.kNN import KNNClassifier

my_knn_clf = KNNClassifier(k=3) #init初始化
my_knn_clf.fit(X_train, y_train) #训练数据

y_predict = my_knn_clf.predict(X_test) #训练的结果
sum(y_predict == y_test) / len(y_test) #对比相似度

#使用 封装 metrics 类库 的 accuracy_score方法
from playML.metrics import accuracy_score
accuracy_score(y_test, y_predict)

#使用KNNClassifier类库 score 方法直接获取相似度
my_knn_clf.score(X_test, y_test)

#使用sklearn.metrics 获取分类准确度
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=666)

from sklearn.neighbors import KNeighborsClassifier

knn_clf = KNeighborsClassifier(n_neighbors=3)
knn_clf.fit(X_train, y_train)
y_predict = knn_clf.predict(X_test)

from sklearn.metrics import accuracy_score

accuracy_score(y_test, y_predict)
knn_clf.score(X_test, y_test)

 封装 metrics 类库 准确度 accuracy_score 方法

import numpy as np


def accuracy_score(y_true, y_predict):
    '''计算y_true和y_predict之间的准确率'''
    assert y_true.shape[0] == y_predict.shape[0], \
        "the size of y_true must be equal to the size of y_predict"

    return sum(y_true == y_predict) / len(y_true)

8、超参数和模型参数

超参数：在算法运行前需要决定的参数

模型参数：算法过程中学习的参数

算法工程师平常的调参就是调整的超参数，kNN算法没有模型参数，kNN算法中的k是典型的超参数

问题：怎么调整超参数，怎么获得最优的超参数

下面是代码实现

import numpy as np
from sklearn import datasets

digits = datasets.load_digits()
X = digits.data
y = digits.target
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=666)

from sklearn.neighbors import KNeighborsClassifier

#寻找最好的k
best_score = 0.0 #基础相似度
best_k = -1 #基础k
#循环k 取相似度最优的 k 
for k in range(1, 11):
    knn_clf = KNeighborsClassifier(n_neighbors=k)
    knn_clf.fit(X_train, y_train)
    score = knn_clf.score(X_test, y_test)
    if score > best_score:
        best_k = k
        best_score = score
        
print("best_k =", best_k)
print("best_score =", best_score)

在kNN邻近算法还存在要不要考虑 新的节点和多类型节点的距离权重，例如下面例子，虽然蓝色节点的数量多，但是节点离红色更近，如果考虑节点与特征的距离，那么属于蓝色特征就是错误的。

还有如果不考虑节点的距离，假如k值是3，获得的节点特征是平票的话，那么这个节点应该属于哪一类特征，之前的算法就满足不了。 假如距离就可以很好的解决平票的问题。

在klearn.neighbors.KNeighborsClassifier 还有一个超参数（weights）就是控制算法考虑不考虑节点距离的，下面是实例代码

best_score = 0.0
best_k = -1
best_method = ""
for method in ["uniform", "distance"]: # distance 考虑节点距离  uniform 不考虑
    for k in range(1, 11):
        knn_clf = KNeighborsClassifier(n_neighbors=k, weights=method)
        knn_clf.fit(X_train, y_train)
        score = knn_clf.score(X_test, y_test)
        if score > best_score:
            best_k = k
            best_score = score
            best_method = method
        
print("best_method =", best_method)
print("best_k =", best_k)
print("best_score =", best_score)

在空间中节点距离不只是有欧拉距离，还有曼哈顿距离、明可夫斯距离，下面是三个距离的数学公式明可夫斯距离的p就是klearn.neighbors.KNeighborsClassifier里另外一个超参数p

下面是代码示例

best_score = 0.0
best_k = -1
best_p = -1

for k in range(1, 11):
    for p in range(1, 6):
        knn_clf = KNeighborsClassifier(n_neighbors=k, weights="distance", p=p)
        knn_clf.fit(X_train, y_train)
        score = knn_clf.score(X_test, y_test)
        if score > best_score:
            best_k = k
            best_p = p
            best_score = score
        
print("best_k =", best_k)
print("best_p =", best_p)
print("best_score =", best_score)

9、网格搜索与kNN算法中更多的超参数

import numpy as np
from sklearn import datasets

digits = datasets.load_digits()
X = digits.data
y = digits.target

# 获取训练和测试数据集
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=666)

from sklearn.neighbors import KNeighborsClassifier
#grid Search 搜索配置参数
param_grid = [
    {
        'weights': ['uniform'], 
        'n_neighbors': [i for i in range(1, 11)]
    },
    {
        'weights': ['distance'],
        'n_neighbors': [i for i in range(1, 11)], 
        'p': [i for i in range(1, 6)]
    }
]

knn_clf = KNeighborsClassifier()

from sklearn.model_selection import GridSearchCV

#GridSearchCV参数  knn_clf 默认的KNeighborsClassifier对象 param_grid 配置参数  n_jobs cpu核数 -1 最优配置 默认值为 1  verbose 是否输出运行信息
grid_search = GridSearchCV(knn_clf, param_grid,n_jobs=-1,verbose=2)

%%time
res = grid_search.fit(X_train, y_train)
print(res)
print(grid_search.best_estimator_)  #最佳分类器
print(grid_search.best_score_) #最佳分类器的相似度
print(grid_search.best_params_) #最佳超参数

10、数据归一化 Featuer Scaling

最值归一化

最值归一化（Min-Max Normalization），也称为区间缩放法，是一种常用的数据归一化方法。它的主要思想是将数据的取值范围缩放到一个预定的区间，通常是 [0, 1]。这种归一化方法可以使不同特征的数据具有相同的尺度，有助于提高模型的性能，特别是对于那些依赖于距离度量的算法，如 k-最近邻算法（k-NN）或支持向量机（SVM）等。

最值归一化的公式如下：

import numpy as np
import matplotlib.pyplot as plt
x = np.random.randint(0, 100, 100) 
x = (x - np.min(x)) / (np.max(x) - np.min(x))

均值方差归一化

均值方差归一化，又称为Z-score标准化（Z-score Normalization），是一种常用的数据归一化方法。这种方法通过对原始数据进行线性变换，使其变成均值为0，标准差为1的标准正态分布。均值方差归一化的过程如下：

X2 = np.random.randint(0, 100, (50, 2))
X2 = np.array(X2, dtype=float)
X2[:,0] = (X2[:,0] - np.mean(X2[:,0])) / np.std(X2[:,0]) #对x2的第0列进行均值方差归一化

最值归一化和均值方差归一化的区别

         最值归一化适用于大多数情况，尤其是在数据分布未知或者存在离群值的情况下，具有较好的鲁棒性，适用于梯度下降等优化算法。

        方差归一化适用于有明显边界的情况，可以将数据缩放到一个预定的范围内，适用于对输入数据范围有明确要求的模型。

使用Scikit-learn中的Scaler对 鸢尾花数据集进行均值方差归一化并训练数据分类准确度demo

import numpy as np
from sklearn import datasets

# 导入必要的库

iris = datasets.load_iris()

# 加载鸢尾花数据集

X = iris.data
y = iris.target

# 提取特征和标签

from sklearn.model_selection import train_test_split
# 导入数据集划分工具

# 分割训练数据和测试数据
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=666)

from sklearn.preprocessing import StandardScaler
# 导入均值方差归一化工具

standardScalar = StandardScaler()
# 创建均值方差归一化的对象

standardScalar.fit(X_train)
# 用训练数据集来拟合均值和标准差

standardScalar.mean_
# 输出训练数据集特征的均值

standardScalar.scale_
# 输出训练数据集特征的标准差

X_train = standardScalar.transform(X_train)
# 使用拟合的均值和标准差来对训练数据进行归一化

X_test_standard = standardScalar.transform(X_test)
# 使用拟合的均值和标准差来对测试数据进行归一化

from sklearn.neighbors import KNeighborsClassifier
# 导入K近邻分类器

knn_clf = KNeighborsClassifier(n_neighbors=3)
# 创建K近邻分类器，设置邻居数为3

knn_clf.fit(X_train, y_train)
# 使用归一化后的训练数据进行模型训练

knn_clf.score(X_test_standard, y_test)
# 使用归一化后的测试数据来评估模型性能并输出准确度

11、k近邻算法总结

K近邻（K-Nearest Neighbors, KNN）算法是一种简单且有效的监督学习算法，适用于分类和回归问题。以下是对KNN算法的总结和补充：

适用于多分类问题：KNN天然适用于解决多分类问题，因为它可以根据邻近的样本进行投票或者取频率最高的类别作为预测结果。

思想简单、效果强大：KNN算法的核心思想是基于样本的特征空间中的距离进行分类或回归预测，其简单直观的思想在实践中表现出了较好的效果。

可用于回归问题：除了分类问题，KNN也可应用于回归任务。在回归问题中，KNN根据邻居样本的平均值或加权平均值来预测目标变量的值，例如学生分数的预测、房价的预测、股市预测等。

效率低下：KNN算法的主要缺点之一是其效率低下，尤其是对于大型数据集。由于KNN需要在预测时计算新样本与所有训练样本之间的距离，因此时间复杂度为O(m*n)，其中m是训练样本数，n是特征数。

维度灾难：在高维度数据中，KNN算法可能会受到“维度灾难”的影响。随着维度的增加，样本之间的距离可能变得无法区分，导致无法有效区分不同类别的样本。因此，在处理高维度数据时，需要谨慎选择K值和特征选择，以避免维度灾难的影响。

总的来说，KNN算法在实践中表现出了简单易用、适用于多种问题的优势，但也需要注意其效率低下和维度灾难的问题。在应用KNN算法时，需要根据具体情况选择合适的参数和预处理方法，以获得更好的性能和效果。

五、线性回归算法

线性回归算法的概念和特点

线性回归是一种经典的统计学算法，旨在建立自变量与因变量之间的线性关系模型。其优化目标是通过最小化预测值与实际观测值之间的残差平方和，来确定最佳拟合直线的斜率和截距。该算法具有以下特点：

1. 解决回归问题： 线性回归广泛用于解决回归分析中的各种问题，如预测房价、销售量等。

2. 思想简单，实现容易： 线性回归的基本思想直观简单，易于理解和实现，是入门机器学习的理想选择。

3. 许多强大的非线性模型的基础： 尽管线性回归本身建模能力有限，但它为许多复杂的非线性模型提供了基础和参考，如多项式回归、岭回归和 Lasso 回归等。

4. 结果具有很好的可解释性： 由于模型直接拟合一条直线，因此其结果具有很强的可解释性，可以清晰地解释自变量与因变量之间的关系。

5. 蕴含机器学习中的很多重要思想： 线性回归涉及到机器学习中的许多重要概念和思想，如损失函数、梯度下降等，对于理解和学习其他机器学习算法具有重要意义。

总的来说，线性回归虽然简单，但在许多实际问题中仍然是一种强大且有用的工具，它为深入理解和探索数据之间的关系提供了重要的起点。

分类问题和回归问题的区别

分类问题主要是解决输入数据是属于模型中的哪一类，而回归问题目标变量是连续的主要用于预测

简单线性回归到多元线性回归

简单线性回归模型表达式：y=ax+b

为了更好的理解简单线性回归和上面的表达式，我们拿房子的面积对应影响房子的价格举例

因变量：x = 房子的面积       自变量：y  = 房子的价格

问题：那么怎么可以通过一个数据集得到一个机器学习的模型，再通过新的房子面积预测出房子的价格呢？

这就是一个简单的线性回归问题。

如上图红色斜线，这条斜线就是最好地拟合数据，也就是模型表达式里的 ax + b。

其中a是斜率，这个好理解，也就是直线的倾斜度。

b是截距，截距就是这条斜线的起始点，那为什么要加入截距呢，因为并不是所有的关系都会经过原点。例如，在一些情况下，当自变量为零时，因变量并不一定为零。通过加入截距，我们允许直线在 y 轴上移动，以更好地拟合数据。

现在，我们将考虑多元线性回归，这时我们有多个自变量x来预测因变量。

假设我们有 n 个自变量 x1​,x2​,…,xn​，以及一个因变量 y。

模型表达式变成：y = a1​*x1 ​+ a2*​x2 ​+…+ an​*xn ​+ b

这里，a1​,a2​,…,an​ 是各个自变量的系数，而 b 是截距。

在多元线性回归中，我们不再考虑一个自变量对因变量的影响，而是考虑多个自变量同时对因变量的影响。每个自变量都有一个相关系数，表示其对因变量的影响程度。

例如，假设我们仍然以房价为例，此时我们考虑房子的面积 x1​、卧室的数量 x2​ 和街区的犯罪率 x3​ 对房价 y 的影响。那么模型就可以表示为：

y=a1​⋅面积+a2​⋅卧室数量+a3​⋅犯罪率+b

在多元线性回归中，我们的目标仍然是通过找到最佳的系数 a1​,a2​,a3​,…,an​ 和截距 b，使得模型最好地拟合数据。我们可以通过最小化平方损失函数来进行训练。

那么最小化误差平方怎么通过损失函数得到a和b的？

可以通过最小二乘法和梯度下降来直接求解线性回归的参数 a 和 b，下面是具体介绍

最小二乘法求解

来直接求解线性回归的参数 a 和 b

当通过最小二乘法来直接求解线性回归的参数 a 和 b 时，我们实际上是在最小化损失函数的过程中得到了解析解。最小二乘法的步骤如下：

1. 计算样本均值： 计算自变量 x 和因变量 y 的均值，分别表示为 ˉxˉ 和 ˉyˉ​。

   

2. 计算斜率 a： 使用最小二乘法的公式计算斜率 a。

   

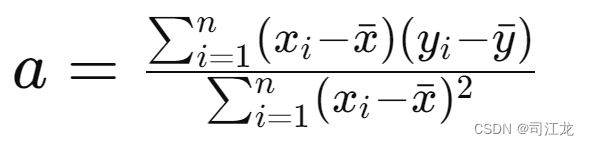
3. 计算截距 b： 利用得到的斜率和均值，计算截距 b。

   

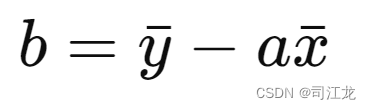
这些步骤直接通过样本数据的计算，而不需要像梯度下降那样进行迭代调整。通过这种方式，我们得到的 a 和 b 就是使得损失函数最小化的最优解。

与梯度下降相比，最小二乘法是一种解析解，可以直接计算出参数的精确值。但需要注意，最小二乘法在某些情况下可能不适用，例如当样本数据量较大或者特征矩阵不满秩时，此时可以使用梯度下降等迭代优化方法。

python 代码实现

import numpy as np

# 输入数据
x = np.array([1., 2., 3., 4., 5.])
y = np.array([1., 3., 2., 3., 5.])

# 计算 x 和 y 的均值
x_mean = np.mean(x)
y_mean = np.mean(y)

# 初始化计算公式中的分子和分母
numerator = 0.0
denominator = 0.0

# 遍历每个数据点，计算分子和分母的累加和
for x_i, y_i in zip(x, y):
    numerator += (x_i - x_mean) * (y_i - y_mean)
    denominator += (x_i - x_mean) ** 2

# 计算斜率 a
a = numerator / denominator

# 计算截距 b
b = y_mean - a * x_mean

# 输出结果
print("斜率 a:", a)
print("截距 b:", b)

梯度下降求解 

梯度下降求解线性回归的参数 a 和 b

最小化误差平方通过损失函数得到 a 和 b 的过程主要涉及优化问题和求解方法。在这里，我们将使用均方误差（Mean Squared Error，MSE）作为损失函数，即：

其中 n 是观测数据的数量，(xi​,yi​) 是数据集中的第 i 个数据点。

最小化误差平方的目标是找到 a 和 b 的值，使得损失函数 L(a,b) 达到最小值。这通常通过梯度下降等优化算法来实现。

梯度下降步骤：

1. 初始化参数 a 和 b： 选择任意初始值作为 a 和 b 的起始点。

2. 计算损失函数的梯度： 计算损失函数对 a 和 b 的偏导数，即梯度。这告诉我们在当前点，损失函数增加最快的方向。

   

3. 更新参数 a 和 b： 使用梯度信息来更新参数，通过学习率（learning rate）乘以梯度的负值，沿着梯度下降的方向更新参数。

   

4. 重复步骤 2 和 3： 重复计算梯度和更新参数的步骤，直到损失函数收敛到最小值或达到预定的迭代次数。

通过这个迭代过程，梯度下降算法调整 a 和 b 的值，使得损失函数逐渐减小，模型的拟合效果逐渐优化。最终得到的 a 和 b 就是能够使模型最优拟合数据的参数。

python 代码实现

import numpy as np

def gradient_descent(x, y, learning_rate=0.01, epochs=1000):
    n = len(x)
    a = 0.0
    b = 0.0

    for epoch in range(epochs):
        # 计算梯度
        a_gradient = -2/n * np.sum(x * (y - (a * x + b)))
        b_gradient = -2/n * np.sum(y - (a * x + b))

        # 更新参数
        a -= learning_rate * a_gradient
        b -= learning_rate * b_gradient

    return a, b

x = np.array([1., 2., 3., 4., 5.])
y = np.array([1., 3., 2., 3., 5.])

a, b = gradient_descent(x, y)

# 打印结果
print("斜率 a:", a)
print("截距 b:", b)

 衡量和评估模型的性能

        针对线性回归模型的预测性能，通常可以使用以下几种指标来进行评估：

1. MAE（Mean Absolute Error） - 平均绝对误差：

   • 计算方法：对于每个预测值和实际值，取它们的绝对值，然后求这些绝对值的平均值。
   • 公式：
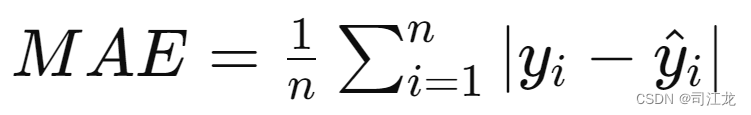
   • MAE对异常值比较敏感，因为它直接考虑每个样本的绝对误差，而不考虑误差的平方。

2. MSE（Mean Squared Error） - 均方误差：

   • 计算方法：对于每个预测值和实际值，取它们的差值的平方，然后求这些平方差的平均值。
   • 公式：
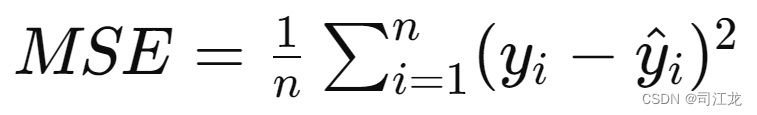
   • MSE对异常值更为敏感，因为它在计算误差时对较大的误差给予更大的权重。

3. RMSE（Root Mean Squared Error） - 均方根误差：

   • 计算方法：是MSE的平方根，通过对MSE取平方根来消除量纲，使得评估指标与原始目标变量的单位一致。
   • 公式：
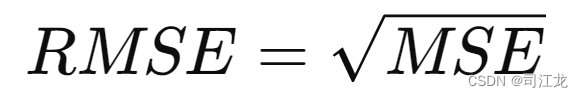
   • RMSE的计算结果与原始目标变量的单位相同，这使得它更容易解释。

MAE、MSE、RMSE的区别

• MAE、MSE和RMSE都是度量模型预测误差的指标，但它们对误差的处理方式不同。
• MAE对每个误差都进行等权重考虑，MSE对较大的误差给予更大的权重，而RMSE在这基础上进行平方根变换，进一步强调了大误差的影响。
• RMSE相比于MAE和MSE更容易受到异常值的影响，因为它在误差的计算中使用了平方，这会放大较大误差的影响。

import numpy as np
from sklearn.metrics import mean_absolute_error, mean_squared_error

# 示例数据
y_true = np.array([1.5, 2.1, 3.8, 4.2, 5.0])
y_pred = np.array([1.2, 2.0, 3.5, 4.0, 4.8])

# 计算MAE
mae = mean_absolute_error(y_true, y_pred)
print(f"MAE: {mae}")

# 计算MSE
mse = mean_squared_error(y_true, y_pred)
print(f"MSE: {mse}")

# 计算RMSE
rmse = np.sqrt(mse)
print(f"RMSE: {rmse}")

R-squared（R平方）是一种常用于评估回归模型性能的指标，也被称为决定系数。它提供了一个衡量模型对目标变量方差解释程度的度量，即模型能够解释目标变量变化的百分比。

它和分类算法的百分比是一样的，取值范围在0到1之间，越接近1越好。

六、梯度下降法

1、什么是梯度下降法

梯度下降法是一种优化算法，常用于机器学习中的参数优化问题，尤其是在训练模型时。其基本思想是通过迭代的方式，沿着梯度的反方向逐步调整参数，从而降低目标函数（损失函数）的值，达到找到最优解的目的。

学习率超参数：的取值太小影响获得最优解的速度，取值太大有可能获取不到最优解

2、梯度下降法的数学公式

梯度下降法是一种优化算法，用于最小化一个函数的值，特别是在机器学习中，它通常用于调整模型参数以最小化损失函数。其数学公式如下：

假设我们有一个待优化的函数 �(�)J(θ)，其中 �θ 是要优化的参数向量。

1. 批量梯度下降（Batch Gradient Descent）： 在每一次迭代中，通过计算整个训练集的梯度来更新参数。

   更新规则： θ=θ−α∇J(θ) 其中，

   • α 是学习率（步长），控制着参数更新的幅度；
   • ∇J(θ) 是损失函数 J(θ) 关于参数向量 θ 的梯度。

2. 随机梯度下降（Stochastic Gradient Descent）： 在每一次迭代中，只使用一个随机样本来估计梯度并更新参数。

   更新规则： θ=θ−α∇J(θ;x(i),y(i)) 其中，

   • (x(i),y(i)) 是随机选择的训练样本；
   • ∇J(θ;x(i),y(i)) 是损失函数关于参数 θ 在样本 (x(i),y(i)) 上的梯度。

3. 小批量梯度下降（Mini-batch Gradient Descent）： 在每一次迭代中，使用一个随机选择的小批量样本来估计梯度并更新参数。

   更新规则： θ=θ−α∇J(θ;Xbatch​,ybatch​) 其中，

   • (Xbatch​,ybatch​) 是随机选择的小批量训练样本；
   • ∇J(θ;Xbatch​,ybatch​) 是损失函数关于参数 θ 在小批量样本(Xbatch​,ybatch​) 上的梯度。

这些是梯度下降法的基本数学公式，通过不断迭代更新参数，梯度下降法能够逐步降低损失函数的值，使模型参数向最优值靠近。

3、python实现梯度下降

import numpy as np
import matplotlib.pyplot as plt

# 生成用于绘图的 x 值
plot_x = np.linspace(-1., 6., 141)
# 计算对应的 y 值，这里使用一个简单的二次函数
plot_y = (plot_x - 2.5) ** 2 - 1.

# 绘制原始曲线图
plt.plot(plot_x, plot_y)
plt.show()

# 设置梯度下降的收敛条件和学习率
epsilon = 1e-8
eta = 0.1

# 定义损失函数 J(theta) 和其导数 dJ(theta)
def J(theta):
    return (theta - 2.5) ** 2 - 1.

def dJ(theta):
    return 2 * (theta - 2.5)

# 初始化参数 theta
theta = 0.0

# 梯度下降过程
while True:
    gradient = dJ(theta)  # 计算梯度
    last_theta = theta  # 保存上一次的参数值
    theta = theta - eta * gradient  # 更新参数

    # 判断是否满足收敛条件
    if abs(J(theta) - J(last_theta)) < epsilon:
        break

# 打印最终的参数值和损失值
print("Final theta:", theta)
print("Final J(theta):", J(theta))

# 可视化梯度下降过程

# 重新初始化参数 theta
theta = 0.0
theta_history = [theta]

# 再次进行梯度下降，记录每一步的参数值
while True:
    gradient = dJ(theta)
    last_theta = theta
    theta = theta - eta * gradient
    theta_history.append(theta)

    # 判断是否满足收敛条件
    if abs(J(theta) - J(last_theta)) < epsilon:
        break

# 绘制损失函数曲线以及梯度下降过程中的参数值
plt.plot(plot_x, J(plot_x))
plt.plot(np.array(theta_history), J(np.array(theta_history)), color="r", marker='+')
plt.show()

注意：在训练实际的数据，需要注意需要把数据进行归一化再训练

4、 Python实现随机梯度下降法

import numpy as np
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import SGDRegressor
from playML.LinearRegression import LinearRegression

# 获取加利福尼亚房价数据集
california_housing = fetch_california_housing()
X = california_housing.data  # 特征矩阵
y = california_housing.target  # 目标变量（房价）
# 使用 sklearn 的 train_test_split 函数划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

# 数据标准化
standardScaler = StandardScaler()
X_train_standard = standardScaler.fit_transform(X_train)
X_test_standard = standardScaler.transform(X_test)

# 使用自己实现的 LinearRegression 进行梯度下降
lin_reg3 = LinearRegression()
%time lin_reg3.fit_gd(X_train_standard, y_train)
a = lin_reg3.score(X_test_standard, y_test)
print(a)
# 使用 sklearn 中的 SGDRegressor 进行梯度下降
sgd_reg = SGDRegressor(max_iter=10, random_state=666)
%time sgd_reg.fit(X_train_standard, y_train)
sgd_reg.score(X_test_standard, y_test)

七、主成分分析法PCA

PCA概念和特点

PCA是一个非监督的机器学习算法，主要用于数据的降维，数据集降维后可以提升数据集的训练速度，对于大的数据集训练速度提升非常有效，而且通过降维，还可以发现更便于人类理解的特征，

其他应用：数据特征可视化，去噪

主成分分析法的数学公式

推导过程看不懂没关系，先理解，这个需要数学功底

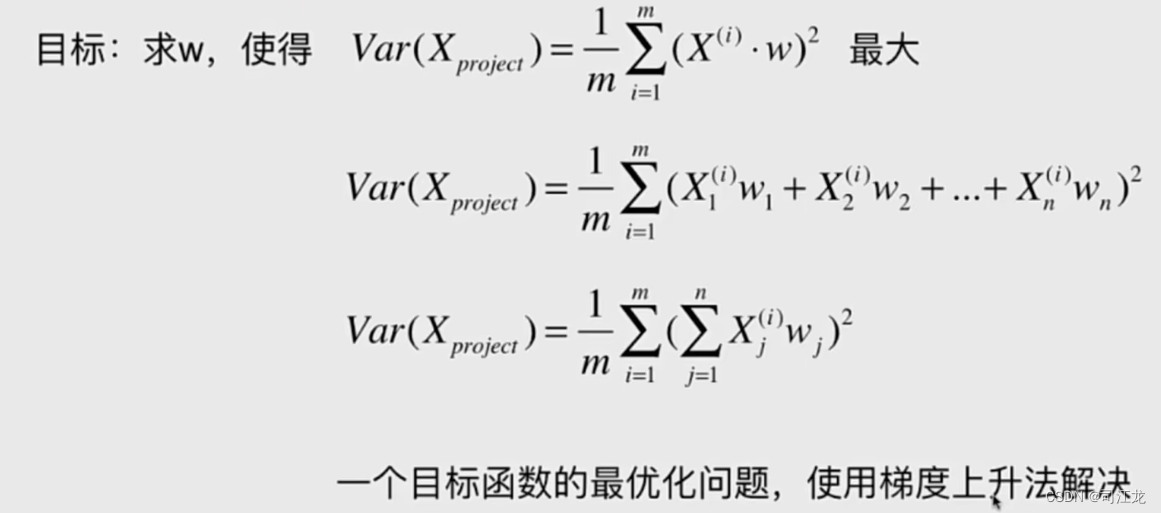
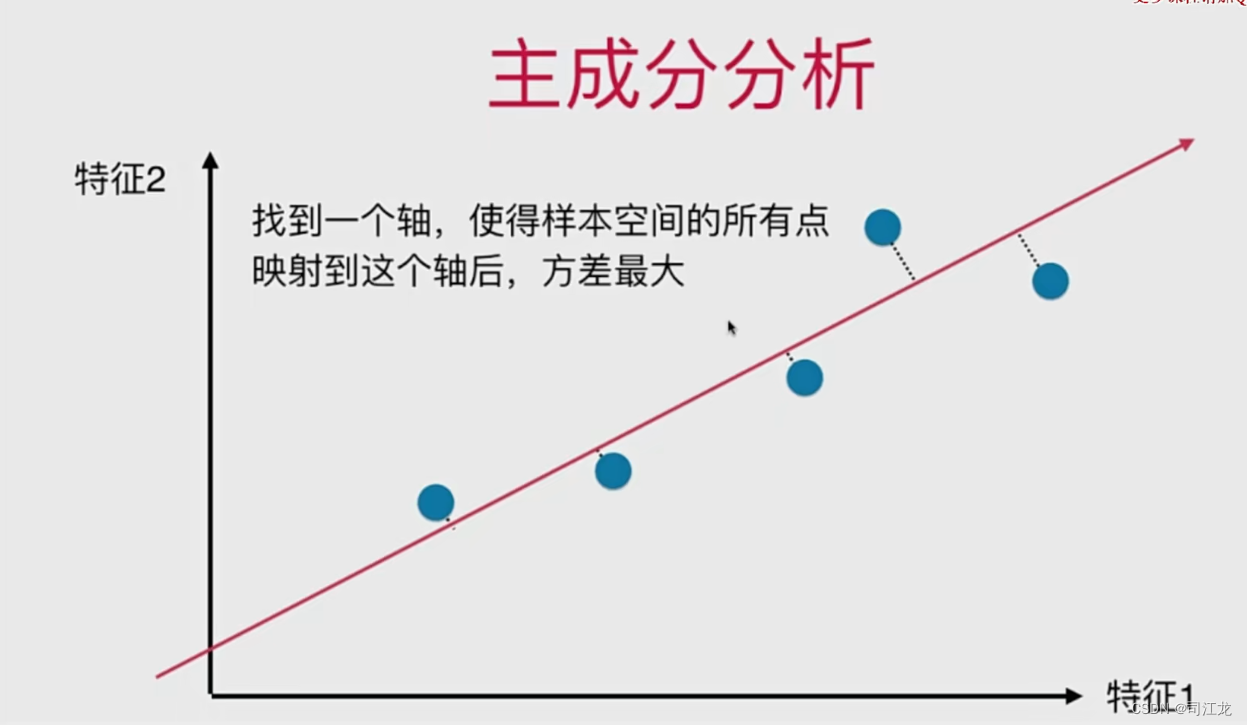
主成分分析和线性回归的区别

主成分分析和线性回归虽然都涉及到线性关系，但它们的目的、应用和结果有着明显的不同。主成分分析旨在理解数据的结构和降低维度，而线性回归旨在建立预测模型并理解自变量与因变量之间的关系。

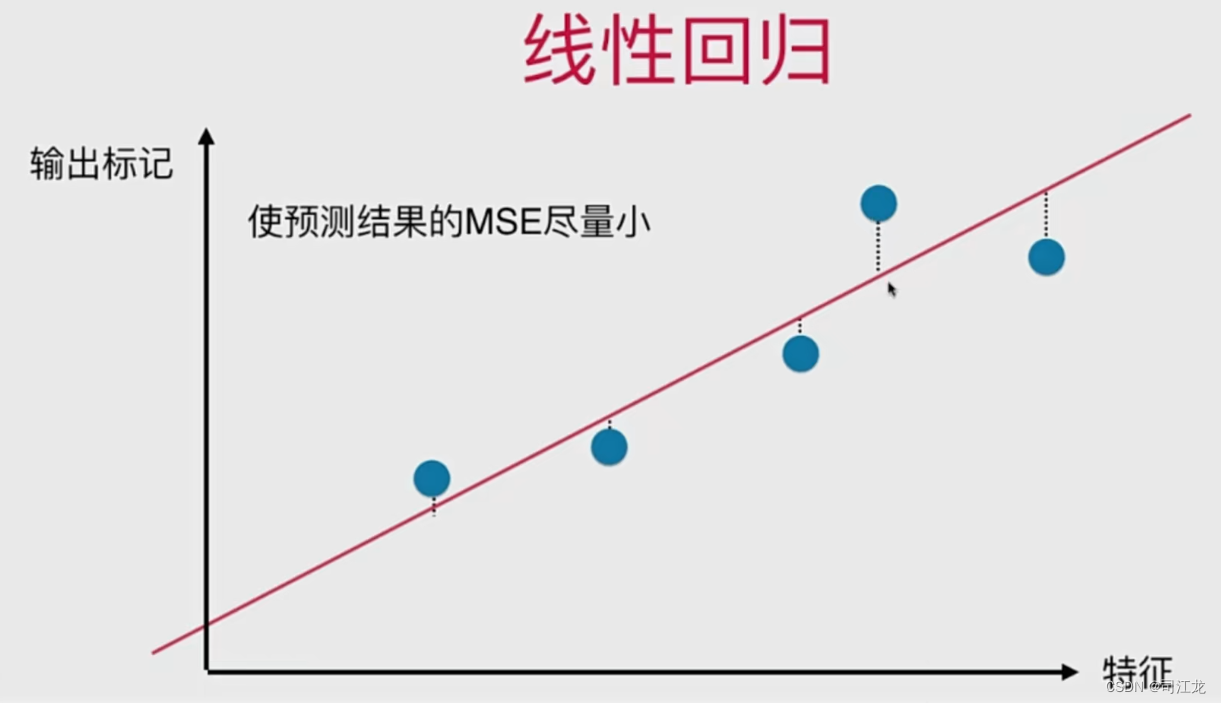
梯度上升法解决PCA问题

公式

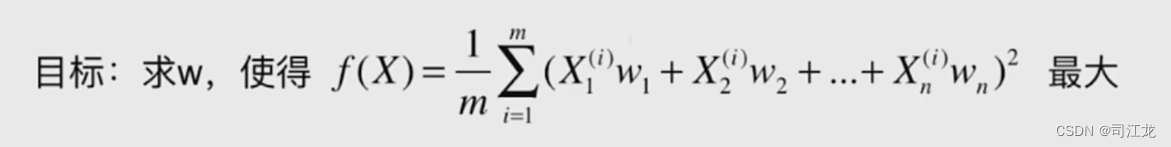
代码实现梯度上升演示过程

import numpy as np
import matplotlib.pyplot as plt

X = np.empty((100, 2))
X[:,0] = np.random.uniform(0., 100., size=100)
X[:,1] = 0.75 * X[:,0] + 3. + np.random.normal(0, 10., size=100)

plt.scatter(X[:,0], X[:,1])
plt.show()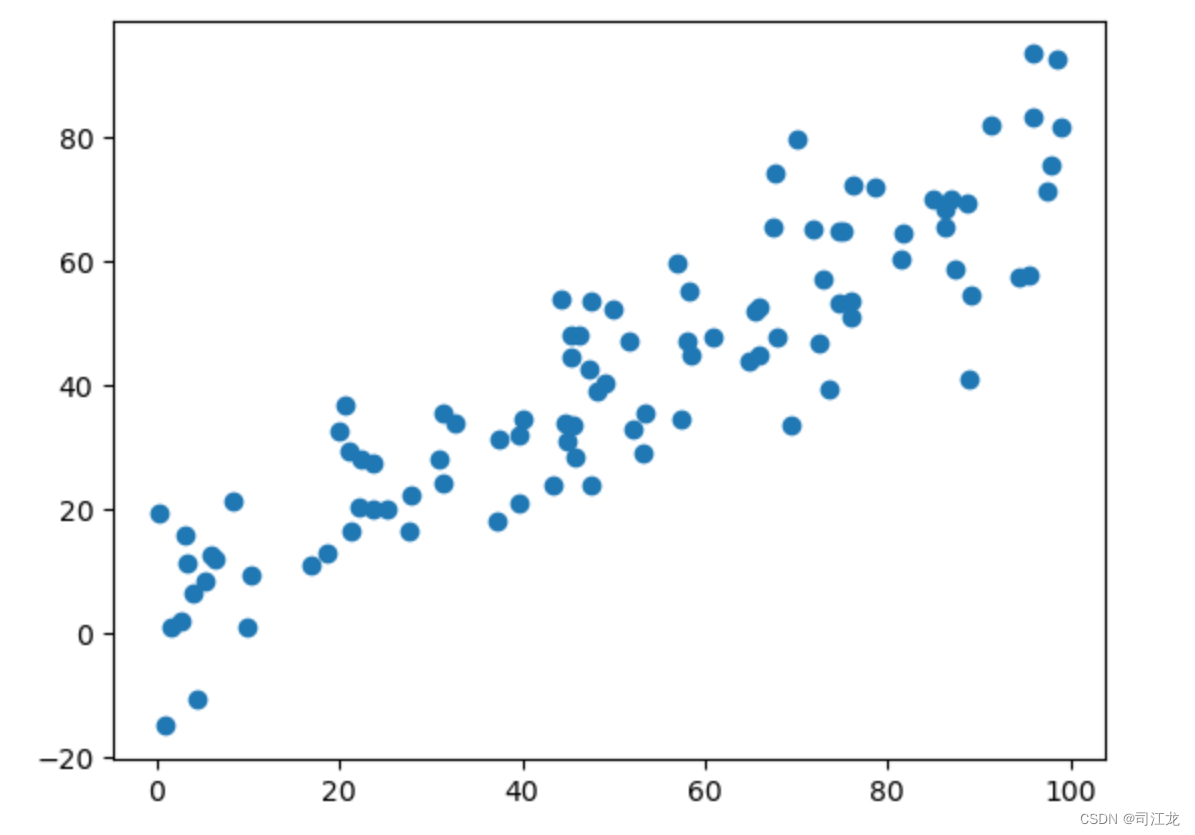

 

# 函数：将数据集的每个特征的均值归零
def demean(X):
    return X - np.mean(X, axis=0)

# 对数据进行均值归零处理
X_demean = demean(X)
# 绘制均值归零后的数据散点图
plt.scatter(X_demean[:,0], X_demean[:,1])
plt.show()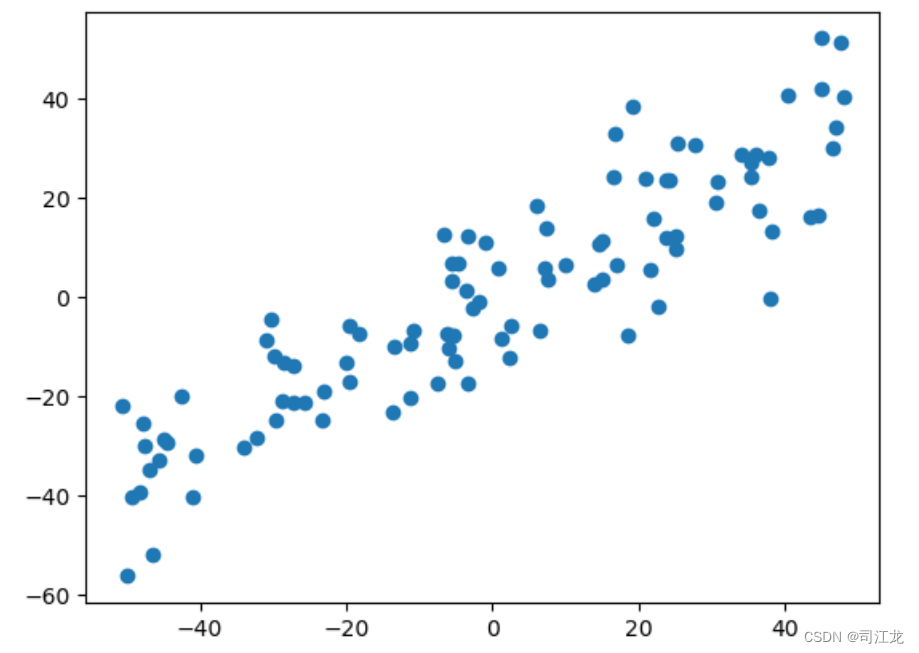

# 函数：定义优化目标函数
def f(w, X):
    return np.sum((X.dot(w)**2)) / len(X)

# 函数：定义优化目标函数的梯度
def df_math(w, X):
    return X.T.dot(X.dot(w)) * 2. / len(X)

# 函数：用于调试，计算目标函数梯度的数值近似
def df_debug(w, X, epsilon=0.0001):
    res = np.empty(len(w))
    for i in range(len(w)):
        w_1 = w.copy()
        w_1[i] += epsilon
        w_2 = w.copy()
        w_2[i] -= epsilon
        res[i] = (f(w_1, X) - f(w_2, X)) / (2 * epsilon)
    return res

# 函数：将向量转化为单位向量
def direction(w):
    return w / np.linalg.norm(w)

# 函数：梯度上升法求解主成分
def gradient_ascent(df, X, initial_w, eta, n_iters = 1e4, epsilon=1e-8):
    w = direction(initial_w) 
    cur_iter = 0

    while cur_iter < n_iters:
        gradient = df(w, X)
        last_w = w
        w = w + eta * gradient
        w = direction(w) # 每次求一个单位方向
        if(abs(f(w, X) - f(last_w, X)) < epsilon):
            break
            
        cur_iter += 1

    return w

# 随机初始化权重向量
initial_w = np.random.random(X.shape[1]) 
eta = 0.001

# 使用优化目标函数的解析梯度进行梯度上升
gradient_ascent(df_math, X_demean, initial_w, eta)

# 使用数值近似梯度进行梯度上升
gradient_ascent(df_debug, X_demean, initial_w, eta)

# 求解主成分并绘制主成分方向
w = gradient_ascent(df_math, X_demean, initial_w, eta)
plt.scatter(X_demean[:,0], X_demean[:,1])
plt.plot([0, w[0]*30], [0, w[1]*30], color='r')
plt.show()

# 使用极端数据集测试
X2 = np.empty((100, 2))
X2[:,0] = np.random.uniform(0., 100., size=100)
X2[:,1] = 0.75 * X2[:,0] + 3.

# 绘制极端数据集散点图
plt.scatter(X2[:,0], X2[:,1])
plt.show()

# 对极端数据进行均值归零处理
X2_demean = demean(X2)
# 求解主成分并绘制主成分方向
w2 = gradient_ascent(df_math, X2_demean, initial_w, eta)
plt.scatter(X2_demean[:,0], X2_demean[:,1])
plt.plot([0, w2[0]*30], [0, w2[1]*30], color='r')
plt.show()

 

以上代码主要是实现了主成分分析（PCA）的一个简单版本，使用了梯度上升法来寻找数据集中的主成分方向。代码的执行流程如下：

生成了一个二维的随机数据集 X，其中第一个特征与第二个特征之间存在线性关系。
使用 demean() 函数对数据集进行均值归零处理，这是 PCA 中的一项预处理步骤。
定义了目标函数 f(w, X) 和其梯度函数 df_math(w, X)，目标函数表示数据点到主成分的投影距离的平方和，梯度函数表示目标函数的梯度。
实现了一个用于调试的梯度计算函数 df_debug(w, X, epsilon)，用数值方法近似梯度，以验证解析梯度的正确性。
实现了一个函数 direction(w)，用于将向量转化为单位向量。
定义了梯度上升法函数 gradient_ascent(df, X, initial_w, eta, n_iters, epsilon)，其中 df 参数为梯度函数，initial_w 是初始权重向量，eta 是学习率，n_iters 是迭代次数限制，epsilon 是停止迭代的阈值。
使用随机初始化的权重向量调用梯度上升函数，寻找数据集中的主成分方向。
绘制了均值归零后的数据散点图，并在图中绘制了找到的主成分方向。
使用一个极端数据集 X2 进行了相同的处理和绘图，以测试算法对于不同数据集的适用性。 

scikit-learn中的PCA

二维数据简单示例

这段代码生成了一个二维随机数据集 X，其中第一列数据服从均匀分布在0到100之间，第二列数据是第一列数据的0.75倍加上一个常数3再加上一些服从正态分布的噪声。然后使用 PCA 进行降维，设定主成分数量为1，将原始数据集降至一维，并使用 inverse_transform 方法将降维后的数据集恢复至原始维度。最后绘制了原始数据集和降维后再恢复的数据集的散点图，用蓝色表示原始数据，红色表示恢复后的数据。 

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA

# 创建一个二维随机数据集
X = np.empty((100, 2))

# 第一列数据服从均匀分布在0到100之间
X[:,0] = np.random.uniform(0., 100., size=100)

# 第二列数据是第一列数据的0.75倍加上一个常数3再加上一些服从正态分布的噪声
X[:,1] = 0.75 * X[:,0] + 3. + np.random.normal(0, 10., size=100)

# 使用PCA进行降维，设定主成分数量为1
pca = PCA(n_components=1)
pca.fit(X)

# 获取主成分方向
pca.components_

# 将原始数据集降至一维
X_reduction = pca.transform(X)

# 将降维后的数据集恢复至原始维度
X_restore = pca.inverse_transform(X_reduction)

# 绘制原始数据集与降维后再恢复的数据集
plt.scatter(X[:,0], X[:,1], color='b', alpha=0.5, label='Original Data')
plt.scatter(X_restore[:,0], X_restore[:,1], color='r', alpha=0.5, label='Restored Data')
plt.legend()
plt.show()

 多维数据示例

1. 加载手写数字数据集，并将数据集划分为训练集和测试集。
2. 使用原始数据训练KNN分类器，并计算在测试集上的准确率。
3. 使用PCA进行降维，选择保留95%的信息，并对训练集和测试集进行降维处理。
4. 使用降维后的数据训练KNN分类器，并计算在测试集上的准确率。
5. 可视化手写数字数据集在二维空间中的分布，每个数字用不同颜色表示。

from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

# 加载手写数字数据集
digits = datasets.load_digits()
X = digits.data
y = digits.target

# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

# 查看训练集的形状
X_train.shape  

# 初始化KNN分类器
knn_clf = KNeighborsClassifier()

# 训练KNN分类器并计算在测试集上的准确率
knn_clf.fit(X_train, y_train)
knn_clf.score(X_test, y_test)
#精度：0.9

# 使用PCA进行降维，设定主成分数量为2
pca = PCA(n_components=2)
pca.fit(X_train)

# 对训练集和测试集进行降维处理
X_train_reduction = pca.transform(X_train)
X_test_reduction = pca.transform(X_test)

# 使用降维后的数据训练KNN分类器并计算在测试集上的准确率
knn_clf.score(X_test, y_test)
#精度：0.6

#问题：64维数据降为2维后再使用了PCA降维后训练的数据，虽然算法的运行速度提高了，但是识别精度太低了，达不到要求，可以增加一些维度，但是我们具体应该降到多少维呢？

# 查看PCA降维后的解释方差比
pca.explained_variance_ratio_

# 查看PCA降维后的特征解释方差
pca.explained_variance_

# 绘制不同主成分数量下的解释方差比累计曲线
pca = PCA(n_components=X_train.shape[1])
pca.fit(X_train)
plt.plot([i for i in range(X_train.shape[1])], 
         [np.sum(pca.explained_variance_ratio_[:i+1]) for i in range(X_train.shape[1])])
plt.show()
#曲线转为横线的那个点就是我们要取的那个值

scikit-learn中的PCA方法已经实现了自动计算维数功能，我们只需传入需要的精度即可 

# 根据解释方差比选择保留95%的信息
pca = PCA(0.95)
pca.fit(X_train)

# 查看保留95%信息时的主成分数量
pca.n_components_

# 对训练集和测试集进行降维处理
X_train_reduction = pca.transform(X_train)
X_test_reduction = pca.transform(X_test)

# 使用降维后的数据训练KNN分类器并计算在测试集上的准确率
knn_clf.fit(X_train_reduction, y_train)
knn_clf.score(X_test_reduction, y_test)
#0.9

 由于多维是很难可视化的，所以pca将数据降到2维常用于数据特征的可视化

# 可视化手写数字数据集在二维空间中的分布
pca = PCA(n_components=2)
pca.fit(X)
X_reduction = pca.transform(X)
for i in range(10):
    plt.scatter(X_reduction[y==i,0], X_reduction[y==i,1], alpha=0.8)
plt.show()

使用PCA对数据特征进行降噪处理实践过程

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.decomposition import PCA

# 加载手写数字数据集
digits = datasets.load_digits()
X = digits.data  # 特征数据
y = digits.target  # 目标数据

# 为手写数字数据添加噪声
noisy_digits = X + np.random.normal(0, 4, size=X.shape)

# 从添加噪声的数据中选择每个数字的前10个示例
example_digits = noisy_digits[y==0,:][:10]
for num in range(1, 10):
    example_digits = np.vstack([example_digits, noisy_digits[y==num,:][:10]])

# 打印示例数据的形状
print(example_digits.shape)

# 定义一个函数来绘制数字图像
def plot_digits(data):
    # 创建一个10x10的子图
    fig, axes = plt.subplots(10, 10, figsize=(10, 10),
                             subplot_kw={'xticks':[], 'yticks':[]},
                             gridspec_kw=dict(hspace=0.1, wspace=0.1)) 
    # 在每个子图上绘制数字
    for i, ax in enumerate(axes.flat):
        ax.imshow(data[i].reshape(8, 8),
                  cmap='binary', interpolation='nearest',
                  clim=(0, 16))

    # 显示图像
    plt.show()

# 绘制示例数据
plot_digits(example_digits)

# 使用PCA进行降维，保留50%的方差
pca = PCA(0.5).fit(noisy_digits)

# 输出降维后的特征数
print(pca.n_components_)

# 将示例数据转换到PCA空间中
components = pca.transform(example_digits)

# 从PCA空间中重构数据
filtered_digits = pca.inverse_transform(components)

# 绘制重构后的数据
plot_digits(filtered_digits)

 

加载手写数字数据集，并对数据进行处理，然后使用PCA进行降维，最后可视化降维前后的数据，可以很明显的对比降维前后的可视化效果。 

对人脸识别数据集进行PCA 降维

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_lfw_people

# 加载LFW（Labeled Faces in the Wild）人脸数据集
faces = fetch_lfw_people()

# 打印人脸数据的形状
print(faces.data.shape)  # (13233, 2914) 表示共有13233张人脸，每张人脸有2914个特征

# 打印人脸图像的形状
print(faces.images.shape)  # (13233, 62, 47) 表示共有13233张人脸，每张人脸图像的尺寸为62x47像素

# 生成随机索引以重新排列人脸数据
random_indexes = np.random.permutation(len(faces.data))

# 使用随机索引重新排列人脸数据
X = faces.data[random_indexes]

# 选择前36张人脸作为示例
example_faces = X[:36, :]

# 打印示例人脸数据的形状
print(example_faces.shape)

# 定义一个函数来绘制人脸图像
def plot_faces(faces):
    # 创建一个6x6的子图
    fig, axes = plt.subplots(6, 6, figsize=(10, 10),
                             subplot_kw={'xticks':[], 'yticks':[]},
                             gridspec_kw=dict(hspace=0.1, wspace=0.1)) 
    # 在每个子图上绘制人脸图像
    for i, ax in enumerate(axes.flat):
        ax.imshow(faces[i].reshape(62, 47), cmap='bone')  # 由于每张人脸图像尺寸为62x47像素，需要使用reshape函数重新调整形状
    # 显示图像
    plt.show()

# 绘制示例人脸图像
plot_faces(example_faces)

%%time
from sklearn.decomposition import PCA

# 导入PCA模块
pca = PCA(svd_solver='randomized')

# 对人脸数据进行PCA降维
pca.fit(X)

# 打印PCA的主成分（特征向量）的形状
print(pca.components_.shape)

# 绘制PCA的主成分，这些主成分代表了人脸数据的主要特征
plot_faces(pca.components_[:36,:])

# 重新加载LFW人脸数据集，但这次只选择每个人至少有60张人脸图像的人脸数据
faces2 = fetch_lfw_people(min_faces_per_person=60)

# 打印新的人脸数据集的数据形状
print(faces2.data.shape)

# 打印新的人脸数据集的目标名称
print(faces2.target_names)

# 打印新的人脸数据集的目标类别数
print(len(faces2.target_names))

PCA降维和真实人脸图片对比 

 

八、多项式回归和模型泛化

多项式回归和线性回归的对比

线性回归和多项式线性回归都是回归算法，用于建立输入特征与输出目标之间的关系模型。它们之间的主要区别在于模型的形式和复杂度。

import numpy as np 
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

# 生成一组随机的输入特征和对应的输出目标，符合二次多项式关系，并添加高斯噪声
x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100)

# 使用 PolynomialFeatures 对输入特征进行二次多项式转换
poly = PolynomialFeatures(degree=2)
poly.fit(X)
X2 = poly.transform(X)

# 创建线性回归模型并拟合数据
lin_reg2 = LinearRegression()
lin_reg2.fit(X2, y)
y_predict2 = lin_reg2.predict(X2)

# 绘制原始数据散点图和模型拟合的曲线
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r')
plt.show()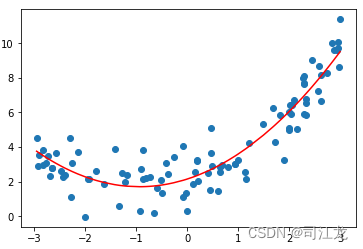

 

过拟合和欠拟合

如何使用线性回归和多项式回归拟合数据，并使用均方误差（MSE）对模型性能进行评估。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.metrics import mean_squared_error

# 生成随机数据
np.random.seed(666)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100)

# 绘制数据散点图
plt.scatter(x, y)
plt.show()

# 使用线性回归拟合数据
lin_reg = LinearRegression()
lin_reg.fit(X, y)
score = lin_reg.score(X, y)
print("Linear Regression R^2 Score:", score)
y_predict = lin_reg.predict(X)
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict[np.argsort(x)], color='r')
plt.show()

# 计算线性回归模型的均方误差
mse_linear = mean_squared_error(y, y_predict)
print("Linear Regression MSE:", mse_linear)

# 定义多项式回归函数
def PolynomialRegression(degree):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lin_reg", LinearRegression())
    ])

# 使用不同次数的多项式回归拟合数据
degrees = [2, 10, 100]
for degree in degrees:
    poly_reg = PolynomialRegression(degree=degree)
    poly_reg.fit(X, y)
    y_predict = poly_reg.predict(X)
    plt.scatter(x, y)
    plt.plot(np.sort(x), y_predict[np.argsort(x)], color='r')
    plt.title(f"Polynomial Regression (Degree = {degree})")
    plt.show()
    mse_poly = mean_squared_error(y, y_predict)
    print(f"Polynomial Regression (Degree = {degree}) MSE:", mse_poly)

# 划分训练集和测试集，并对线性回归和多项式回归模型进行训练和测试
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
models = {"Linear Regression": lin_reg, 
          "Polynomial Regression (Degree=2)": PolynomialRegression(degree=2), 
          "Polynomial Regression (Degree=10)": PolynomialRegression(degree=10), 
          "Polynomial Regression (Degree=100)": PolynomialRegression(degree=100)}

for name, model in models.items():
    model.fit(X_train, y_train)
    y_predict = model.predict(X_test)
    mse_test = mean_squared_error(y_test, y_predict)
    print(f"{name} MSE on Test Set:", mse_test)

 模型的泛化和学习曲线

模型的泛化能力是指模型对未见过的新数据的适应能力。一个具有良好泛化能力的模型能够在训练集之外的数据上表现良好，即使在面对与训练数据不同但属于相同数据分布的新数据时也能够做出准确的预测。模型的泛化能力是衡量模型质量的重要指标之一。

过拟合通常会降低模型的泛化能力。因为过拟合意味着模型在训练集上表现很好，但在测试集或新数据上表现不佳，即模型过度拟合了训练数据中的噪声或随机变化，从而导致了泛化能力的下降。

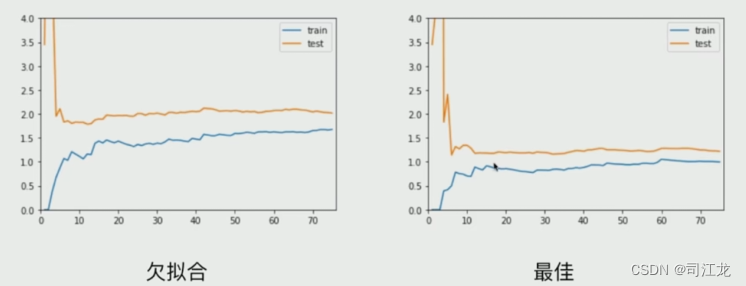
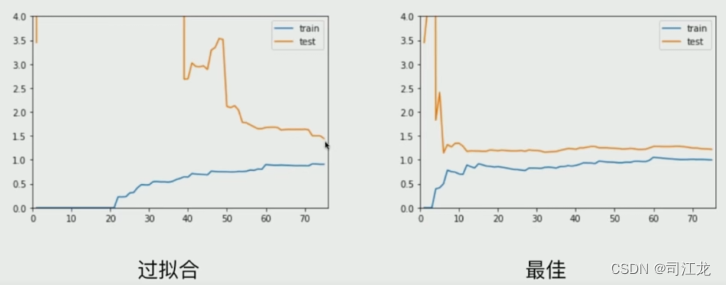
验证数据集与交叉验证 

 

import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import cross_val_score

# 加载手写数字数据集
digits = datasets.load_digits()
X = digits.data  # 特征数据
y = digits.target  # 目标标签

# 划分训练集和测试集，测试集占比为40%
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=666)

# 使用循环遍历不同的 k 和 p 参数组合，寻找最佳的参数
best_k, best_p, best_score = 0, 0, 0
for k in range(2, 11):  # 遍历 k 的取值范围
    for p in range(1, 6):  # 遍历 p 的取值范围
        # 创建 K 近邻分类器，并设置参数
        knn_clf = KNeighborsClassifier(weights="distance", n_neighbors=k, p=p)
        # 在训练集上拟合模型
        knn_clf.fit(X_train, y_train)
        # 在测试集上评估模型得分
        score = knn_clf.score(X_test, y_test)
        # 如果当前模型得分高于历史最佳得分，则更新最佳参数和最佳得分
        if score > best_score:
            best_k, best_p, best_score = k, p, score

# 打印出最佳参数和最佳得分
print("Best K =", best_k)
print("Best P =", best_p)
print("Best Score =", best_score)

# 使用交叉验证寻找最佳参数
best_k, best_p, best_score = 0, 0, 0
for k in range(2, 11):  # 遍历 k 的取值范围
    for p in range(1, 6):  # 遍历 p 的取值范围
        # 创建 K 近邻分类器，并设置参数
        knn_clf = KNeighborsClassifier(weights="distance", n_neighbors=k, p=p)
        # 对模型进行交叉验证，返回每次验证的得分数组
        scores = cross_val_score(knn_clf, X_train, y_train)
        # 计算平均得分
        score = np.mean(scores)
        # 如果当前模型平均得分高于历史最佳得分，则更新最佳参数和最佳得分
        if score > best_score:
            best_k, best_p, best_score = k, p, score

# 打印出最佳参数和最佳得分
print("Best K =", best_k)
print("Best P =", best_p)
print("Best Score =", best_score)

# 使用最佳参数创建 K 近邻分类器，并在测试集上评估模型得分
best_knn_clf = KNeighborsClassifier(weights="distance", n_neighbors=2, p=2)  # 使用上一步得到的最佳参数
best_knn_clf.fit(X_train, y_train)
score = best_knn_clf.score(X_test, y_test)
print("Best KNN Classifier Score on Test Set:", score)

首先加载了手写数字数据集，然后通过 train_test_split 函数将数据集划分为训练集和测试集。接着，使用循环遍历不同的 k 和 p 参数组合，分别在测试集上进行评估，以寻找最佳的参数组合。之后，使用交叉验证寻找最佳参数，通过计算交叉验证的平均得分来评估模型。最后，使用最佳参数创建 K 近邻分类器，并在测试集上评估模型的性能得分。 

偏差和方差

 

可以通过岭回归和LASSO这两种正则化解决模型的过拟合问题 

九、逻辑回归算法 

逻辑回归概念和特点

 逻辑回归（Logistic Regression）是一种用于解决分类问题的机器学习算法，尽管它的名字中包含“回归”一词，但实际上它是一种分类算法，通常用于二分类问题（将样本划分为两个类别）。

特点：简单且高效、输出概率（逻辑回归模型输出的是样本属于某个类别的概率）、线性模型、对数几率函数、可解释性强。

代码实现逻辑回归

LogisticRegression 类实现了逻辑回归模型。它的 fit 方法使用梯度下降法拟合模型，predict_proba 方法返回预测概率，predict 方法返回分类结果，score 方法评估模型性能。

import numpy as np
from .metrics import accuracy_score  # 导入 accuracy_score 函数，用于评估模型性能

class LogisticRegression:
    """逻辑回归模型"""

    def __init__(self):
        """初始化Logistic Regression模型"""
        self.coef_ = None  # 系数（特征权重）
        self.intercept_ = None  # 截距（偏置）
        self._theta = None  # 内部参数 theta

    def _sigmoid(self, t):
        """定义 sigmoid 函数"""
        return 1. / (1. + np.exp(-t))

    def fit(self, X_train, y_train, eta=0.01, n_iters=1e4):
        """使用梯度下降法拟合模型"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"

        # 定义损失函数 J 和损失函数的梯度 dJ
        def J(theta, X_b, y):
            y_hat = self._sigmoid(X_b.dot(theta))
            try:
                return - np.sum(y*np.log(y_hat) + (1-y)*np.log(1-y_hat)) / len(y)
            except:
                return float('inf')

        def dJ(theta, X_b, y):
            return X_b.T.dot(self._sigmoid(X_b.dot(theta)) - y) / len(y)

        # 定义梯度下降函数
        def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):

            theta = initial_theta
            cur_iter = 0

            while cur_iter < n_iters:
                gradient = dJ(theta, X_b, y)
                last_theta = theta
                theta = theta - eta * gradient
                if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
                    break

                cur_iter += 1

            return theta

        # 添加偏置项，构建增广矩阵
        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        initial_theta = np.zeros(X_b.shape[1])  # 初始化参数
        # 使用梯度下降法求解模型参数 theta
        self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)

        # 提取截距和系数
        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

    def predict_proba(self, X_predict):
        """给定待预测数据集X_predict，返回表示X_predict的结果概率向量"""
        assert self.intercept_ is not None and self.coef_ is not None, \
            "must fit before predict!"
        assert X_predict.shape[1] == len(self.coef_), \
            "the feature number of X_predict must be equal to X_train"

        X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
        return self._sigmoid(X_b.dot(self._theta))

    def predict(self, X_predict):
        """给定待预测数据集X_predict，返回表示X_predict的结果向量"""
        assert self.intercept_ is not None and self.coef_ is not None, \
            "must fit before predict!"
        assert X_predict.shape[1] == len(self.coef_), \
            "the feature number of X_predict must be equal to X_train"

        proba = self.predict_proba(X_predict)
        return np.array(proba >= 0.5, dtype='int')

    def score(self, X_test, y_test):
        """根据测试数据集 X_test 和 y_test 确定当前模型的准确度"""

        y_predict = self.predict(X_test)
        return accuracy_score(y_test, y_predict)

    def __repr__(self):
        return "LogisticRegression()"

对鸢尾花数据集中类别为0和1的样本进行逻辑回归建模，并进行模型训练和预测。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

# 加载鸢尾花数据集，这里只使用数据的前两个特征
iris = datasets.load_iris()
X = iris.data
y = iris.target

# 只选择数据中类别为0和1的样本，并且仅取前两个特征
X = X[y < 2, :2]
y = y[y < 2]

# 绘制散点图，展示两个类别的数据分布
plt.scatter(X[y == 0, 0], X[y == 0, 1], color="red", label="0")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color="blue", label="1")
plt.xlabel("Feature 1")  # x轴标签
plt.ylabel("Feature 2")  # y轴标签
plt.legend()  # 添加图例
plt.show()

# 导入自定义的训练集划分函数 train_test_split
from playML.model_selection import train_test_split

# 划分训练集和测试集，设置随机种子为666
X_train, X_test, y_train, y_test = train_test_split(X, y, seed=666)

# 导入自定义的逻辑回归类 LogisticRegression
from playML.LogisticRegression import LogisticRegression

# 创建逻辑回归模型对象
log_reg = LogisticRegression()

# 使用训练集进行模型训练
log_reg.fit(X_train, y_train)

# 输出模型在测试集上的准确率
print(log_reg.score(X_test, y_test))

# 输出模型对测试集样本的预测概率
print(log_reg.predict_proba(X_test))

# 输出模型对测试集样本的分类预测结果
print(log_reg.predict(X_test))

逻辑回归的决策边界

决策边界是指在特征空间中将不同类别的样本分开的边界。由于逻辑回归是二分类算法，因此其决策边界是一个超平面，可以用一个线性方程表示。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from playML.model_selection import train_test_split
from playML.LogisticRegression import LogisticRegression

# 加载鸢尾花数据集，仅选择前两个特征，并且仅选择两个类别
iris = datasets.load_iris()
X = iris.data[:,:2]
y = iris.target
X = X[y < 2]
y = y[y < 2]

# 分割数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, seed=666)

# 创建并训练逻辑回归模型
log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)

# 定义一个函数来绘制决策边界
def plot_decision_boundary(model, axis):
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1, 1)
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]
    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

# 绘制决策边界
plot_decision_boundary(log_reg, axis=[4, 7.5, 1.5, 4.5])
plt.scatter(X[y==0,0], X[y==0,1], color="red")
plt.scatter(X[y==1,0], X[y==1,1], color="blue")
plt.show()

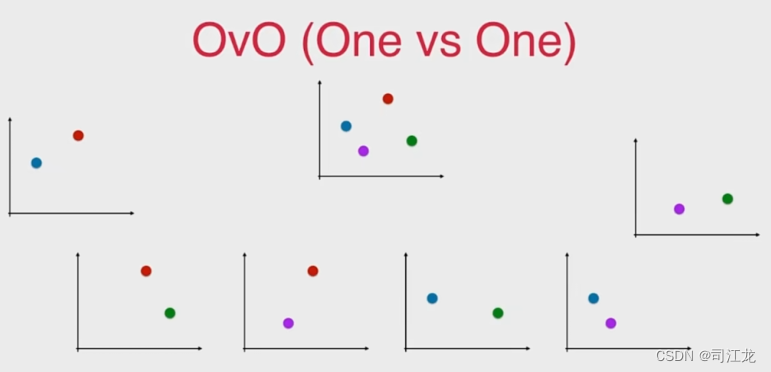
 多类分类问题策略OvR与OvO

十、支撑向量机SVM

什么是SVM

支持向量机的基本思想是找到一个最优的超平面来分隔不同类别的数据点。在二维空间中，这个超平面就是一条直线，而在更高维空间中，它可以是一个超平面。SVM的目标是找到离超平面最近的数据点，这些数据点被称为支持向量，它们决定了超平面的位置和方向。SVM试图最大化支持向量与超平面的距离，这个距离被称为间隔（margin），因此SVM也被称为最大间隔分类器。

 

 scikit-learn中的SVM实际使用

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

# 加载鸢尾花数据集
iris = datasets.load_iris()

# 获取特征和标签
X = iris.data
y = iris.target

# 仅保留前两个特征，并且只保留两类
X = X[y < 2, :2]
y = y[y < 2]

from sklearn.preprocessing import StandardScaler

# 特征标准化处理
standardScaler = StandardScaler()
standardScaler.fit(X)
X_standard = standardScaler.transform(X)

from sklearn.svm import LinearSVC

# 创建线性支持向量机模型并拟合数据
svc = LinearSVC(C=1e9)
svc.fit(X_standard, y)

def plot_svc_decision_boundary(model, axis):
    # 定义绘制决策边界函数
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]

    # 预测决策边界
    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])  # 自定义颜色地图
    
    # 绘制决策边界
    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

    w = model.coef_[0]
    b = model.intercept_[0]

    # w0*x0 + w1*x1 + b = 0
    # => x1 = -w0/w1 * x0 - b/w1
    plot_x = np.linspace(axis[0], axis[1], 200)
    up_y = -w[0] / w[1] * plot_x - b / w[1] + 1 / w[1]  # 上边界
    down_y = -w[0] / w[1] * plot_x - b / w[1] - 1 / w[1]  # 下边界

    # 确定边界在指定范围内
    up_index = (up_y >= axis[2]) & (up_y <= axis[3])
    down_index = (down_y >= axis[2]) & (down_y <= axis[3])

    # 绘制边界线
    plt.plot(plot_x[up_index], up_y[up_index], color='black')
    plt.plot(plot_x[down_index], down_y[down_index], color='black')

# 绘制决策边界
plot_svc_decision_boundary(svc, axis=[-3, 3, -3, 3])

# 绘制数据点
plt.scatter(X_standard[y == 0, 0], X_standard[y == 0, 1])
plt.scatter(X_standard[y == 1, 0], X_standard[y == 1, 1])

plt.show()

十一、决策树

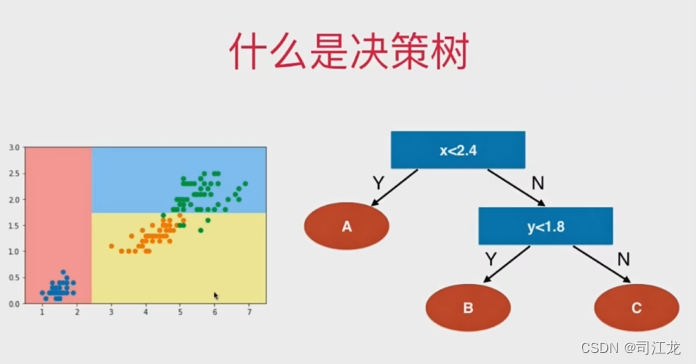
什么是决策树 

决策树（Decision Tree）是一种经常用于分类和回归任务的监督学习算法。它通过一系列的决策规则来学习数据的内在结构，以生成一个预测模型。 决策树的工作原理类似于人类的决策过程：从根节点开始，通过一系列问题对数据进行分割，每个问题都基于一个特征，直到达到叶节点，叶节点对应于一个类别（用于分类问题）或者一个数值（用于回归问题）。这样的决策路径形成了一个树状结构，因此称为“决策树”。

信息熵和基尼系数

信息熵（Entropy）和基尼系数（Gini Impurity）是用于衡量决策树中节点纯度的指标，通常用于特征选择和分割节点的决策。

1. 信息熵（Entropy）: 信息熵是一种用来度量数据集的纯度或不确定性的指标。对于二分类问题，假设数据集中正例的概率为$p$，负例的概率为$1-p$，则信息熵的计算公式为： H(p) = -p \log_2(p) - (1-p) \log_2(1-p)H(p)=−plog2​(p)−(1−p)log2​(1−p)

信息熵的取值范围在0到1之间。当数据集的纯度越高（即正例或负例占比越大），信息熵越低，达到最小值0。当数据集的正负例占比相等时，信息熵达到最大值1，表示最大的不确定性。

在决策树的构建过程中，信息熵用于衡量不同特征对数据集的划分效果，通常选择信息增益最大的特征来进行划分。

1. 基尼系数（Gini Impurity）: 基尼系数也是一种用来度量数据集纯度的指标，但与信息熵不同，基尼系数更加倾向于选择最常见的类别作为主要划分特征。

对于二分类问题，假设数据集中正例的概率为$p$，负例的概率为$1-p$，则基尼系数的计算公式为： Gini(p) = 1 - p^2 - (1-p)^2Gini(p)=1−p2−(1−p)2

基尼系数的取值范围也在0到1之间。与信息熵类似，基尼系数越低表示数据集的纯度越高，越倾向于某一类别。当数据集的正负例占比相等时，基尼系数取得最大值0.5。

在决策树的构建中，基尼系数常用于衡量特征的划分效果，通常选择基尼系数最小的特征作为划分节点。

 sklearn.tree的简单使用示例

# 导入必要的库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor

# 创建一个随机数据集
np.random.seed(0)
X = np.sort(5 * np.random.rand(80, 1), axis=0)
y = np.sin(X).ravel()
y[::5] += 3 * (0.5 - np.random.rand(16))  # 添加噪声

# 创建决策树回归模型
regressor = DecisionTreeRegressor(max_depth=5)

# 在训练集上拟合模型
regressor.fit(X, y)

# 预测
X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
y_pred = regressor.predict(X_test)

# 绘制结果
plt.figure()
plt.scatter(X, y, s=20, edgecolor="black", c="darkorange", label="data")
plt.plot(X_test, y_pred, color="cornflowerblue", linewidth=2, label="prediction")
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree Regression")
plt.legend()
plt.show()

十二、集成学习

 什么是集成学习

集成学习（Ensemble Learning）是一种机器学习方法，通过组合多个学习器来构建一个更强大和稳健的模型。集成学习的目标是将多个弱学习器（或基学习器）的预测结果进行组合，以产生比单个学习器更准确的预测结果。

集成学习的基本思想是“三个臭皮匠顶个诸葛亮”，即通过结合多个模型的意见来提高整体的性能。在集成学习中，通常有两种主要的方法：

1. Bagging（Bootstrap Aggregating）：Bagging通过随机有放回地从训练集中抽取多个子集，每个子集用于训练一个基学习器。然后，将所有基学习器的预测结果进行平均或投票来得到最终的预测结果。例如，随机森林（Random Forest）就是一种基于Bagging思想的集成学习方法。

2. Boosting：Boosting是一种迭代的集成学习方法，它通过顺序训练多个基学习器，每个学习器都根据前一个学习器的表现进行调整，以提高整体性能。Boosting的常见算法包括AdaBoost、Gradient Boosting等。

集成学习的优势在于它能够利用多个学习器之间的互补性，从而提高模型的泛化能力和鲁棒性。同时，集成学习也可以减少过拟合的风险，尤其是在基学习器的性能较差或数据噪声较多的情况下。因此，集成学习在实际应用中得到了广泛的应用，特别是在数据挖掘、分类、回归等领域。

Voting Classifier 和 Soft Voting Classifier 

Voting Classifier 和 Soft Voting Classifier 都是集成学习中的一种技术，用于将多个基础学习器的预测结果结合起来，以获得更好的整体预测效果。它们都属于集成学习中的投票法（Voting）。

1. Voting Classifier: Voting Classifier 是一种硬投票方法，它通过简单的多数投票来决定最终的预测结果。具体来说，它将每个基础学习器的预测结果进行投票，然后选择得票最多的类别作为最终的预测结果。在分类问题中，如果是二分类问题，则通常会选择概率值大于0.5的类别。在回归问题中，通常会选择预测值的平均值作为最终预测结果。

2. Soft Voting Classifier: Soft Voting Classifier 也是一种投票方法，但与硬投票不同的是，它考虑了每个基础学习器预测的概率值。具体来说，Soft Voting Classifier 将每个基础学习器预测的类别概率进行加权平均，然后选择加权平均概率最高的类别作为最终的预测结果。这样做可以更好地利用基础学习器的预测置信度信息。

Voting Classifier 和 Soft Voting Classifier 在实践中都有广泛的应用。它们可以结合不同的机器学习算法（如决策树、支持向量机、逻辑回归等）来构建集成模型，并通常能够提高整体模型的性能和鲁棒性。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.ensemble import VotingClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score

# 加载示例数据集（鸢尾花数据集）
iris = load_iris()
X, y = iris.data, iris.target

# 划分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建基分类器
log_clf = LogisticRegression(random_state=42)
rnd_clf = RandomForestClassifier(random_state=42)
svm_clf = SVC(probability=True, random_state=42)

# 创建 Voting Classifier（硬投票）
voting_clf_hard = VotingClassifier(
    estimators=[('lr', log_clf), ('rf', rnd_clf), ('svc', svm_clf)],
    voting='hard'
)

# 创建 Voting Classifier（软投票）
voting_clf_soft = VotingClassifier(
    estimators=[('lr', log_clf), ('rf', rnd_clf), ('svc', svm_clf)],
    voting='soft'
)

# 在训练集上拟合 Voting Classifier（硬投票）
voting_clf_hard.fit(X_train, y_train)

# 在测试集上进行预测并评估性能（硬投票）
y_pred_hard = voting_clf_hard.predict(X_test)
accuracy_hard = accuracy_score(y_test, y_pred_hard)
print("Voting Classifier（硬投票）的准确率：", accuracy_hard)

# 在训练集上拟合 Voting Classifier（软投票）
voting_clf_soft.fit(X_train, y_train)

# 在测试集上进行预测并评估性能（软投票）
y_pred_soft = voting_clf_soft.predict(X_test)
accuracy_soft = accuracy_score(y_test, y_pred_soft)
print("Voting Classifier（软投票）的准确率：", accuracy_soft)

 这段代码中，我们使用了逻辑回归、随机森林和支持向量机三种不同的基分类器，创建了 Voting Classifier。然后我们分别进行硬投票和软投票的方式来组合这些基分类器的预测结果，并进行性能评估。

Bagging 代码示例 

from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

# 加载示例数据集（鸢尾花数据集）
iris = load_iris()
X, y = iris.data, iris.target

# 划分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 使用BaggingClassifier包装决策树分类器，构建 Bagging 集成模型
# 参数解释：
#   - base_estimator：基学习器，这里使用决策树分类器作为基学习器
#   - n_estimators：集成模型中基学习器的数量
#   - max_samples：每个基学习器所采样的样本数量，这里设置为100
#   - bootstrap：是否采用有放回抽样，即是否允许样本重复采样
bagging_clf = BaggingClassifier(DecisionTreeClassifier(),
                                n_estimators=500, max_samples=100,
                                bootstrap=True)

# 在训练集上拟合 Bagging 集成模型
bagging_clf.fit(X_train, y_train)

# 在测试集上评估模型性能
accuracy = bagging_clf.score(X_test, y_test)
print("Bagging Classifier（n_estimators=500）的准确率：", accuracy)

# 调整 n_estimators 参数为 5000
bagging_clf = BaggingClassifier(DecisionTreeClassifier(),
                                n_estimators=5000, max_samples=100,
                                bootstrap=True)

# 在训练集上拟合 Bagging 集成模型
bagging_clf.fit(X_train, y_train)

# 在测试集上评估模型性能
accuracy = bagging_clf.score(X_test, y_test)
print("Bagging Classifier（n_estimators=5000）的准确率：", accuracy)