基本概念
微积分是数学中的一个主要分支,专注于研究函数、极限、导数、积分等的理论。它是现代科学和工程中不可或缺的基础工具,尤其在处理变化率和累积量的问题时显得尤为重要。微积分通常分为两大部分:微分学和积分学。
微分学
微分学关注的是函数的局部行为,即如何衡量函数在某一点附近的变化率。
- 导数:

- 高阶导数:函数的导数本身也可以是一个函数,我们可以继续求这个导数函数的导数,称为二阶导数。同理,还有三阶导数、四阶导数等。
- 应用:微分学的概念和方法被广泛应用于物理学、工程学、经济学、生物学等领域,用于研究速度、加速度、斜率、优化问题等。
积分学
积分学主要研究的是如何计算函数图形下的面积,以及更一般的累积量问题。
- 不定积分:
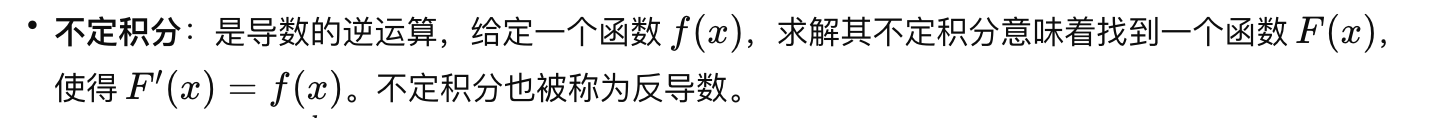
- 定积分:

- 应用:积分学用于计算面积、体积、累积变化量等,广泛应用于物理学(如计算位移、工作和能量)、经济学(如消费者和生产者剩余)、生态学等领域。
微积分在AI中的应用
在人工智能(AI)领域,微积分的应用主要集中在优化问题和模型训练上:
- 梯度下降:梯度下降是一种用于寻找函数最小值的优化算法,广泛用于机器学习和深度学习模型的训练。该方法利用函数的导数(梯度)来确定搜索的方向。
- 反向传播算法:在训练深度神经网络时,反向传播算法通过计算损失函数对每个权重的偏导数来更新网络中的权重,这一过程本质上是微分的应用。
总之,微积分为我们提供了一种强大的工具来理解和建模连续变化,它在科学研究、工程设计、经济分析以及AI技术的发展中都扮演着关键角色。
微积分在AI中的应用
偏导数和梯度
在人工智能(AI)尤其是在机器学习和深度学习中,偏导数和梯度的概念是理解和实施优化算法的基础。它们在神经网络训练的核心算法——梯度下降法中扮演着至关重要的角色。
偏导数
当我们处理的函数有多个自变量时,对其中一个自变量求导数,而保持其他自变量不变的导数,称为偏导数。偏导数衡量了在多维空间中,函数沿着某一个维度的变化率。

梯度

梯度下降法
梯度下降法是一种用来寻找函数最小值的优化算法。在神经网络训练中,梯度下降法用来最小化损失函数,即找到使损失函数取得最小值的参数(例如权重和偏置)。
具体来说,梯度下降法通过以下步骤迭代更新参数:
- 计算损失函数关于每个参数的梯度,即找到损失函数在当前参数点上的导数。
- 更新参数,使其沿梯度的反方向移动一小步,因为梯度指向的是函数增加最快的方向,所以反方向通常可以减少函数的值。参数更新公式为:θ=θ−α∇f(θ),其中 α 是学习率,决定了更新的步长。
在AI中的应用
梯度下降和偏导数在AI中的应用不仅限于神经网络的训练。在任何需要优化的场景,比如调整算法的超参数、最大化某个性能指标(如精确度)或最小化代价函数等,梯度下降法都是一个重要的工具。通过计算梯度,我们可以高效地找到函数的极值点,这对于训练高效、准确的机器学习模型至关重要。
积分
积分在人工智能(AI)领域,特别是在涉及概率论和连续变量建模的场景中,发挥着重要作用。积分可以帮助我们理解变量的累积效应,计算总量或平均值,以及在连续空间内建模变量的行为。以下是积分在AI中的一些关键应用:
计算累积分布函数(CDF)
累积分布函数(CDF)是概率论中一个基本概念,表示一个随机变量小于或等于某个值的概率。对于连续随机变量,CDF是概率密度函数(PDF)的积分。通过积分PDF,我们可以得到CDF,进而了解随机变量的分布特性。这在统计分析和机器学习模型评估中非常有用,例如,通过CDF可以计算变量落在某个区间内的概率,或者进行分位数估计。
模拟连续变量的行为
在许多AI算法中,特别是在涉及连续空间优化的问题中,积分可以用来模拟和分析连续变量的行为。例如:
- 贝叶斯统计:在贝叶斯统计中,积分用于计算边缘概率分布,即通过对复合概率分布进行积分,来消除(或“边缘化”)一些变量的影响。这在贝叶斯推理中是核心操作,帮助我们根据观测数据更新对未知参数的信念。
- 期望值和方差的计算:积分在计算连续随机变量的期望值(即平均值)和方差(衡量分散度)时起到关键作用。期望值是随机变量乘以其概率密度的积分,而方差则涉及到随机变量与其期望值差的平方的积分。
优化问题
在优化问题中,特别是当目标函数或约束条件以连续形式给出时,积分可以用来求解问题的最优解。例如,在控制理论和强化学习中,积分常用于求解连续时间动态系统的最优控制策略。
函数逼近
在机器学习和深度学习中,积分有时被用来进行函数逼近。例如,神经网络的训练可以视为在函数空间中寻找一个最佳函数,该函数最小化某种损失函数。在处理连续输入或输出空间的问题时,积分有助于估计这些函数的性能指标。
结论
积分作为微积分中的一个基本概念,在AI领域有广泛的应用,特别是在处理概率分布、优化问题和连续变量建模时。通过积分,我们能够更深入地理解和分析AI算法的行为和性能,从而设计出更高效、更准确的模型。