最近学校作业有点多+被迫参加学校的仪仗队当帕鲁，有许多题还没有补（尤其是牛客，寒假时没有怎么管，现在后悔了qaq),蓝桥杯也快来了，一下子事情多了起来，反而不知道要看什么了，在此先立个flag----蓝桥杯拿个奖（能省一最好，没有的话省2/3也不是不行）        

同时写一下近期计划：到4月前把寒假的题补完，到4月10号前刷完真题。

进入正题：

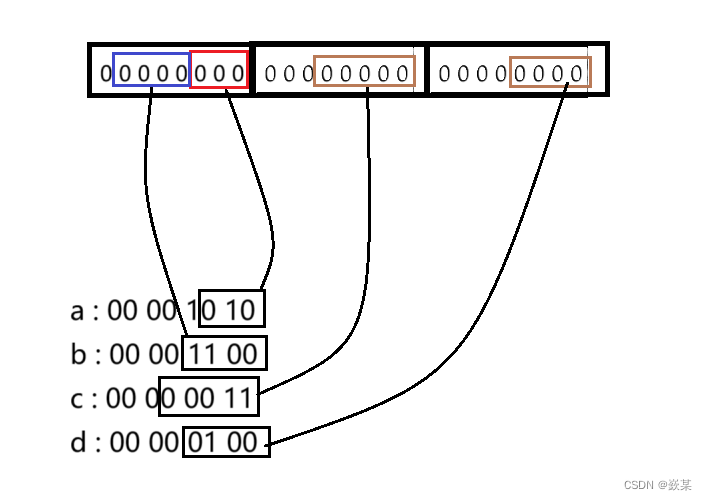
什么是0/1trie? 就是一个二叉树，左节点为0，右节点为1，因此，某一个数的二进制从高位到低位可以用0/1trie从根节点往下走写出。

下面让我们直接看题吧：

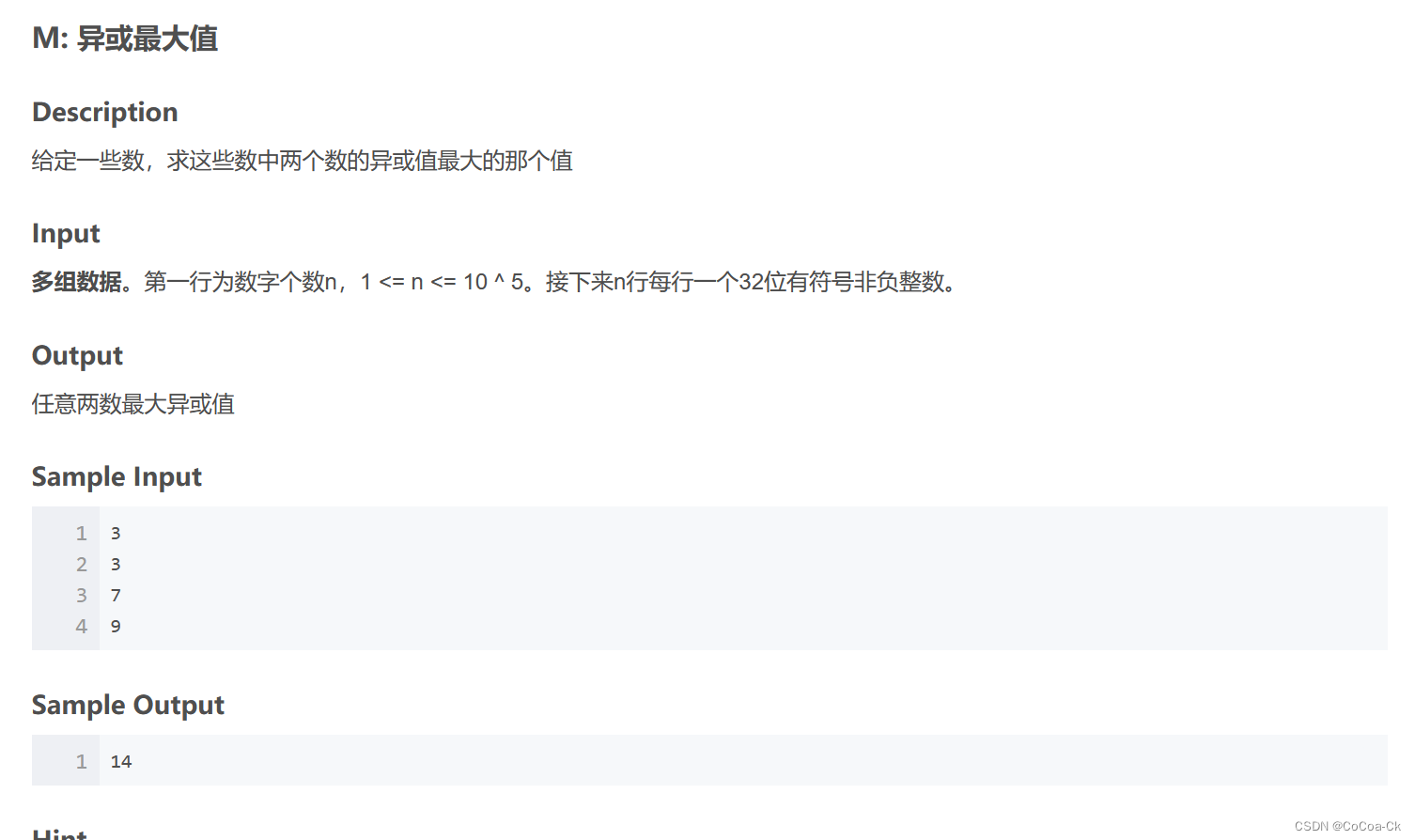
直接枚举的话复杂度为n^2,因此我们考虑用0/1trie，我们先枚举数，然后如果有不同的位就选它即可，下面是AC代码（可以当模板记）：

#include<bits/stdc++.h>
using namespace std;
const int N=100010;
int n,a[N];
int ch[N*31][2],idx;
void insert(int x){
	int p=0;
	for(int i=30;i>=0;i--){
		int j=(x>>i)&1;
		if(ch[p][j]==0) ch[p][j]=++idx;
		p=ch[p][j];
	}
}
int query(int x){
	int p=0,res=0;
	for(int i=30;i>=0;i--){
		int j=(x>>i)&1;
		if(ch[p][!j]){
			res+=(1<<i);
			p=ch[p][!j];
		}
		else p=ch[p][j];
	}
	return res;
}
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		insert(a[i]);
	}
	int ans=0;
	for(int i=1;i<=n;i++){
		ans=max(ans,query(a[i]));
	}
	cout<<ans;
}

来个比较难的（出自寒假训练营2）

首先，我们只要考虑最大值与最小值，于是我们sort一下，当我们把相应的i与j确定后，中间的数相当于都可以有选与不选，因此为2^(j-i-1)种，现在问题就转化成了如何求符合的max,min对，我们不妨先枚举max,我们同时构造0/1trie,我们知道：

1.如果k的一位为0，那么max^min为1的话他的子树都可以选。

2.若k的一位为1，那么max^min只能选1.

因此，我们让其走下去不断累加答案，至于一个串贡献的方案数，我们2^(j-i-1)=2^(j-1)/2^i,于是我们在树上用逆元维护1/2^i即可。

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10,mod=1e9+7;
long long son[10000100][2],w[10000100],idx;
long long n,k,a[N];
bool cmp(int a,int b){
    return a<b;
}
long long qpow(long long a,long long b){
    long long res=1;
    while(b){
        if(b&1) res=res*a%mod;
        a=a*a%mod;
        b>>=1;
    }
    return res;
}
void insert(long long x,long long id){
    long long p=0,inv=qpow(qpow(2,id),mod-2);
    for(int i=30;i>=0;i--){
        int u=(x>>i)&1;
        if(son[p][u]==0) son[p][u]=++idx;
        p=son[p][u];
        w[p]=(w[p]+inv)%mod;
    }
}
long long quary(long long x){
    long long res=0,p=0;
    for(int i=30;i>=0;i--){
        int u=(x>>i&1)^(k>>i&1);
        if(k>>i&1) res=(res+w[son[p][1-u]])%mod;
        if(son[p][u]==0) return res;
        p=son[p][u];
    }
    return (res+w[p])%mod;
}
void solve(){
    cin>>n>>k;
    for(int i=0;i<=idx;i++){
        son[i][0]=0;
        son[i][1]=0;
        w[i]=0;
    }
    idx=0;
    for(int i=1;i<=n;i++) cin>>a[i];
    sort(a+1,a+n+1,cmp);
    long long ans=0;
    for(int i=1;i<=n;i++){
        ans=(ans+quary(a[i])*qpow(2,i-1)%mod+1)%mod;
        insert(a[i],i);
    }
    cout<<ans;
    return;
}
int main(){
    ios::sync_with_stdio(false),cin.tie(nullptr);
    int t;
    cin>>t;
    while(t--){
        solve();
        cout<<endl;
    }
}