二、唯一解码器模型入门 — 因果语言建模

        Decoder only Model：唯一解码器，指摒弃词汇中一词多意，指向唯一概念。

        目标是预测词汇量的分布，我们可以看看是否可以使用转换器作为函数来预测这种分布。

为此，我们可以考虑 3 种可能性：

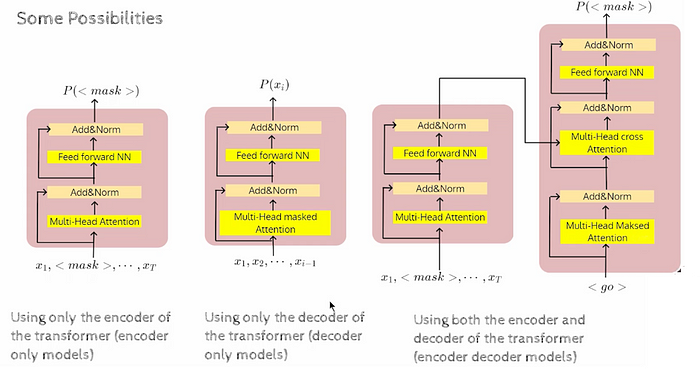
三、唯一解码器的型号有哪些？

        这就是香草解码器模型如何具有自注意力、交叉注意力和前馈网络。

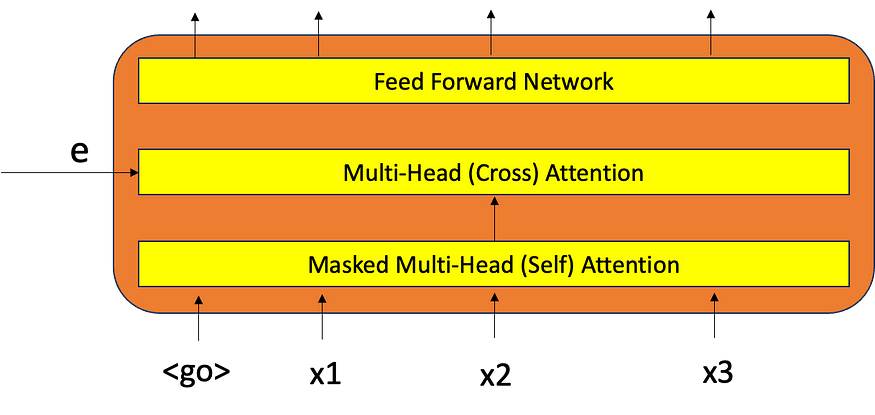
        输入是一个单词序列，其中给定的 k 个单词将用于预测 k+1 个单词，这是语言建模的基本任务。这个 k 可以从 0 开始，即，如果我们没有得到任何单词，那么它将以 <go> 开头并预测第一个单词，给定第一个单词，我们预测第二个单词，它像这样迭代，直到任务完成。在这里，我们希望模型只看到现在和过去的输入。我们可以通过应用掩码并将所有未来单词的权重归零来实现这一点。

        在训练过程中，我们实际上拥有所有数据，其中整个文档和整个段落，我们假设我们想要预测第 5 个单词——预测第 5 个单词之后的内容是没有意义的，因为之后是模型要预测的任务，它必须首先生成第 5 个单词，然后获取 5 个单词并生成第 6 个单词——如果我们已经假设会发生什么在第 5 个单词之后，预测第 5 个单词的任务将变得更加容易，在现实世界中，当使用模型时，它将无法访问第 6、7 或第 8 个单词，因为我们希望用户给出提示并完成以下句子“我要”，然后它就停止了，它不会给你其余的上下文。在训练时，我们可以自由地了解整个上下文和整个段落，但我们必须解决这个问题。我们不能利用这种自由，我们必须放弃这些信息。因此，我们只能查看现在和过去的输入——我们可以通过应用掩码来实现这一点，所以当我们计算剩余元素的注意力时，我们只是像往常一样做所有事情，但最后当我们试图计算注意力权重时，我们只是应用掩码并将所有未来单词的权重归零， 这就像说我们将对 i = 1 到 T（序列长度）进行求和一样好。所以现在新的第 j 个表示包含所有关键字，我们不需要所有关键字，而只想要我们被允许看到的前 k 个单词。因此，对于所有其他剩余的 i，我们将使所有 alpha 为 0。如何在数学上做到这一点，我们添加了掩码矩阵，它包含-无穷大，可以确保秤数变为 0。

        这个求和方程不是所有 T 元素的总和，而是我们只想通过使所有其他元素的 alpha 为 0 来对第一个“k”元素求和——这就是掩码概念的全部内容。

        我们可以通过应用掩码矩阵来实现这一点。屏蔽多头注意力层是必需的，但我们不需要任何交叉注意力，因为这里我们只处理仅解码器模型，这里没有编码器概念。这就是仅解码器模型的样子。

        输出表示链式规则中的每个术语，因此第一个实例是预测任何采用任何 V 单词词汇表的任何单词的第一个单词分布的概率。

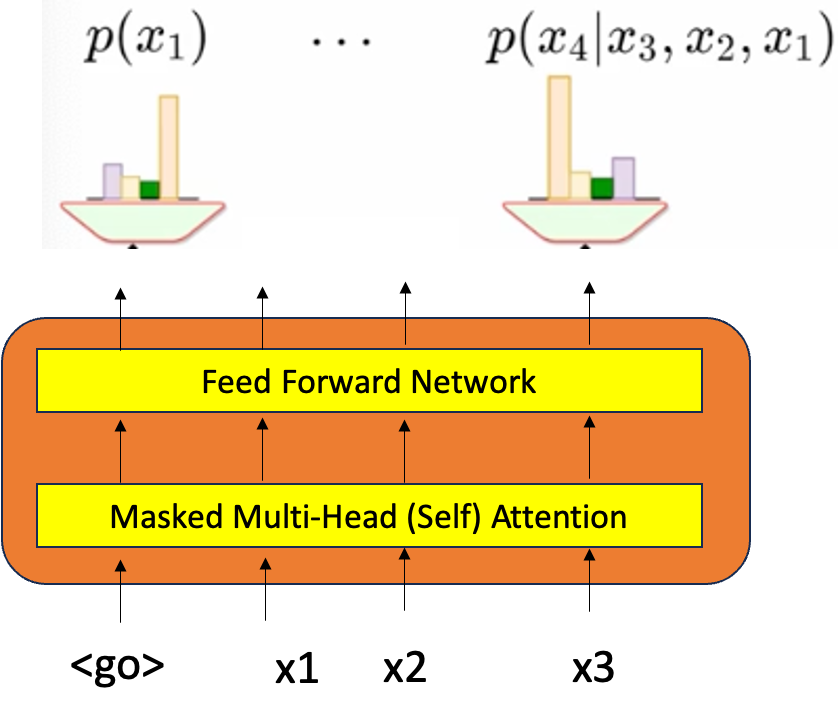
        P（x1） 是一个边际分布，它不以任何条件为条件，它只是一个第一个词。在每个阶段，我们都在预测词汇的分布。然而，这一次的概率是由模型的参数决定的，即，假设 trasformer 中的所有参数（如 W、Q、V 和 FFN 的参数）都给定了，我们假设它们是 Theta 的一部分。 现在，如果给定带有 3 个单词 （go， I， am） 的输入和 （I， am） 的嵌入 （n dim） 也被训练并且是 theta 的一部分，并且确实传递到转换器中，并且还进行了某种计算，从而产生带有 softmax 的输出。这给出了变压器使用变压器的参数计算的概率分布。

        因此，目标是最大化似然 L（theta）。因此，如果我们使用第一个单词<go>那么第一个概率输出单词必须以 P（I） 为最大值，现在当我们将“I”作为第二个单词作为输入时，概率 P（x2 = am/x1= I） 必须最大化。这是一个迭代反向传播算法，我们将不断调整参数 theta，直到在一段时间内，概率开始对齐，实际上希望它们对齐，最后正确的词获得最大概率。

        现在让我们来看看生成式预训练转换器 （GPT） 模型的外观——现在我们可以创建一个经过修改的去码器层（称为 transformer 块）的堆栈 （n）。设 X 表示输入序列

        现在让我们看一下类似的东西：

• 训练所依据的数据？
• 架构 — 有多少个维度？有多少注意力头？计算参数总数？

四、输入数据规模（来自图书语料库）

• 它包含 7000 本独特的书籍、7400 万个句子和大约 10 亿个单词，涵盖 16 种类型。
• 此外，它还使用长距离连续文本（即，没有句子或段落的洗牌）。
• 序列长度“T”是 512 个标记或上下文大小，并且是连续的。
• 它有一个分词器，即字节对编码。
• 词汇量为40478个单词。
• 嵌入维度为 768

模型

• 包含 12 个解码器层（变压器模块）
• 上下文大小：512 → 512 个输入/令牌一次 （T）
• 注意头 ： 12
• 前馈网络层大小：768 x 4 倍 = 3072
• 激活： 高斯误差线性单元 （GELU）

        这种激活来自 FFN，它们使用 Dropout、层归一化和残差连接来实现，以增强训练期间的收敛性。FFN 将采用 768 维输出，该输出由 12 个注意力头 （64 x 12） 计算得出，其中每个头产生 64 维输出并连接以获得与每个令牌的输入维度大小相匹配的 768 维输出。因此，这些变压器块中的每一个都将提供 768 维的输出，但在每个具有 FFN 的变压器块之间转换为 768 x 4 = 3072 并转换或缩小回 768 维输出。

        我们以 512 个代币的样本输入数据为例（假设数据以空格作为拆分为代币的标识符）

        如果我们将整个 512 个令牌输入给 transformer 块，每个令牌都有相应的词嵌入。此输入将是 T x d 模型，即 768。每个嵌入的大小为 768 或 dmodel，我们有 T 个这样的嵌入。所以输入大小是 T x dmodel，所以对于每一层，我们将有 T x dmodel 输出，直到最后一层，在最后一层，我们转换为 softmax，我们将预测 T 概率分布。这都是应用的掩码，因此我们能够并行执行所有这些过程，并且我们确保在每个阶段我们都不会着眼于未来，并且所有概率都是并行产生的。

        这就是一个训练批次（批次大小 = 1）的样子，其中包含 512 个令牌，该令牌被传递到第一个 transformer 块中，然后传递到多头掩码注意，然后转到 FFN。

        让我们看看多头蒙面注意力是什么样子的。第一个头将获取所有这些 512 个标记，它将生成 Q、K、V 向量并执行整个操作，直到 MatMul 并再次给出 512 个向量。每个向量的大小将为 dmodel/#heads = 768/12 = 64。因此，它产生每个单独的磁头输出，然后连接以获得 768 输出大小。

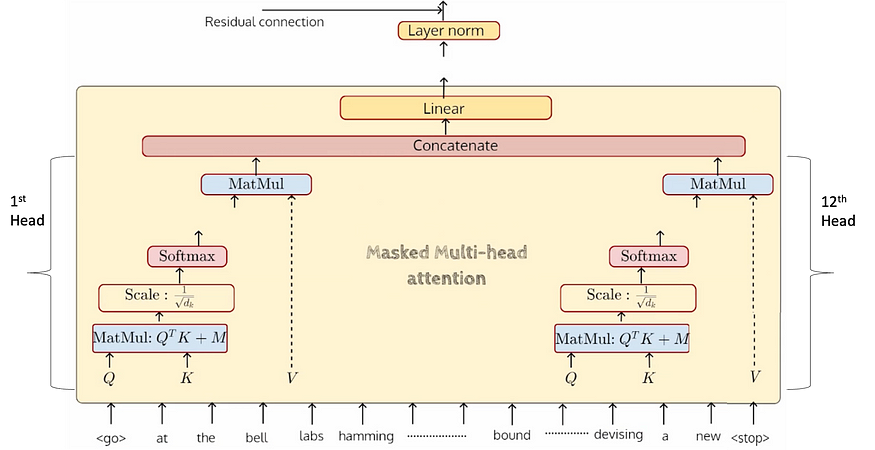
        所有 12 个磁头输出并行生成，以产生 64 维向量，然后连接到 768 维输出。因此，这将发生在所有 512 个输入令牌上。最后，我们得到这样的 512 x 768 向量，输入数将与输出数相同，并且每一层都相同。所以我们有一个 512 x 768 的输入，它进入了屏蔽的注意力，并给出了 512 x 768 的输出。这 768 个输出中的每一个都进入了线性变换，这在某种程度上完成了一个蒙面多头注意力的周期。此时，我们得到了所有 512 个新表示，每个表示的大小为 768。

        在添加一个 dropout 层并查看残差连接是如何传递的（基本上从原始输入流出）后，我们得到了一个 H1 = X + H 的输出，它的大小同样是 512 x 768，它应该传递到 FFN，让我们看看它是什么样子的。

        现在，所有 768 大小的 512 个代币都将进入 FFN 并产生 3072 个中间 vecrtor 大小，然后再次生成最终的 768 大小向量。因此，同样，这将对所有 512 个代币完成。下图仅针对其中一个令牌以及传递到隐藏层的 GELU 激活完成。

如上所示，这是网络输出的一个块的样子。

回顾一下到目前为止发生的事情：

• 取一大块连续的文本，即 512 个标记
• 将其馈送到变压器层和每一层，我们再次产生 512 个输出，直到最后一层
• 在最后一层，我们应用 softmax 将其转换为 512 个概率，即 P（x1）、P（x2/x1）、P（x3/x1，x2）...........P（x512/x1，x2，x3...x511）
• 所有这些预测都是同时发生的，而面具确保我们看不到任何未来的词语，或者看不到的词语

现在让我们检查一下参数的数量：

token 嵌入 ： |v|x Embedding_dimension

= 40478 x 768 = 31 x 10⁶ = 31M

~40K 单词中的词汇和 dmodel 是 768 个维度。

位置嵌入 ：上下文长度 x embedding_dimensions

= 512 x 768 = 0.3 x 10⁶ = 0.3M

总计 = 仅在输入层中提供 31.3 M 个参数（嵌入和位置嵌入）

位置嵌入也是学习的，这与原始变压器不同，原始变压器使用固定正弦嵌入来编码位置。

        对于注意力参数，我们有 3 个矩阵 Wq、Wk 和 Wv，每个矩阵接受 768 维输入并转换为 64 维输出，因此矩阵将是 768 x 64 — 这是每个注意力头，我们有 3 个这样的矩阵，因此 3 x （768 x 64） ~ 147 x 10³。所以我们有 12 个这样的头，因此参数将是 12 x 147 x 10³ ~ 1.7M。然后考虑一个线性层，其中我们有 768 维，这是一个串联的输出 （64 x 12），乘以 Wo（768 x 768 维）得到 768 向量 — 768 x 768 ~ 0.6M。因此，最后，对于所有 12 个块，在所有层中总和的蒙面多头自注意力存在 ~27.6M 参数。

        分别为 3072 和 768 的偏差以及 2 x （768 x 3072） 将最终给出 FFN 参数，一个块的总和为 4.7M。因此，当对所有 12 个块进行时，它是 12 x 4.7 ~ 56.4M

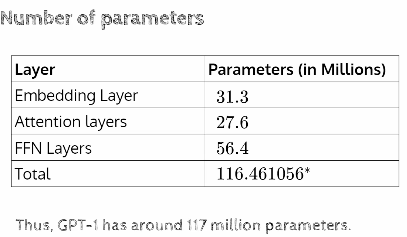
        在完整的变压器结束时，我们将获得 768 维尺寸输出，该输出再次转换为 40478 尺寸，我们需要 768 x 40478 矩阵才能获得 40478 尺寸。初始输入嵌入矩阵的大小为 40478 x 768。这些输入和输出矩阵可以共享，因此它们不作为参数包含在内。

        与目前市场上的 SOTA 模型相比，该 GPT-1 模型的参数较少。