王道机试C++续第6章数学问题贪心算法和蓝桥杯真题Day37倒计时24天

6.4 分解质因数

上一节讨论了素数的问题，而素数常用于分解质因数。每个数都可以写成一个或几个质数相乘的形式，其中每个质数都是这个数的质因数。把一个数用质因数相乘的形式表示出来，就称为分解质因数。例如，对一个数 x 分解素因数就是确定素数 p 1 , p 2 ,… , p n ，使其满足

质因数是指能够整除给定正整数的质数。换句话说，如果一个正整数n能够被另一个正整数x整除，而x是一个质数，那么我们称x是n的一个质因数。

举个例子，对于数字12来说，它可以被2、3和6整除，其中2和3都是质数，所以12的质因数可以表示为2和3。

例质因数的个数（清华上机）

题目描述：

求正整数 N （ N > 1 ）的质因数的个数。相同的质因数需要重复计算。例如， 120 = 2× 2× 2× 3× 5 ，

共有 5 个质因数。

输入：可能有多组测试数据，每组测试数据的输入是一个正整数 N （ 1 < N < 10^ 9 ）。

输出：对于每组数据，输出 N 的质因数的个数。

样例输入：

120

样例输出：

代码表示：

#include <bits/stdc++.h>
using namespace std;
//用于存储小于等于1e9的整数的平方根的整数部分
const int MAXN = sqrt(1e9) + 1;
vector<int> prime; //保存质数
bool isPrime[MAXN]; //标记数组
//初始化isPrime数组
void Initial() {
    for (int i = 0; i < MAXN; ++i) { //初始化
        isPrime[i] = true;
    }
    isPrime[0] = false;
    isPrime[1] = false;
    
//找出小于MAXN的所有质数并存储在prime向量中   
    for (int i = 2; i < MAXN; ++i) {
        if (!isPrime[i]) { //非质数则跳过
            continue;
        }
        prime.push_back(i);//找到了一个新的质数添加到prime 
        
        for (int j = i * i; j < MAXN; j += i) {
            isPrime[j] = false; //质数的倍数为非质数
        }
    }
    return ;
}

int main() {
    Initial();
    int n;
    while (scanf("%d", &n) != EOF) {
        int answer = 0;
//这个for循环的作用是遍历prime向量中的质数根据当前质数与n的关系
//来控制循环的执行只有当前质数小于n时才进行质因数的判断和计算
        for (int i = 0; i < prime.size() && prime[i] < n; ++i) {
        	//prime向量中第i个质数赋值给factor，作为当前质因数。
            int factor = prime[i];
            while (n % factor == 0) { 
                n /= factor;//不断试除
                answer++;//质因数个数加1
            }
        }
        
    //如果n大于1，说明剩余的n本身就是一个质因数。
        if (n > 1) { //还存在一个质因数
            answer++;
        }
        printf("%d\n", answer);
    }
    return 0;
}

6.5 快速幂

例人见人爱 A^B

题目描述：

求 A^B 的最后三位数表示的整数。说明： A^B 的含义是“ A 的 B 次方”。

输入：输入数据包含多个测试实例，每个实例占一行，由两个正整数 A 和 B 组成（ 1 <= A,B <=

10000 ）。如果 A=0 ， B=0 ，则表示输入数据的结束，不做处理。

输出：对于每个测试实例，请输出 A^B 的最后三位表示的整数，每个输出占一行。

样例输入：

2 3

12 6

6789 10000

0 0

样例输出：

984

代码表示：

#include <bits/stdc++.h>
using namespace std;
int main() {
    int a, b;
    while (cin >> a >> b) {
        if (a == 0 && b == 0) {
            break;
        } else {
            long long num = 1;
            for (int i = 1; i <= b; ++i) {
                num *= a;
            }
            cout << num % 1000 << endl;
        }
    }
    return 0;
}

第 7 章贪心策略

程序设计中非常重要的一种思想——贪心策略。贪心策略常用于求解最优化问题，核心思想是，总是选择当前状态下最优的策略。并不以整体最优进行考虑，而只考虑当前这一步。因此，这种方法能够得到局部最优解，最后往往也能够获得全局较优解，但并不保证收敛到全局最优解。

对于特定的最优化问题，贪心策略保证一定能够保证收敛到全局最优解。这类最优化问题具备无后效性，即某个状态以前的过程不会影响以后的状态，而只与当前状态有关。只要最优化问题具有这样的性质，便能保证使用贪心策略一定能够获得最优解。

7.1 简单贪心

例鸡兔同笼（北大复试）

题目描述：

一个笼子里面关了鸡和兔子（鸡有 2 只脚，兔子有 4 只脚，没有例外）。已知笼子里面脚的总数

是 a ，问笼子里面至少有多少只动物，至多有多少只动物。

输入：每组测试数据占 1 行，每行一个正整数 a （ a < 32768 ）。

输出：输出包含 n 行，每行对应一个输入，包含两个正整数，第一个是最少的动物数，第二个是最多的动物数，两个正整数用一个空格分开。若没有满足要求的答案，则输出两个 0 。

样例输入：

样例输出：

0 0

代码表示：

#include <bits/stdc++.h>
using namespace std;

int main() {
    int a;
    while(cin >> a){
        if(a % 2 != 0){
            cout << "0" << " " << "0" << endl;
        }
        else if(a==2){
            cout <<"1"<< " " <<"1"<< endl;
        }
        else if(a%2==0&&a%4!=0){
        	cout <<a/4+(a-(a/4)*4)/2<<" "<<a/2<<endl;
		}
        else if(a%4==0){
            cout << a/4 << " " << a/2 << endl;
        }
    }
    return 0;
}

心得体会

一定要注意所有的情况，所以下面我们看看别人家的代码

#include <bits/stdc++.h>
using namespace std;

int main() {
    int a;
    while (cin >> a) {
        int minimum = 0;
        int maximum = 0;
        
        if (a % 2 == 0) { // 只有偶数才有解
            minimum = a / 4 + (a % 4) / 2;
            maximum = a / 2;
        }       
        cout << minimum << " " << maximum << endl;
    }
    return 0;
}

例股票买卖 II

题目描述：

给定一个长度为 N 的数组，数组中的第 i 个数字表示一个给定股票在第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

输入格式：

第一行包含整数 N，表示数组长度。

第二行包含 N 个不大于 10000 的正整数，表示完整的数组。

输出格式：输出一个整数，表示最大利润。

数据范围：1≤N≤105

输入样例1：

6
7 1 5 3 6 4
输出样例1：7

输入样例2：

5

1 2 3 4 5

输出样例2：4

输入样例3：

5

7 6 4 3 1

输出样例3：0

解释：

样例1：在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。共得利润 4+3 = 7。

样例2：在第 1 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

样例3：在这种情况下, 不进行任何交易, 所以最大利润为 0。

思路提示：这道题目中最优解的方案可能不止一个。我们看样例1，是后一天比前一天股票价格大的时候我们把股票买入，同时在后一天卖出。这样就能获得利润。我们再看样例2，是在第一天买入，第五天卖出。我们可以把它拆解成四小段，也就是前一天买入，后一天卖出。结果是一样的。因此，我们可以想到任何一大段时间的股票买卖都可以拆解成很多段两天的股票买卖。当转换为两天的股票买卖时，我们只需要考虑是否盈利就行（如样例1的分析）。只要找到没两天的盈利相加就是最大盈利值。

代码表示：

#include <bits/stdc++.h>
using namespace std;

const int N=1e5+10;
int n;
int price[N];
int main()
{
    scanf("%d",&n);
    
    for(int i=0;i<n;i++)
    {
        scanf("%d",&price[i]);
    }
    
    int res=0;
    for(int i=0;i<n-1;i++)
    {
        if(price[i]<price[i+1])
            res+=price[i+1]-price[i];
    }
    
    printf("%d",res);
    return 0;
}

例仓货选址

题目描述：

在一条数轴上有 N 家商店，它们的坐标分别为 A1∼AN。现在需要在数轴上建立一家货仓，每天清晨，从货仓到每家商店都要运送一车商品。为了提高效率，求把货仓建在何处，可以使得货仓到每家商店的距离之和最小。

（每家都要送一家所以送完一家要回去到货舱取货送下一家）

输入格式：

第一行输入整数 N。

第二行 N 个整数 A1∼AN。

输出格式：输出一个整数，表示距离之和的最小值。

数据范围：

1≤N≤100000,
0≤Ai≤40000。

输入样例：4
6 2 9 1
输出样例：12

代码表示：

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int N=1e5+10;
int a[N];
int n;
int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
       { cin>>a[i] ;}
    sort(a,a+n);
    int mid=n/2;
    LL cnt=0;
    for(int i=0;i<n;i++)
    {
        cnt+=abs(a[i]-a[mid]);
    }
    cout<<cnt;
    return 0;
}

例付账问题

题目描述：

吃饭结帐的时候，常常会出现一些争执。现在有 n 个人出去吃饭，他们总共消费了 S 元。其中第 i 个人带了 ai 元。所有人带的钱的总数是足够付账的但每个人分别要出多少钱呢？为了公平起见，我们希望在总付钱量恰好为 S 的前提下，最后每个人付的钱的标准差最小。每个人支付的钱数可以是任意非负实数，即可以不是 11 分钱的整数倍。你需要输出最小的标准差是多少。

标准差的介绍：标准差是多个数与它们平均数差值的平方平均数，一般用于刻画这些数之间的“偏差有多大”。形式化地说，设第 i 个人付的钱为 bi 元，那么标准差为 :

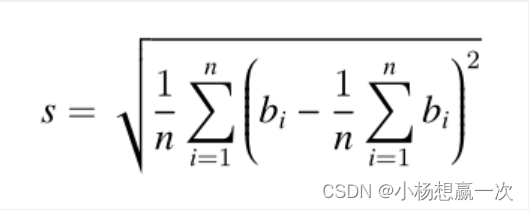
输入格式:

第一行包含两个整数 n、S；

第二行包含 n 个非负整数 a1, …, an。

输出格式：

输出最小的标准差，四舍五入保留 4 位小数。

数据范围：1≤n≤5×1e5；0≤ai≤1e9；0≤S≤1e15。

输入样例1：5 2333
666 666 666 666 666
输出样例1：0.0000
输入样例2：10 30
2 1 4 7 4 8 3 6 4 7
输出样例2：0.7928

思路：

在本题中x1+x2+x3+……+xn的值为0，也就是当x1、x2、x3……xn取到0为最小值。那么我们在求bi的时候就应该接近均值，我们才能求到方差的最小值

代码表示：

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int N=5e5+10;
 
int n;
long double s;
int a[N];
int main()
{
    cin>>n>>s;
//cur 表示当前人应该支付的金额，avg 表示每个人平均应该支付的金额。
    long double cur=0,avg=s/n,res=0;
    for(int i=0;i<n;i++)
    {
        scanf("%d",&a[i]);
    }
    sort(a,a+n);
    for(int i=0;i<n;i++)
    {
//cur 的计算公式为总支付金额 s 除以剩余人数 (n-i)
        cur=s/(n-i);//最小 
//确保每个人支付的金额不超过其所携带的钱数
        if(a[i]<cur)
            cur=a[i];
        res+=(cur-avg)*(cur-avg);
        s-=cur;
    }
    printf("%.4Lf",sqrt(res/n));
    return 0;
}

[蓝桥杯 2020 省 AB1] 解码

题目描述

小明有一串很长的英文字母，可能包含大写和小写。

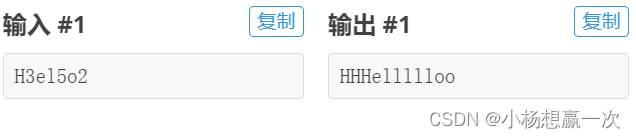
在这串字母中，有很多连续的是重复的。小明想了一个办法将这串字母表达得更短：将连续的几个相同字母写成字母 + 出现次数的形式。例如，连续的 5个 a，即 aaaaa，小明可以简写成 a5（也可能简写成 a4a、aa3a 等）。

对于这个例子：HHHellllloo，小明可以简写成 H3el5o2。为了方便表达，小明不会将连续的超过9个相同的字符写成简写的形式。

现在给出简写后的字符串，请帮助小明还原成原来的串。

输入格式

输入一行包含一个字符串。

输出格式

输出一个字符串，表示还原后的串。

思路提示：

1、对于每个大小写字母，如果下一个字符也为大小写字母，则代表这个字母只有一个，直接输出即可；如果下一个字符为数字 k，则输出 k 个这个字母。

2、条件判断 s[i] < '0' || s[i] > '9' 是用来判断字符串 s 中的字符 s[i] 是否为数字字符。

在ASCII字符集中，数字字符 '0' 到 '9' 的ASCII码连续递增。因此，通过比较字符 s[i] 的ASCII码与字符 '0' 和 '9' 的ASCII码的大小关系，可以确定字符 s[i] 是否为数字字符。

代码表示：

#include <bits/stdc++.h>
using namespace std;

string s;
int main() {
    cin >> s;
    for(int i = 0; i < s.size(); i++) {
        if(s[i] < '0' || s[i] > '9') {
            if(s[i + 1] < '0' || s[i + 1] > '9') {
                cout << s[i];
                continue;//跳过剩余的代码
            }
            //不符合上面的继续下面这部分代码 
            for(int j = 1; j <= s[i + 1] - '0'; j++) {
                cout << s[i];
            }
		}
    }
    return 0;
}

[蓝桥杯 2020 省 AB2] 成绩分析

题目描述

小蓝给学生们组织了一场考试，卷面总分为100 分，每个学生的得分都是一个 0 到 100 的整数。请计算这次考试的最高分、最低分和平均分。

输入格式：

输入的第一行包含一个整数 n，表示考试人数。

接下来 n 行，每行包含一个 0至100 的整数，表示一个学生的得分。

输出格式：

输出三行。

第一行包含一个整数，表示最高分。

第二行包含一个整数，表示最低分。

第三行包含一个实数，四舍五入保留正好两位小数，表示平均分。

代码表示：

第一种：有对应的函数

min_element 是 C++ 标准库算法中的一个函数，用于在给定范围内查找最小值。它不是一个特殊的函数，而是在 <algorithm> 头文件中定义的通用算法之一。

min_element 函数的原型如下：（*max_element基本上同理）

template <typename ForwardIt>
ForwardIt min_element(ForwardIt first, ForwardIt last);

该函数接受两个迭代器参数 first 和 last，表示要查找的范围。它返回一个指向范围中最小元素的迭代器。

使用 min_element 函数可以方便地找到给定范围内的最小值，而无需手动编写循环来逐个比较元素。

#include <bits/stdc++.h>
using namespace std;

int main() {
    int n;
    cin >> n;

    vector<int> scores(n);
    for (int i = 0; i < n; i++) {
        cin >> scores[i];
    }

    int minScore = *min_element(scores.begin(), scores.end());
    int maxScore = *max_element(scores.begin(), scores.end());
    double averageScore = round(accumulate(scores.begin(), scores.end(), 0) / static_cast<double>(n) * 100) / 100.0;

    cout << maxScore << endl;
    cout << minScore << endl;
    cout << averageScore << endl;

    return 0;
}

第二种：这种要注意我们需要事先初始化一个最大值和一个最小值！一开始我写的两个来回倒就搞混了。

#include <bits/stdc++.h>
using namespace std;

int main() {
    int n;
    cin >> n;

    int minScore = INT_MAX;  // 初始化为最大整数
    int maxScore = INT_MIN;  // 初始化为最小整数
    int sum = 0;                                 // 分数总和

    int arr[10001];
    for (int i = 0; i < n; ++i) {
        cin >> arr[i];
        int score = arr[i];

        // 更新最低分和最高分
        if (score < minScore) {
            minScore = score;
        }
        if (score > maxScore) {
            maxScore = score;
        }

        sum += score;  // 累加分数
    }

    double averageScore = static_cast<double>(sum) / n;  // 计算平均分

    cout << maxScore << endl;
    cout << minScore << endl;
    cout << fixed << setprecision(2);  // 设置输出保留两位小数
    cout << averageScore << endl;

    return 0;
}

注意：

setprecision(2) 用于设置输出流的精度，指定小数部分的位数为2位。这意味着输出流将在小数点后显示两位数字。写在需要的数字前面即可。

如果我使用printf来表示的话： %.nf 来表示保留 n 位小数，其中 n 是一个非负整数。例如，%.2f 表示保留两位小数。