本专栏为大家分享本人学习算法遇到的不同类型的题目以及解析!''
此篇文章给大家分享一些关于位运算算法的题目,在开篇还讲述了常见位运算的公式以及题目,如果对您有帮助,麻烦点个关注,如有错误,请您指出!
1.常见位运算总结(包含5道题目)
1.1基础位运算
| 运算符 | 操作 |
|---|---|
| << | 左移 |
| >> | 右移 |
| ~ | 取反 |
| & | 对应二进制位有0就是0 |
| | | 对应二进制位有1就是1 |
| ^ | 对应二进制位,相同为0相异为1 / 不进位相加 |
对于^运算的不进位相加解释:假设为
0 1 0
0 1 1
那么不进位相加就是 0 0 1,这个理解在我们后面是有用的
1.2给一个数n,确定他的二进制位中的第x为是0还是1
利用&(对应二进制位有0就是0)运算即可,将 n >> x后,他的第x为就在最右边,那么此时& 一个1,那么就只会得到1 或 0,如果是1,那么这个位上是1,反之则是0
即 (n>> x) &1
1.3将一个数n的二进制表示的第x位修改为1
方法: n | (1 << x) 即可:
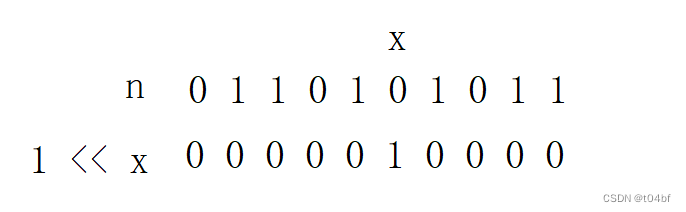
这样,能保证其他位的不变,将对应x位改为1
1.4将一个数n的二进制表示的第x位修改为0
方法: 要想将某一位修改为0,那么就让这一位 & 0即可,但是怎么得到仅是这一位为0的数字呢??
我们将1 << x后取反即可
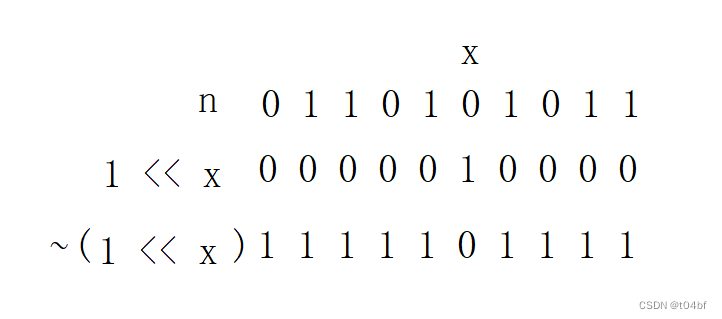
这样,通过 n & (~(1 << x))就能得到所求
1.5位图的思想
哈希表实际上大多数情况下是个数组,通过数组的内容来存储数据
实际上二进制位同样有这个效果:
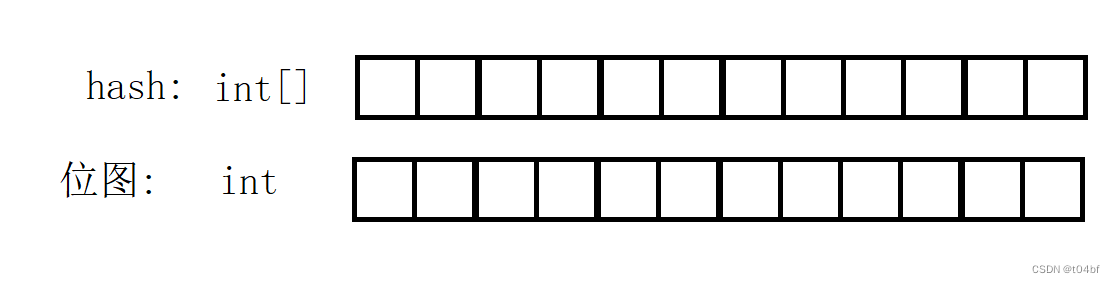
通过二进制位上是0还是1来存储信息,而我们上面的1.2 ~ 1.4的方法主要是为了以后操作位图做好准备
1.6提取一个数n二进制表示中最右侧的1
方法: n & -n
-n操作实际上就是将原数取反后 +1 的操作,
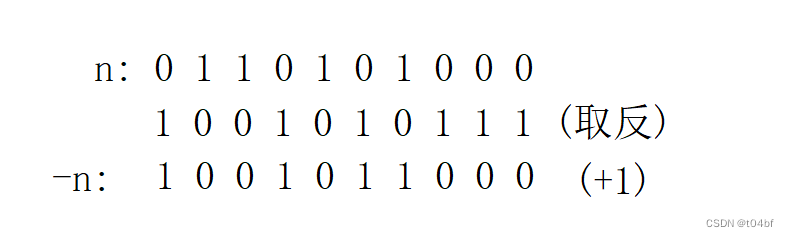
这样我们会发现,n与-n相比,原数最右侧的1的左边变成原来相反,右侧则不变,还是0
那么我们将 n & -n后,就能提取出最右侧的1
1.7去掉一个数n二进制表示中最右侧的1
方法: n & (n-1)
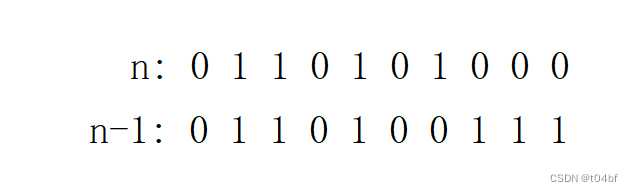
实际上n-1的操作就是从右往左进行借位的操作,因为在遇到最右侧的1之前,其余位都是0,是不够-1的,那么就要借位,直到遇见1
那么n-1后就得到与原来的n相比:最右侧的1(包括这个1)的右侧都是原来的相反数,而左侧的不变
那么我们将n & n-1后,就能将原数最右侧的1去掉
这种类型的题目:
(1)位1的个数. - 力扣(LeetCode)
题解:
public int hammingWeight(int n) {
int count = 0;
while(n != 0){
n &= n-1;
count++;
}
return count;
}
}
(2)比特位计数. - 力扣(LeetCode)
题解:
class Solution {
public int[] countBits(int n) {
int[] ret = new int[n+1];
for(int i = 0; i <= n; i++){
int tmp = i;
while(tmp != 0){
tmp &= (tmp-1);
ret[i]++;
}
}
return ret;
}
}(3)汉明距离:. - 力扣(LeetCode)
题解:
class Solution {
public int hammingDistance(int x, int y) {
x = x ^ y;
int count = 0;
while(x != 0){
x &= (x-1);
count++;
}
return count;
}
}1.8异或运算的运算律
实际上我们用前面讲到的不进位相加就能理解
(1)a ^ 0 = a

(2)a ^ a = 0(形象称为消消乐)

(3)a ^ b ^ c = a ^ (b ^ c)
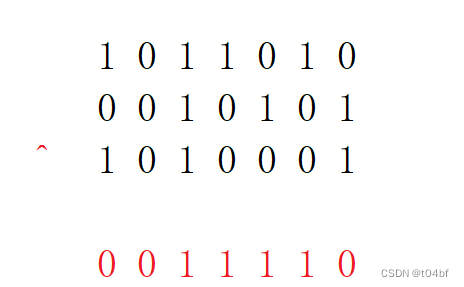
那么不进位相加实际上就是每一列抵消1的过程,既然这样,那就和顺序毫无关系了,因此满足交换律
这种类型的题目:
(1)只出现一次的个数:. - 力扣(LeetCode)
题解:
class Solution {
public int singleNumber(int[] nums) {
int ret = 0;
for(int x : nums){
ret ^= x;
}
return ret;
}
}(2)只出现一次的数字 III:
题目:. - 力扣(LeetCode)
解析:如果将给定数组里面的所有数都异或起来,那么最后得到的数一定是一个非0的数,因为如果为0那么这两个只出现一次数就相等了.我们将这两个数字记作m,n,数组全部异或后得到x.
如果我们提取出x的二进制表示中最低位的1,假设是第k位.那么根据异或操作等效于不进位相加,m n的第k位一定只有一个是1,另一个第k位一定是0;而在数组中,除了这两个数以外,其他数都是成对出现的,数组里面的任何数也可以分成两派,一派第k位是1,另一派第k位是0;如果我们能把数组里面的元素按照这两派分开,那么m,n一定是在不同的派,由于其他数都是成对出现的,那么分别将两派里面的元素全部异或,就能得到m和n
那么接下来的重点就在于如何分派,我们前面已经提取出x的最低位的1,这里设为tmp,可以利用tmp进行分派,如果一个数的第k位是0,那么这个数 & tmp结果就是0;反之则是1,这样就能分派了
最后,还有一个细节问题,我们前面说过提取最低位的1方法是 n & (n-1),但是如果n刚好是int类型的最小值,即二进制:10000000,00000000,00000000,00000000,因为这个数进行-n操作后还是他本身,所以我们就不能提取出最后一个n,而恰恰这个数提取出最低位的1后就是他本身,那么就不用提取了
题解:
class Solution {
public int[] singleNumber(int[] nums) {
int x = 0;
for(int t : nums){
x ^= t;
}
int tmp = (x == Integer.MIN_VALUE ? x : x & (-x));
int type1 = 0;
int type2 = 0;
for(int t : nums){
if((t & tmp)== 0){
type1 ^= t;
}else{
type2 ^= t;
}
}
return new int[]{type1,type2};
}
}2.丢弃的数字
题目:. - 力扣(LeetCode)
2.1解析
此题就是在一段连续区间内找到缺失的那一个数.假设给定的数组长度是x,由于数组是缺少了一个数,那么完全的区间应该是0<= x <= n.
对于此类问题我们利用哈希表当然是做得出来,但是这类题利用位运算的方法更加巧妙
我们前面说过,两个相同的数进行异或操作得到的是0
我们前也做过一道题:只出现一次的数字,即在数组中,除了一个数只出现了一次,其余数字都出现了两次,我们将这个数组元素全部异或起来就能得到这个只出现一次的数
在这道题:如果我们将原数组 和 完全的区间结合起来形成一个新的数组,那问题不就转化为只出现一次的数字的问题了吗,因为在新数组中,除了确失的那个数以外,其余数都出现了两次.
2.2题解
class Solution {
public int missingNumber(int[] nums) {
int ret = 0;
int n = nums.length;
for(int i = 0; i < n+1; i++){
ret ^= i;
}
for(int x : nums){
ret ^= x;
}
return ret;
}
}3.两整数之和
题目:. - 力扣(LeetCode)
3.1解析
在做这道题之前,有一个重要的前提知识(我在做这道题之前实际上是不知道的):
两个整数相加,实际上对应的二进制相加的结果就是两个整数相加的结果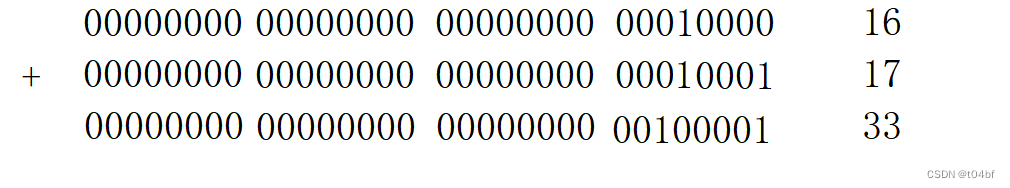
既然题目要求不能用+和-,那么我们就利用位运算来计算,那么二进制的加法实际上也分成两个步骤:相加 和 进位
(1)对应位置相加
我们前面说过异或运算实际上就是不进位相加,这不就是正好满足我们的要求吗
那么我们就可以先把要相加的两个数进行异或,得到的就是未进位的和
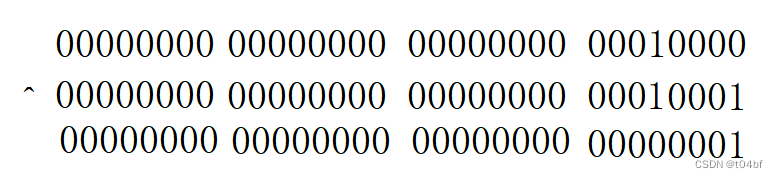
(2)进位操作
实际上进位操作无非就是两个1相加那就进1,那么我们的&运算不正好满足对应二进制位两个为1才为1吗,只不过&运算的结果是在原位置,但是无妨,我们将得到的结果 << 1位即可
最后将(1)的得到的数 与 (2)得到的数 再次进行^操作,此时还可能会有进位,因此这个操作我们要循环进行,直到(2)操作得到的数字为0,说明相加结果没有进位了,那么循环结束
那么这样的话,我们就用二进制的位运算来代替了原来的加减法
3.2题解
class Solution {
public int getSum(int a, int b) {
int m = a ^ b;
int n = (a & b) << 1;
while(n != 0){
int tmp = m ^ n;
n = (m & n) << 1;
m = tmp;
}
return m;
}
}4.只出现一次的数字II
题目:. - 力扣(LeetCode)
4.1解析

假设题目给我们的是如图所示的数组,只有一个元素出现了1次,其他的都出现了3次.我们将数组元素十进制转化为二进制,就会发现,如果我们将所有元素的某一个二进制位加起来,得到的结果去%3,得到的就一定是[只出现一次]的那个数的对应比特位.比如:我们将所有元素的第0比特位相加,那么就会得到4,4 % 3 = 1,那么99的第0位比特位就是0
4.2题解
class Solution {
public int singleNumber(int[] nums) {
int ret = 0;
for(int i = 0; i < 32; i++){
int sum = 0;
for(int x : nums){
sum += (x >> i) & 1;
}
sum %= 3;
if(sum == 1){
ret |= (1 << i);
}
}
return ret;
}
}5.消失的两个数字
题目:. - 力扣(LeetCode)
5.1解析
实际上这道题实际上就是(丢失的数字)和(只出现一次的数字 III)
如果给定数组的长度是n,那么完全的数据范围就是 1 <= x <= n+2.在(只出现一次的数字 III)中,数组元素中,有两个出现了一次,其余都出现了两次;那么在这道题中,我们就可以利用(丢失的数字)的思想来将这道题转化为(只出现一次的数字 III)的题目,即把我们完全的数字范围与 给定的数组合成一个新数组.假设我们的数组是:[2,3],那么数据范围就是1,2,3,4,那么新的数组就是:1,2,2,3,3,4.在这个数组中利用(只出现一次的数字 III)的思想来解决这道题
5.2题解
class Solution {
public int[] missingTwo(int[] nums) {
int k = 0;
int n = nums.length;
for(int i = 1; i <= n+2; i++){
k ^= i;
}
for(int x : nums){
k ^= x;
}
k = (k == Integer.MIN_VALUE ? k : k & (-k));
int type1 = 0,type2 = 0;
for(int i = 1; i <= n+2; i++){
if((k & i) == 0){
type1 ^= i;
}else{
type2 ^= i;
}
}
for(int x : nums){
if((k & x) == 0){
type1 ^= x;
}else{
type2 ^= x;
}
}
return new int[]{type1,type2};
}
}