1.是什么
- 沿着一条路径一直搜索下去,在无法搜索时,回退到刚刚访问过的节点。
- 并且每个节点只能访问一次。
- 本质上是持续搜索,遍历了所有可能的情况,必然能得到解。
- 流程是一个树的形式,每次一条路走到黑。
- 目的主要是达到被搜索结构的叶结点直到最后一层,然后回退到上层,被 访问过的节点会被标记,然后查看是否有其他节点,如果有则继续下一层 ,直到最后一层。一次类推直到所有节点都被查找。
- 后访问的节点,其邻接点先被访问。
- 根据深度优先遍历的定义,后来的先搜索(栈、递归)(先进后出)。
- 初始化图中的所有节点为均未被访问。
- 从图中的某个节点v出发,访问v并标记其已被访问。
- 依次检查v的所有邻接点w,如果w未被访问,则从w出发进行
- 深度优先遍历(递归调用,重复步骤(2)和(3))。
2.学习案例
2.1问题
2.2求解思路
每一个坐标都有上下左右四个方向可以走,如果不是障碍物那么可以视作有效的步数,一直往前走的过程中要注意标记已经访问过后的坐标,在回溯的时候也要注意将坐标清除标记。
2.3代码实现
start_x, start_y, end_x, end_y = map(int, input().split()) maps = [] for i in range(5): l = list(map(int,input().split())) maps.append(l) min = 9999999 vis = [[0 for _ in range(4)] for _ in range(5)] def dfs(x,y,step): global min, vis d = [(0,1),(1,0), (0,-1),(-1,0) ] if x == end_x-1 and y == end_y-1: if step<min: min = step return for xx, yy in d: dx = x+xx dy = y+yy if 0 <= dx < 5 and 0 <= dy < 4: if maps[dx][dy] == 0 and vis[dx][dy] == 0: vis[dx][dy] = 1 dfs(dx, dy, step + 1) vis[dx][dy] = 0 return dfs(start_x-1,start_y-1,0) print(min)输入:
1 1 4 3 0 0 1 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1输出:
7
3.刷题笔记
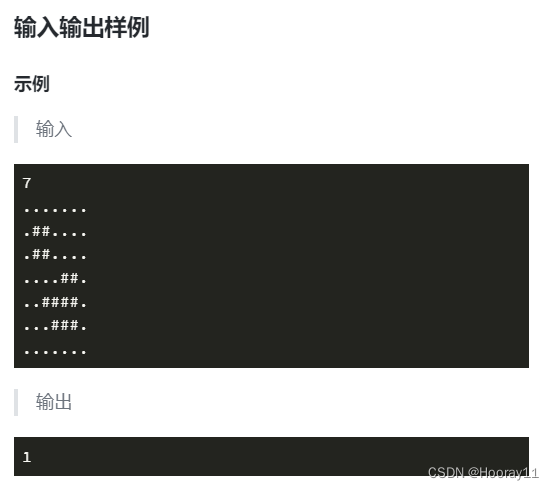
3.1全球变暖
6.全球变暖 - 蓝桥云课 (lanqiao.cn)
求解思路 :
与其说他是一道深搜的题,我觉得更应该归类为栈模拟的题目,在搜索的过程中主要是栈模拟从而实现深度优先搜索。
这道题是要求求出有多少岛屿会被淹没,换个思路来想的话什么样的岛屿会被淹没,什么样的岛屿不会被淹没。题目中这一个条件很关键(岛屿边缘一个像素的范围会被海水淹没。具体来说如果一块陆地像素与海洋相邻(上下左右四个相邻像素中有海洋),它就会被淹没。)所以我们就可以总结出如果岛屿中存在一块上下左右四个方向一个像素的距离都是陆地的一个岛屿,那么这一块不会被淹没,我们可以把它当作一个高地。
而所谓的岛屿就是周围是海洋,由陆地联通起来的区域,所以在计算时需要建立一个访问标记数组用来做标记。
n = int(input())
maps = []
for i in range(n):
l = list(input())
maps.append(l)
vis = [[0]*n for _ in range(n)]
d = [(1,0),(-1,0),(0,1),(0,-1)]
def dfs(x,y):
stack = [(x,y)]
noHigh = True
while stack:
tx, ty = stack.pop()
if maps[tx - 1][ty] == '#' and maps[tx + 1][ty] == '#' and maps[tx][ty + 1] == '#' and maps[tx][ty - 1] == '#':
noHigh = False
for xx, yy in d:
dx = tx + xx
dy = ty + yy
if maps[dx][dy] == '#' and vis[dx][dy] == 0:
vis[dx][dy] = 1
stack.append((dx,dy))
return noHigh
ans = 0
for i in range(1,n-1):
for j in range(1,n-1):
if maps[i][j] == '#' and vis[i][j] == 0:
if dfs(i,j):
ans += 1
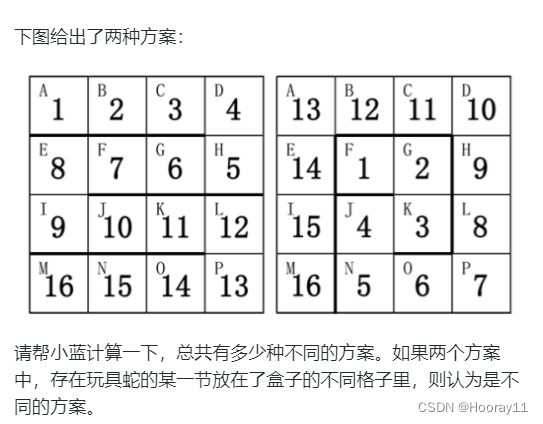
print(ans)3.2玩具蛇
0玩具蛇 - 蓝桥云课 (lanqiao.cn)
求解思路
这道题有点像1到16这些数字的全排列。如果16个数字的排完之后就可以认为是一种方案,而排完一个的下一个的位置可以选择四种(上下左右),这就会体现深度优先搜索,一条路走到黑然后再慢慢的回溯。
而我们传入的值是什么,是第一个数字的位置以及现在已经有多少个数字完成了排列。
d = [(1,0),(-1,0),(0,1),(0,-1)]
ans = 0
vis = [[0]*4 for _ in range(4)]
def dfs(x,y,count):
global ans
if count == 16:
ans += 1
return
for xx, yy in d:
dx = x+xx
dy = y+yy
if 0<=dx<4 and 0<=dy<4 and vis[dx][dy] == 0 :
vis[dx][dy] = 1
dfs(dx,dy,count+1)
vis[dx][dy] = 0
for i in range(4):
for j in range(4):
vis[i][j] = 1
dfs(i,j,1)
vis[i][j] = 0
print(ans)3.3最大连通
7.最大连通 - 蓝桥云课 (lanqiao.cn)
求解思路:
做到这道题的时候我突然对深搜有了一点点的想法,仔细观察了之前两道题得到代码,我们 可以知道一个用栈进行了存储,而有一个是非常典型的深搜在一条路上走到黑。至于根本的区别我还没想到可能需要做更多的题目才能总结出来的。
做这道题的时候,我一开始用的是典型的深搜在一条路上走到黑,但是不行,我也不知道是为什么,然后就换了栈模拟的这种,然后就可以。还不知道是为什么,,,,
flag = [[0]*60 for _ in range(30)]
maps =[
"110010000011111110101001001001101010111011011011101001111110",
"010000000001010001101100000010010110001111100010101100011110",
"001011101000100011111111111010000010010101010111001000010100",
"101100001101011101101011011001000110111111010000000110110000",
"010101100100010000111000100111100110001110111101010011001011",
"010011011010011110111101111001001001010111110001101000100011",
"101001011000110100001101011000000110110110100100110111101011",
"101111000000101000111001100010110000100110001001000101011001",
"001110111010001011110000001111100001010101001110011010101110",
"001010101000110001011111001010111111100110000011011111101010",
"011111100011001110100101001011110011000101011000100111001011",
"011010001101011110011011111010111110010100101000110111010110",
"001110000111100100101110001011101010001100010111110111011011",
"111100001000001100010110101100111001001111100100110000001101",
"001110010000000111011110000011000010101000111000000110101101",
"100100011101011111001101001010011111110010111101000010000111",
"110010100110101100001101111101010011000110101100000110001010",
"110101101100001110000100010001001010100010110100100001000011",
"100100000100001101010101001101000101101000000101111110001010",
"101101011010101000111110110000110100000010011111111100110010",
"101111000100000100011000010001011111001010010001010110001010",
"001010001110101010000100010011101001010101101101010111100101",
"001111110000101100010111111100000100101010000001011101100001",
"101011110010000010010110000100001010011111100011011000110010",
"011110010100011101100101111101000001011100001011010001110011",
"000101000101000010010010110111000010101111001101100110011100",
"100011100110011111000110011001111100001110110111001001000111",
"111011000110001000110111011001011110010010010110101000011111",
"011110011110110110011011001011010000100100101010110000010011",
"010011110011100101010101111010001001001111101111101110011101"]
d = [(1,0),(-1,0),(0,1),(0,-1)]
def dfs(x,y):
stack = [(x,y)]
count = 0
while stack:
tx, ty = stack.pop()
for xx,yy in d:
dx = tx+xx
dy = ty+yy
if 0<=dx<30 and 0<=dy<60:
if maps[dx][dy] == '1' and flag[dx][dy] == 0:
flag[dx][dy] = 1
count += 1
stack.append((dx,dy))
return count
max = 0
for i in range(30):
for j in range(60):
if maps[i][j] == '1' and flag[i][j] == 0:
count = dfs(i,j)
if count>max:
max = count
print(max)