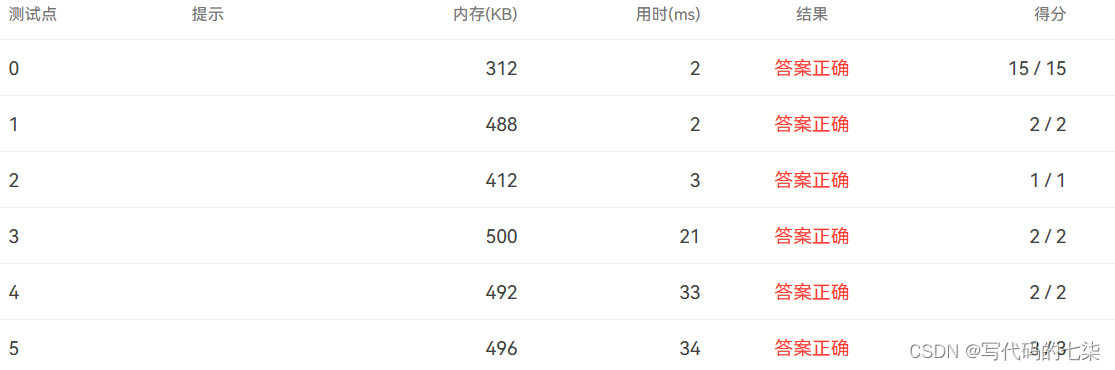
题目描述:
有一根长度为 len 的横向的管道,该管道按照单位长度分为 len 段,每一段的中央有一个可开关的阀门和一个检测水流的传感器。
一开始管道是空的,位于 Li的阀门会在 Si 时刻打开,并不断让水流入管道。
对于位于 Li的阀门,它流入的水在 Ti(Ti≥Si)时刻会使得从第 Li−(Ti−Si) 段到第 Li+(Ti−Si)段的传感器检测到水流。
求管道中每一段中间的传感器都检测到有水流的最早时间。
输入格式:
输入的第一行包含两个整数 n,len,用一个空格分隔,分别表示会打开的阀门数和管道长度。
接下来 n行每行包含两个整数 Li,Si,用一个空格分隔,表示位于第 Li 段管道中央的阀门会在 Si 时刻打开。
输出格式:
输出一行包含一个整数表示答案。
数据范围:
对于 30%的评测用例,n≤200,Si,len≤3000;
对于 70%的评测用例,n≤5000,Si,len≤1e5;
对于所有评测用例,1≤n≤1e5,1≤Si,len≤1e9,1≤Li≤len,Li−1<Li。
输入样例:
3 10
1 1
6 5
10 2
输出样例:
5分析步骤:
第一:我们拿到这道题我们可以看到,是一段管道里有许多的水龙头,当开启不同水龙头的时候它可以向两边扩散速度是:1段/s。不同水龙头控制的区域也不一样,至此我们分析出了第一个特点有区间问题,需要合并看看有没有全部覆盖管道;
我们还可以发现当时间开的越长,管道内有水的区域也越长,这呈现一种单调的特点,并且我们可以求出一个时间点,在这个时间点的左边管道内不能全部都流过水,在这个时间点和以后都可以覆盖全管道。至此也满足了二分的特点;
所以本题要运用二分+区间合并来做;
第二:知道了考的知识点,咱们就要书写主函数,把握整体框架。
首先把值都输入进去,其次开始二分
定义我们的左节点 l 为 0 因为有可能水管从第零分钟就一直开着,并且每个管道段落都有水龙头,所以最小时间可能是 0 ;
定义右节点 r 为 2e9 .因为题目说了 Si 最大为 1e9 所以有可能在最后一秒也就是1e9秒时 ,开启开关并且只有一个开关且在第一个管道之内,所以要覆盖管道又要1e9s 所以两个 1e9 相加就是 2e9。
求出mid,再判断一下这个 mid 的值
如果是对的,则证明比 mid 的时间大小更大的值就更可以覆盖满管道.因为假如 mid 为5秒时已经覆盖了管道,那么6秒更会是管道内充水。所以应该将 mid 赋值给 r
如果 mid 的时间大小不可以,那么比mid还小的话更是不可能覆盖的了管道了。所以应该将 mid + 1 的值 赋值给 l;
int main()
{
cin>>n>>m;
for(int i = 0 ; i < n ; i ++){
cin>>q[i].x>>q[i].y;
}
LL l = 0 , r = 2e9;
while(l<r){
LL mid = (l+r) / 2;
if(check(mid)) r = mid;
else l = mid + 1;
}
cout<<r;
return 0;
}第三:书写 check 函数定义一个 计数器 cnt 用一个f or 循环将之前存储的数据取出来,如果mid这个时间大于了我们的S这个时间的话,那么就意味着这个开关已经开启了并且流出了一段的水,这段时间的差值 就是这个开关向左右两边扩散的距离,所以我们用 t 计算出这段时间差。
确定左右区间:
我们接下来看这个开关可以控制的区间范围因为 t 就是扩散的距离 所以我们的 int l = max(1, L-t ) ,左边界范围就是第 L 个开关向左走了 t 时间的路 和 1 取最大值进行动态更新
r = min((LL)m,(LL)L+t);右边界范围就是第 L 个开关向左走了 t 时间的路 和 m 取最小值进行动态更新因为不可以超过管道长度。
最后将这个开关的区间边界放入 p 数组之中;至此我们区间范围已然确定。
int cnt = 0 ;
for(int i = 0 ; i < n ; i ++){
int L = q[i].x , S = q[i].y;
if(mid >= S){
int t = mid - S;
int l = max(1,L-t) , r = min((LL)m,(LL)L+t);
p[cnt++]={l,r};
}
}第四:接下来进行区间合并。我们先进行sort排序这样这些区间的左端点就可以从小到大排序,我们就只要比较右端点就行。
我们定义左端点 st 为 -1 ; 右端点ed 为 -1
如果 我们的左端点st <= 上一个存值的区间右端点 加 1 的话我们就只需要更新一下我们右节点 ed 就可以把两个区间合并了。为什么要加1?直接小于等于 ed 不行吗? 不可以 。因为ed那里已经有水了,只是 ed+1 的那个点没有水,所以如果我们的 l == ed+1的话也是可以算连接上了的。
如果 我们的左端点st > 上一个存值的区间右端点 加 1 的话 就证明这两个区间必有间隙则更改我们的st 和 ed为新的区间端点。
最终返回判断一下st是否为 1 并且 ed是否为管道长度。如果都符合就返回true,有一个不符合就是false;
sort(p,p+cnt);
int ed = -1 , st = -1;
for(int i = 0 ; i < cnt ; i ++){
if(p[i].x <= ed + 1 ) ed = max(ed , p[i].y);
else st = p[i].x , ed = p[i].y;
}
return st == 1 and ed == m;
注意:区间合并就三种情况相交里包含两种,还有一种相离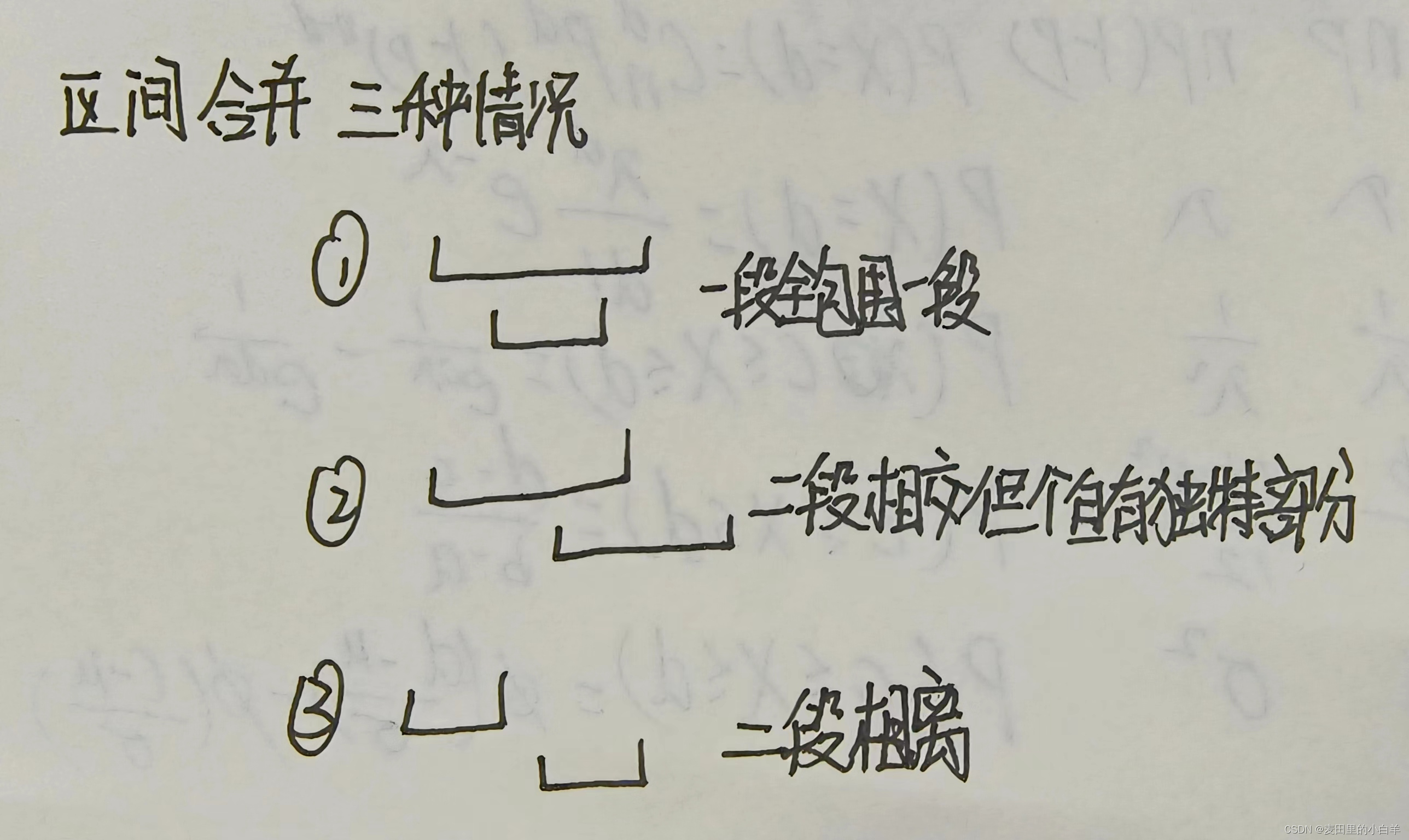
代码:
#include <iostream>
#include <cstring>
#include <algorithm>
#define x first
#define y second
using namespace std;
const int N = 1e5+10;
typedef long long LL;
typedef pair<int, int> PII;
PII q[N], p[N];
LL n,m;
bool check(int mid){
int cnt = 0 ;
for(int i = 0 ; i < n ; i ++){
int L = q[i].x , S = q[i].y;
if(mid >= S){
int t = mid - S;
int l = max(1,L-t) , r = min((LL)m,(LL)L+t);
p[cnt++]={l,r};
}
}
sort(p,p+cnt);
int ed = -1 , st = -1;
for(int i = 0 ; i < cnt ; i ++){
if(p[i].x <= ed + 1 ) ed = max(ed , p[i].y);
else st = p[i].x , ed = p[i].y;
}
return st == 1 and ed == m;
}
int main()
{
cin>>n>>m;
for(int i = 0 ; i < n ; i ++){
cin>>q[i].x>>q[i].y;
}
LL l = 0 , r = 2e9;
while(l<r){
LL mid = (l+r) / 2;
if(check(mid)) r = mid;
else l = mid + 1;
}
cout<<r;
return 0;
}