备战2024年蓝桥杯 -- 每日一题
Python大学A组
试题一:木棒
试题二:n皇后问题
试题三:糖果
试题四:飞机降落
试题五:生日蛋糕
试题一:木棒
【问题描述】
乔治拿来一组等长的木棒,将它们随机地砍断,使得每一节木棍的长度都不超过 5050 个长度单位。然后他又想把这些木棍恢复到为裁截前的状态,但忘记了初始时有多少木棒以及木棒的初始长度。请你设计一个程序,帮助乔治计算木棒的可能最小长度。每一节木棍的长度都用大于零的整数表示。
【输入格式】
输入包含多组数据,每组数据包括两行。
第一行是一个不超过 6464 的整数,表示砍断之后共有多少节木棍。
第二行是截断以后,所得到的各节木棍的长度。
在最后一组数据之后,是一个零。
【输出格式】
为每组数据,分别输出原始木棒的可能最小长度,每组数据占一行。
【数据范围】
数据保证每一节木棍的长度均不大于 5050。
【输入样例】
9
5 2 1 5 2 1 5 2 1
4
1 2 3 4
0【输出样例】
6
5【解题思路】

【Python程序代码】
x = int(input())
def dfs(u,now,start):
if u*l==suma:return True
if now==l:return dfs(u+1,0,0)
i = start
while i<x:
if st[i]:i+=1; continue
if a[i]+now>l:i+=1; continue
st[i]=True
if dfs(u,now+a[i],i+1):return True
st[i]=False
if start==0 or now+a[i]==l:return False
j = i
while j<x and a[j]==a[i]:j+=1
i = j-1
i += 1
return False
while x:
a = list(map(int,input().split()))
suma = sum(a)
st = [0]*(70)
a.sort(reverse=True)
for i in range(len(a)):
if a[i]>50:st[i]=1
l = 1
while 1:
if suma%l==0 and dfs(0,0,0):
print(l); break
l += 1
x = int(input())试题二: n-皇后问题
【问题描述】
n−皇后问题是指将 n个皇后放在 n×n 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
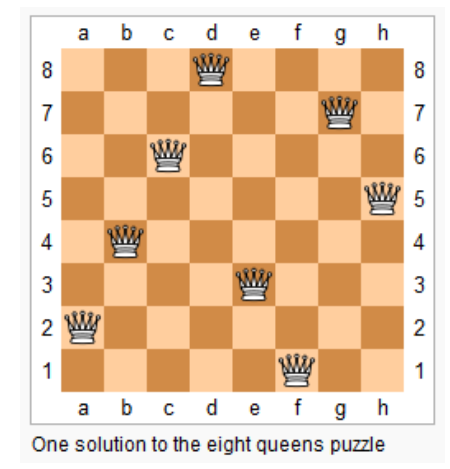
现在给定整数 n,请你输出所有的满足条件的棋子摆法。
【输入格式】
共一行,包含整数 n。
【输出格式】
每个解决方案占 n 行,每行输出一个长度为 n 的字符串,用来表示完整的棋盘状态。
其中 . 表示某一个位置的方格状态为空,Q 表示某一个位置的方格上摆着皇后。
每个方案输出完成后,输出一个空行。
【数据范围】
1≤n≤9
【输入样例】
4【输出样例】
.Q..
...Q
Q...
..Q.
..Q.
Q...
...Q
.Q..【解题思路】
经典DFS问题,必做题,直接见代码
【Python程序代码】
n = int(input())
r,l,dg,udg = [0]*(n+5),[0]*(n+5),[0]*(2*n+5),[0]*(2*n+5)
st = [[0]*(n+5) for _ in range(n+5)]
def dfs(u):
if u==n+1:
for i in range(1,n+1):
for j in range(1,n+1):
if st[i][j]:print('Q',end='')
else:print('.',end='')
print()
print()
for i in range(1,n+1):
if r[i] or l[u] or dg[i-u+n] or udg[i+u]:continue
st[i][u]=1
r[i]=l[u]=dg[i-u+n]=udg[i+u]=1
dfs(u+1)
st[i][u]=0
r[i] = l[u] = dg[i - u + n] = udg[i + u] = 0
dfs(1)试题三:糖果
【题目描述】
糖果店的老板一共有 M 种口味的糖果出售。为了方便描述,我们将 M 种口味编号 1∼M。小明希望能品尝到所有口味的糖果。遗憾的是老板并不单独出售糖果,而是 K颗一包整包出售。幸好糖果包装上注明了其中 K 颗糖果的口味,所以小明可以在买之前就知道每包内的糖果口味。给定 N 包糖果,请你计算小明最少买几包,就可以品尝到所有口味的糖果。
【输入格式】
第一行包含三个整数 N,M,K。
接下来 N 行每行 K 个整数 T1,T2,⋅⋅⋅,TK,代表一包糖果的口味。
【输出格式】
一个整数表示答案。
如果小明无法品尝所有口味,输出 −1。
【数据范围】
1≤N≤100,
1≤M,K≤20,
1≤Ti≤M
【输入样例】
6 5 3
1 1 2
1 2 3
1 1 3
2 3 5
5 4 2
5 1 2【输出样例】
2【解题思路】
可重复覆盖问题,搜索顺序:依次枚举品尝每种糖果(每一列)到底选哪一包糖果(哪一行),看看哪一行有该种类糖果(该列为1表示有该种类糖果)直到把所有的列都覆盖完为止,或者发现有一列无法覆盖也结束,说明无解。
优化方法:
1.迭代加深:枚举答案,看看答案是1包能不能覆盖所有类糖,答案是2包能不能覆盖所有类糖…
2.从少分支的开始枚举
3.可行性剪枝:添加估价函数h(),至少要选多少行?如果当前剩下的行数<最少的行数,那么肯定无法覆盖。h()的计算:如果某一列没选,就把这一列所有能选的行数都选掉,算作选了1行,这样算出来的行数肯定是<=正确结果的最小行数的。
4.位运算优化
【Python程序代码】
n,m,k = map(int,input().split())
l2,col = [0]*(1<<m+1),[[] for _ in range(m+5)]
def lowbit(x):
return x&-x
def h(state):
res = 0
i = (1<<m)-1-state
while i:
c = l2[ lowbit(i) ]
for r in col[c]:
i&=~r
res += 1
i -= lowbit(i)
return res
def dfs(res,state):
if res==0 or h(state)>res:return state==(1<<m)-1
t = -1
i = (1<<m)-1-state
while i:
c = l2[ lowbit(i) ]
if t==-1 or len(col[t])>len(col[c]):
t = c
i -= lowbit(i)
for r in col[t]:
if dfs(res-1,state|r):return True
return False
for i in range(m):l2[1<<i]=i
for i in range(n):
tep = list(map(int,input().split()))
state = 0
for j in range(k):
c = tep[j]
state |= 1<<(c-1)
for j in range(m):
if state&(1<<j):col[j].append(state)
res = 1
tep = [[] for _ in range(m+5)]
for i in range(m):
tp = set(col[i])
tep[i]+=list(tp)
col = tep
while res<=m and dfs(res,0)==False:res+=1
if res>m:res=-1
print(res)
试题四:飞机降落
【题目描述】
有 N 架飞机准备降落到某个只有一条跑道的机场。其中第 i架飞机在 Ti 时刻到达机场上空,到达时它的剩余油料还可以继续盘旋 Di 个单位时间,即它最早可以于 Ti 时刻开始降落,最晚可以于 Ti+Di 时刻开始降落。降落过程需要 Li 个单位时间。一架飞机降落完毕时,另一架飞机可以立即在同一时刻开始降落,但是不能在前一架飞机完成降落前开始降落。请你判断 N 架飞机是否可以全部安全降落。
【输入格式】
输入包含多组数据。
第一行包含一个整数 T,代表测试数据的组数。
对于每组数据,第一行包含一个整数 N。
以下 N 行,每行包含三个整数:Ti,Di 和 Li
【输出格式】
对于每组数据,输出 YES 或者 NO,代表是否可以全部安全降落。
【数据范围】
对于 30% 的数据,N≤2。
对于 100%的数据,1≤T≤10,1≤N≤10,0≤Ti,Di,Li≤100000。
【输入样例】
2
3
0 100 10
10 10 10
0 2 20
3
0 10 20
10 10 20
20 10 20【输出样例】
YES
NO【解题思路】
简单的DFS,考虑所有的排列情况然后判定是否可以全部降落即可。也可以直接进行DFS。
【Python程序代码】
t = int(input())
def dfs(start,u):
global flag
if u==n:
flag = 1
return
if flag==1:return
for i in range(n):
if st[i]:continue
t,d,l = tdl[i]
if t+d>=start:
st[i] = 1
dfs(max(start,t)+l,u+1)
st[i] = 0
else:continue
for _ in range(t):
n = int(input())
tdl = []
st = [0]*(20)
for i in range(n):
tdl.append(list(map(int,input().split())))
flag = 0
dfs(0,0)
if flag:print('YES')
else:print('NO')试题五:生日蛋糕
【问题描述】
7 月 17日是 Mr.W 的生日,ACM-THU 为此要制作一个体积为 Nπ 的 M层生日蛋糕,每层都是一个圆柱体。设从下往上数第 i 层蛋糕是半径为 Ri,高度为 Hi的圆柱。当 i<M时,要求 Ri>Ri+1 且 Hi>Hi+1。由于要在蛋糕上抹奶油,为尽可能节约经费,我们希望蛋糕外表面(最下一层的下底面除外)的面积 Q 最小。令 Q=Sπ,请编程对给出的 N 和 M,找出蛋糕的制作方案(适当的 Ri 和 Hi的值),使 S 最小。除 Q 外,以上所有数据皆为正整数。
【输入格式】
输入包含两行,第一行为整数 N,表示待制作的蛋糕的体积为 Nπ。
第二行为整数 M,表示蛋糕的层数为 M。
【输出格式】
输出仅一行,是一个正整数 S(若无解则 S=0)。
【数据范围】
1≤N≤10000,
1≤M≤20
【输入样例】
100
2【输出样例】
68【解题思路】
DFS剪枝的经典问题:
1.剪枝一:蛋糕由上到下的半径和高度逐渐递减,所以可以初始化一个每层的最小半径和最小高度。
2.剪枝二:当前摆放的体积若是加上当前能放的最小体积还大于要求体积。说明这个体积不合法(过大),若是已经求出的体积加上我们能够尽可能少的最小侧面积比当前最优解还大,说明该分支一定走不到最优解。
3.剪枝三:从下往上搜,先枚举大的半径或高度,从小的分枝开始搜索。
4.剪枝四:s + 2 * (n - v) / R[m + 1] >= ans ,和 s + sqrt(n - v) * 2 >= ans,得分别从计算公式的角度进行放缩剪枝。
【Python程序代码】
n = int(input())
m = int(input())
sumv,sums = [0]*(m+5),[0]*(m+5)
for i in range(1,m+1):
sumv[i] += sumv[i-1] + i*i*i
sums[i] += sums[i-1] + i*i
r,h = [0]*(m+5),[0]*(m+5)
r[m+1]=h[m+1]=1000000000
ans = 1e9
def dfs(u,nv,ns):
global ans
if u==0:
if nv==n:ans = min(ans,ns)
return
if nv+sumv[u]>n:return
if ns + sums[u]>=ans:return
if ns + (n-nv)//r[u+1]*2>=ans:return
if ns + 2*(n-nv)**0.5>=ans:return
for i in range( min(r[u+1]-1, int(((n-nv)//u)**0.5)),u-1,-1):
for j in range( min(h[u+1]-1, int((n-nv)/i/i)),u-1,-1):
t = 0
if u==m:t=i*i
r[u]=i; h[u]=j
dfs(u-1,nv+i*i*j,ns+2*i*j+t)
dfs(m,0,0)
if ans==1e9:print(0)
else:print(ans)