目录
1 131. 分割回文串
2 51. N 皇后
菜鸟做题,语言是 C++,感冒好了 ver.
1 131. 分割回文串
题眼:给你一个字符串 s,请你将 s 分割 成一些子串。
根据题眼可知,我们需要做的是将字符串 s 连续分割 为几段,并且 每段 都应该是回文串。而非对字符串 s 任意截取,使得截取出的部分都是回文串。
值得注意的是,单个字符也被算作回文串。
解题思路:
- 设置变量 begin 作为子串的开头,end = begin 作为子串的结尾
- 判断 begin 和 end 之间的内容(即子串)是否是回文串
- 若是,则将 begin 移至 end 后面,然后递归处理第二个子串
- 反之,则 end++,继续判断 begin 和 end 之间的内容(即子串)是否是回文串
为什么将 begin 移至 end 后面?因为 end 前面的字母是属于前一个子串的,下一个子串只能接在前一个子串的后面。
递归返回条件:字符串 s 被遍历完毕时,
- ① 可能找出了一组符合题目要求的分割结果,立即返回
- ② 也可能找不到一组符合题目要求的分割结果,不得不返回
返回到上一层函数后,让 end 继续向后移动,以寻找新的回文串,即新的分割方式。若找到新的回文串,则又递归进入下一层,处理下一个子串。
思路说明图:观看顺序是从左到右,从上到下

第一层函数的功能是找出第一个回文串。由于 "a" 是回文串,因此接着递归寻找第二个回文串。第二层函数的功能是找出第二个回文串。由于 "a" 是回文串,因此也接着递归寻找第三个回文串。以此类推。当对整个字符数组处理完毕时,递归层层返回。
重新回到第一层函数,上次我们找的是 "a",那么这次 end + 1,判断 "aa" 是否是回文串。由于 "aa" 是回文串,因此接着递归寻找第二个回文串。以此类推。
本题中的 “选择”,是指从 “可能的回文串” 中选择。比如:第一层函数能分割出的回文串不止一种,它可以是 "a" 也可以是 "aa",因此 end 要不断后移以遍历所有可能的选择。
class Solution {
public:
vector<vector<string>> ans;
vector<string> son;
void helper(string s, int begin) {
if (begin == s.size()) {
ans.push_back(son);
return;
}
for (int end = begin; end < s.size(); ++end) {
if (isPalindrome(s, begin, end)) {
son.push_back(s.substr(begin , end - begin + 1));
helper(s, end + 1);
son.pop_back();
}
}
}
bool isPalindrome(string s, int p, int q) {
while (p <= q) {
if (s[p++] != s[q--])
return false;
}
return true;
}
vector<vector<string>> partition(string s) {
helper(s, 0);
return ans;
}
};说明:判断当前分割出的字符串是否为回文串,代码如下:
bool isPalindrome(string s, int p, int q) {
while (p <= q) {
if (s[p++] != s[q--])
return false;
}
return true;
}其实就是从左往右和从右往左的字母要一样。
2 51. N 皇后
思路说明图:
![]()
解题思路:
模仿 46. 全排列,将棋盘的每一行视为一个坑位,将每一行的每个格子视为一种选择。
Q:如何判断当前格子是否可以填入皇后?
A:根据 c、r - c 和 r + c 来判断。
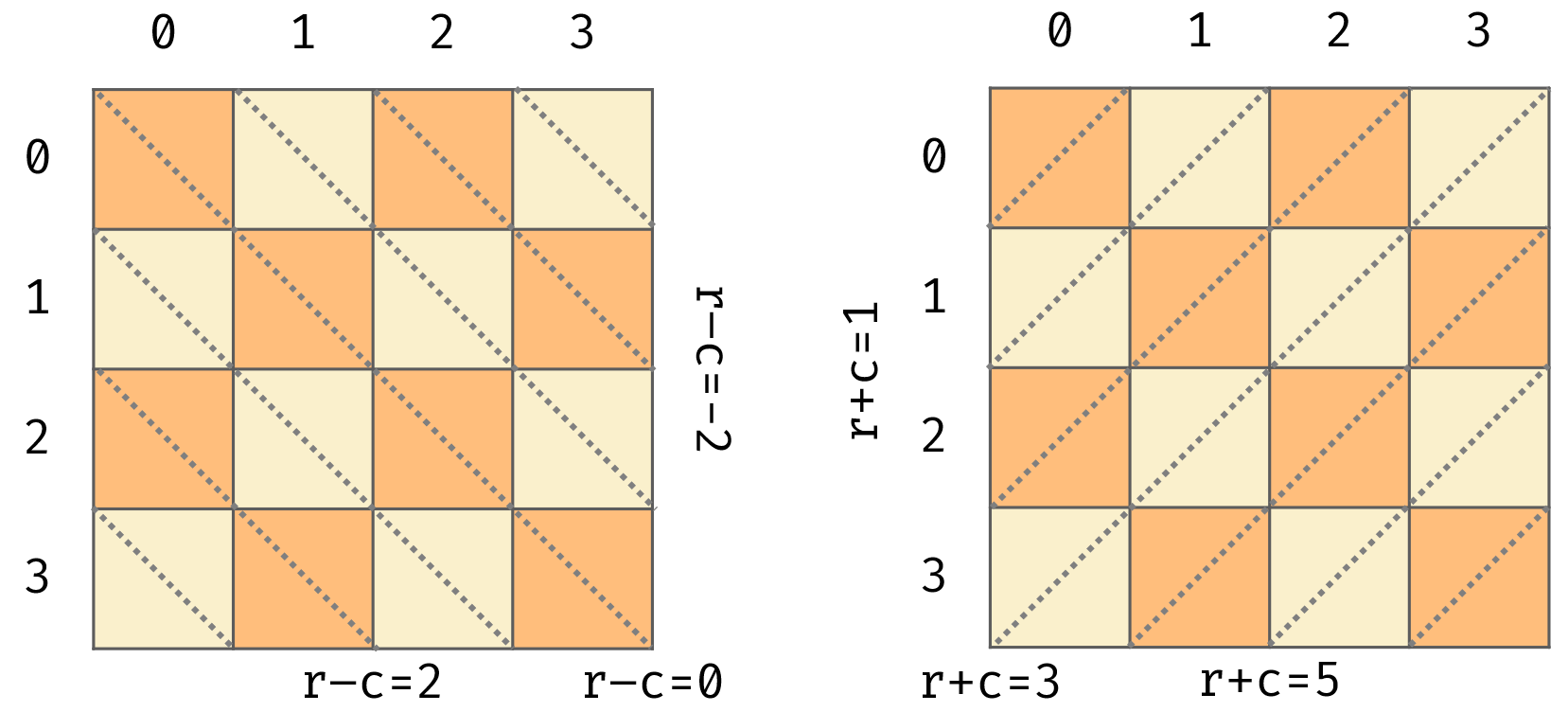
位于同一主对角线上的棋格的 r - c 相同,位于同一副对角线上的棋格的 r + c 相同。因此,每填入一个皇后,我们记录它的 c、r - c 和 r + c,以避免新皇后与其产生冲突。
class Solution {
public:
unordered_set<int> cols, diag1, diag2;
vector<string> output;
vector<vector<string>> ans;
void helper(vector<string> & output, int n, int r) {
if (r == n) {
ans.push_back(output);
return;
}
for (int c = 0; c < n; ++c) {
if (cols.count(c) || diag1.count(r - c) || diag2.count(r + c))
continue;
output[r][c] = 'Q';
cols.insert(c);
diag1.insert(r - c);
diag2.insert(r + c);
helper(output, n, r + 1);
output[r][c] = '.';
cols.erase(c);
diag1.erase(r - c);
diag2.erase(r + c);
}
}
vector<vector<string>> solveNQueens(int n) {
for (int i = 0; i < n; ++i) {
string s (n, '.');
output.push_back(s);
}
helper(output, n, 0);
return ans;
}
};说明:判断当前格子是否可以填入皇后的代码如下:
if (cols.count(c) || diag1.count(r - c) || diag2.count(r + c))
continue;使用三个集合 cols、diag1 和 diag2 分别记录 c、r - c 和 r + c,若当前棋格的位置信息与其中的值重复,则跳过该棋格。