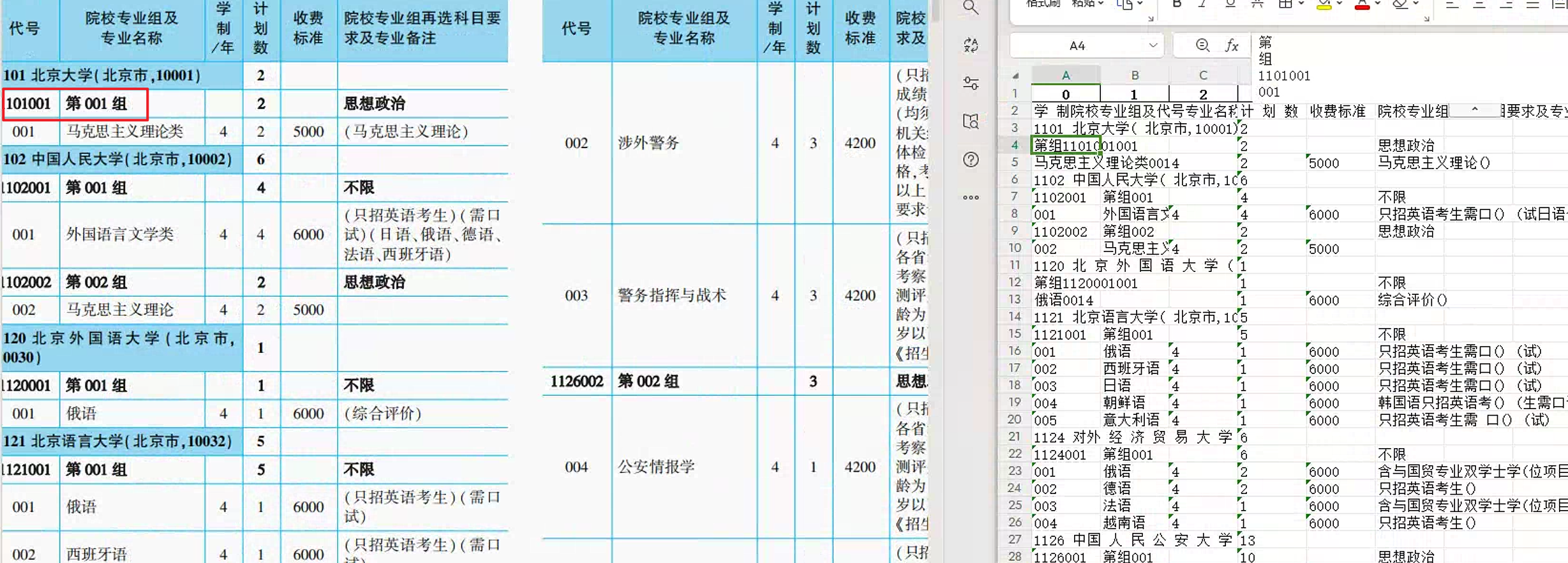
题目

思路

--暴力递归全组合的方法。只有4个数，4种计算方式，共有4 * 3 * 2 * 1 * 4种不同的情况，可以写递归来实现。

--每次计算都是两个数之间的运算，因此4个数需要3次计算，第一次计算前有4个数，第二次有3个数，第三次有两个数，那么怎么在数组长度恒为4时，将每次计算需要使用的数字个数减少呢，就可以将a[0]来记录n个数的最后一个数的值，让前面n个数始终为有效数字。

代码

#include <iostream>
#include <vector>
#include <cmath>
using namespace std;

int a[4];
int maxr;

void dg(int n){
    if (n == 1){
        if (a[0] <= 24){
            maxr = max(maxr, a[0]);
        }
        return;
    }
    else{
        for (int i = 0; i < n - i; i++){
            for (int j = i + 1; j < n; j++){ //双重循环，正好是4 * 3 * 2 * 1种可能。 
                int b1 = a[i];
                int b2 = a[j]; //找a[i]和a[j]的替身。 
                
                a[j] = b1 + b2;
                a[i] = a[n - 1]; //将a[i]和最后一个数替换，使得有效数字逐渐减少，非常巧妙的方法。 
                dg(n - 1);
                a[j] = b1 - b2;
                a[i] = a[n - 1]; //每个递归的前面都要重新确定a[i]的值，上一次递归结束后，a[i]的值很可能改变。 
                dg(n - 1);
                a[j] = b2 - b1;
                a[i] = a[n - 1];
                dg(n - 1);
                a[j] = b1 * b2;
                a[i] = a[n - 1];
                dg(n - 1);
                if (b2 != 0 && b1 % b2 == 0){ //除数不能为0！ 
                    a[j] = b1 / b2;
                    dg(n - 1);
                }
                if (b1 != 0 && b2 % b1 == 0){
                    a[j] = b2 / b1;
                    dg(n - 1);
                }
                
                a[i] = b1;
                a[j] = b2;
            }
        }
    }
}
int main(){
    int n;
    cin >> n;
    for (int i = 0; i < n; i++){
        maxr = 0; //每次循环，都要将其定为0，否则以后输出的都是最大值 
        for (int j = 0; j < 4; j++){
            cin >> a[j];
        }
        dg(4);
        cout << maxr << endl;
    }
    
    return 0;
}