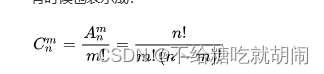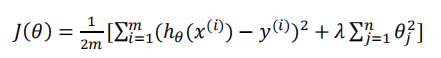🤡博客主页:Code_文晓
🥰本文专栏:数据结构与算法
😻欢迎关注:感谢大家的点赞评论+关注,祝您学有所成!
✨✨💜💛想要学习更多数据结构与算法点击专栏链接查看💛💜✨✨
前面我们学习了许多种类的排序,这次我们学习一种不同思想的排序种类——桶思想排序。桶排序有什么不同吗?如果说前面的排序主要是通过关键字的比较和记录的移动,而桶思想的排序往往并不需要进行关键字的比较。如果大家还不了解桶排序的思想,推荐大家一定要先快速看一下这篇很简单的文章《桶除了能装饭还能排序?》
这节课我们将学习一下桶思想排序中的计数排序和基数排序算法,让我们开始这次的学习旅程吧。
1. 计数排序
计数排序是通过计数而不是比较来进行排序的。算法比较简单,适合于待排序记录数量多但排序关键字的范围比较小的整数数字排序情形。
计数排序,这种排序算法是利用数组下标来确定元素的正确位置的。 假设数组中有10个整数,取值范围为0~10,要求用最快的速度把这10个整数从小到大进行排序。 可以根据这有限的范围,建立一个长度为11的数组。数组下标从0到10,元素初始值全为0。

假设数组数据为:{ 9,1,2,7,8,1,3,6,5,3 }
下面就开始遍历这个无序的随机数列,每一个整数按照其值对号入座,同时,对应数组下标的元素进行 加1操作 例如第1个整数是9,那么数组下标为9的元素加1

最终,当数列遍历完毕时,数组的状态如下:

该数组中每一个下标位置的值代表数列中对应整数出现的次数 直接遍历数组,输出数组元素的下标值,元素的值是几,就输出几次,0不输出。 则顺序输出是:1、1、2、3、3、5、6、7、8、9
计数排序如果起始数不是从0开始,比如分数排序: 95,94,91,98,99,90,99,93,91,92 数组起始数为90,这样数组前面的位置就浪费了。又或者说,如果遇到要排序的数字是负数呢?
所以为了解决这个问题,也不要紧,我们确定要排序的整数数字的最大值和最小值从而确定出计数数组定义多大合适。当然,在根据计数数组来输出排序结果时,计数数组下标为0的元素代表的应该是待排序关键字中的最小值,而不再是0本身。比如,对-10到10之间的元素排序,定义的计数数组大小应该是21(最大值-最小值+1)。而计数数组下标为0的元素代表的应该是-10。
有了上述讲解之后,下面就是计数排序的代码实现:
// 计数排序
void CountSort(int* myarray, int length)
{
// 找出数组的最小值和最大值
int min = myarray[0], max = myarray[0];
for (int i = 0; i < length; i++)
{
if (myarray[i] < min)
{
min = myarray[i];
}
if (myarray[i] > max)
{
max = myarray[i];
}
}
int range = max - min + 1; // 计数数组的范围
int* countA = (int*)malloc(sizeof(int) * range); // 计数数组
memset(countA, 0, sizeof(int) * range); // 初始化计数数组元素都为0
// 计数
for (int i = 0; i < length; i++)
{
countA[myarray[i] - min]++;
}
// 排序
int k = 0;
for (int j = 0; j < range; j++)
{
while (countA[j]--)
{
myarray[k++] = j + min;
}
}
// 释放计数数组
free(countA);
}计数排序算法效率分析
计数排序算法的时间复杂度方面,因为要扫描待排序的 个元素,还需要用到辅助的计数数组来进行计数统计工作,这里用
代表计数数组的大小,所以计数排序算法的时间复杂度为O(
),当然因为
值取值范围比较小,可能远远小于
值,所以也可以把计数排序算法的时间复杂度看成是O(legnth)。因为用到了计数数组,所以,空间复杂度是O(
)。
前面曾经强调过,计数排序的适用场合是:
-
待排序记录数量多。
-
排序关键字的范围比较集中(范围小)。
-
整数数字排序。
此时用计数排序可能比其他排序算法要快得多。但如果不满足这样的场合,则要慎用这样的排序,以免造成排序效率过差。
2. 基数排序
2.1 什么是基数排序
以往的排序主要是通过关键字的比较和记录的移动来进行。而基数排序是一种不同以往的排序方式,它并不需要进行关键字的比较。
基数排序要进行多趟排序,每趟排序都要经历“分配”和“收集”两个步骤,当然,每趟排序也都会基于上一趟排序的成果再次排序。
有这么一组数字 {516,231,445,323,299,2,18,67,42,102,164,755,687,437} 。现在希望对这组数字进行从小到大的排序。观察一下这组数字,最大的数字也就是3位(个位、十位、百位),所以为了更清晰地说明算法,可以把这组数字都扩展成3位的,比如 {516,231,445,323,299,002,018,067,042,102,164,755,687,437} 。
将关键字拆分成d组(上面范围每个数字都是3位,所以将要拆分成3组,即d=3),然后按关键字位的权重递增的次序(个位、十位、百位)来做d趟的“分配”和“收集”动作。
因为“个位”、“十位”、“百位”数字取值都是0~9(10个数字)之间,所以建立10个辅助队列(桶)B0~B9来保存个位、十位、百位信息。
第一趟处理取权重最低的即“个位”进行“分配”和“收集”两个动作,如图1所示。
-
分配:以“个位”数字进行分配,将指定数字放到辅助队列B0~B9中,比如对于数字516,其个位数字是6,所以放入到B6中。其余数字也是如此处理。对于个位数字重复的,在相应的辅助队列中从上到下依次放置。
-
收集:依次从B0~B9辅助队列中把相关的数字从上到下、从左到右收集并排列起来。
这样就得到了按“个位”递增排序的数字序列。

第二趟处理取“十位”进行“分配”和“收集”两个动作,第二趟处理会基于第一趟处理的成果进行,如图2所示。
-
分配:以“十位”数字进行分配,将指定数字放到辅助队列B0~B9中,比如对于数字231,其十位数字是3,所以放入到B3中。其余数字也是如此处理。对于十位数字重复的,在相应的辅助队列中从上到下依次放置。不难发现,在相同的队列中,个位数越小越是在队头位置。
-
收集:依次从B0~B9辅助队列中把相关的数字从上到下、从左到右收集并排列起来。
这样就得到了按“十位”递增排序的数字序列。对于“十位”数字相同的,“个位”数字按递增排序。

第三趟处理取“百位”进行“分配”和“收集”两个动作,第三趟处理会基于第二趟处理的成果进行,如图3所示。
-
分配:以“百位”数字进行分配,将指定数字放到辅助队列B0~B9中,比如对于数字002,其百位数字是0,所以放入到B0中。其余数字也是如此处理。对于百位数字重复的,在相应的辅助队列中从上到下依次放置。
-
收集:依次从B0~B9辅助队列中把相关的数字从上到下、从左到右收集并排列起来。
这样就得到了按“百位”递增排序的数字序列。对于“百位”数字相同的,“十位”数字按递增排序。如果“百位”和“十位”数字都相同,则会按“个位”递增排序。

实现代码如下。
//基数排序
template<typename T>
void RadixSort(T myarray[], int length)
{
if (length <= 1) //不超过1个元素的数组,没必要排序
return;
T* pResult = new T[length]; //新数组,用于保存每趟排序的结果
//借用C++标准库中的list容器保存必要的信息,当然也可以用自己写的链表来保存数据
std::list<T *> mylist[10]; //#include <list> ,注意list中的<>里的数据类型
//3,意味着分别取得个位、十位、百位 数字
for (int i = 0; i < 3; ++i) //为简化代码,假设已经知道待排序数字最大不超过3位,所以这里就直接写i < 3了
{
//(1)分配
for (int j = 0; j < length; ++j)
{
//根据i值来决定取得某个数字的个位、十位、百位
int tmpi = i;
T tmpvalue = myarray[j];
T lastvalue; //取得的个位、十位、百位数字保存在这里
while (tmpi >= 0)
{
lastvalue = tmpvalue % 10;
tmpvalue /= 10;
tmpi--;
} //end while
mylist[lastvalue].push_back(&myarray[j]); //在list尾部插入元素
} //end for j
//(2)收集
int idx = 0;
for (int k = 0; k < 10; ++k)
{
for (auto iter = mylist[k].begin(); iter != mylist[k].end(); ++iter)
{
pResult[idx] = *( * (iter));
idx++;
} //end iter
mylist[k].clear(); //清空mylist,为下次向其中存数据做准备
} //end for k
//(3)把数据拷贝回myarray
for (int m = 0; m < length; ++m)
{
myarray[m] = pResult[m];
}//end for m
} //end for i
delete[] pResult;
return;
}在main主函数中,代码应该是这样的。
int arr[] = { 516, 231, 445, 323, 299, 2, 18, 67, 42, 102, 164, 755, 687, 437 };
int length = sizeof(arr) / sizeof(arr[0]); //数组中元素个数
RadixSort(arr, length);//对数组元素进行基数排序
cout <<"基数排序结果为:";
for (int i = 0; i < length; ++i)
{
cout << arr[i] <<"";
}
cout << endl; //换行
下面是代码的执行结果。

2.2 基数排序算法效率分析
基数排序算法时间复杂度分析:假设算法进行了d趟的分配和收集,每趟分配要扫描待排序的n个元素,所以每一趟分配的时间复杂度是O(n)。此外还需要用到多个辅助队列进行分配完后的数据收集工作,假设用到的是k个辅助队列,所以每趟收集的时间复杂度是O(k)。所以总的时间复杂度是O(d(n+k))。
从代码可以看到,基数排序需要一些辅助空间来保存数据。
比如这段代码行。
T* pResult = new T[length];
std::list<T *> mylist[10];这段代码用到的队列数组有k(10)个,所以空间复杂度是O(n+k)。此外,基数排序算法是稳定的,你只要结合代码,拿两个相同的数字画一画或稍微想想就可以得出结论。
2.3 基数排序算法的应用
前面实现的算法代码是针对一系列数字进行从小到大的排序。当然,基数排序还有许多适用场合。
举个例子,某学校有5000名学生,他们的出生日期有详细记录,要求将学生按照年龄从小到大排序。
要完成这个需求,根据学生的出生日期来确定排序次序是非常合适的,可以把每个学生的出生日期拆解为年、月、日三部分。已知学生的出生日期在1990~2010年之间,月份自然是在1~12之间,日期在1~31之间。
从权重的角度来看,年>月>日,所以,排序的时候应该是先按照日来排序,再按照月来排序,最后按照年来排序。
考虑到按照年龄从小到大排序,所以日这一项应该从大到小排序(日这个数字越大的人年纪越小)。
看一看第一趟先对日这一项进行排序,如图4所示。

第二趟要针对月这一项进行排序,这一项也应该从大到小(月这个数字越大的人年纪越小),如图5所示。

第三趟要针对年这一项进行排序,这一项也应该从大到小(年这个数字越大的人年纪越小),如图6所示。

经过上述三趟的分配和收集操作,就可以得到学生按照年龄递增的排序。从这个范例中可以看到,每趟处理所采用的辅助队列大小是可以不同的。
根据前面的分析,基数排序算法的时间复杂度是O(d(n+k))。里面的字母都是什么意思呢?
-
d表示趟数,这里是3。
-
n是5000,因为参与年龄排序的学生是5000名。
-
k是每趟排序用到的辅助队列大小,第一趟是31,第二趟是12,第三趟是21,这里按最大值31计算。
-
把d、n、k代入时间复杂度公式O(d(n+k)) ≈ O(15093)。相比于一些其他时间复杂度的排序算法比如O($n^{2}$) ≈ O(25000000)或者O(n$log_{2}^{n}$) ≈ O(60000)来说,基数排序算法的时间复杂度表现非常好。
理解基数排序的应用之后,我们尝试总结一下它的适用场合。
-
记录中要排序的关键字可以很方便地拆分成几组,比如上述范例的年、月、日是三组。组数当然也不能太大,因为每多一组就代表多一趟分配和收集处理。
-
每组关键字的取值范围也不应该太大,比如上述范例年月日的取值范围都不算大。否则算法需要的辅助空间也会太大导致空间复杂度过高。
-
待排序记录数量多多益善,记录数量多意味着要排序的元素数量n较多。如果待排序记录很少,则没有必要用基数排序,基数排序毕竟需要不少的辅助空间,杀鸡焉用牛刀。
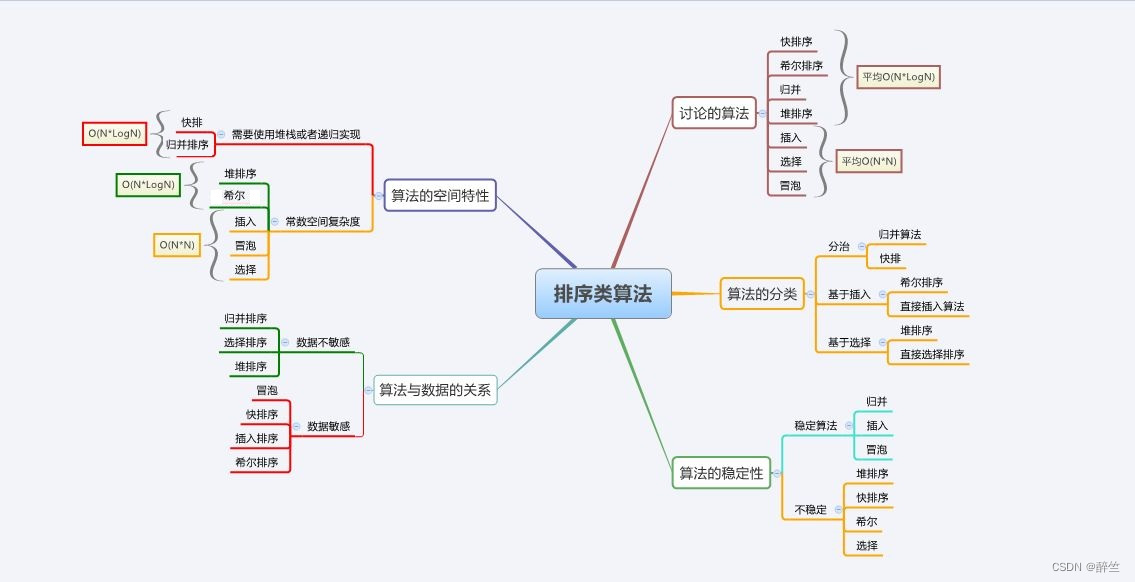
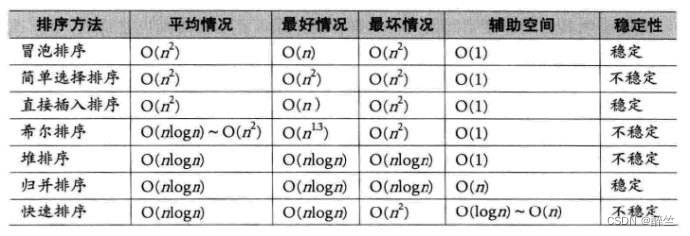
3. 常见排序算法复杂度及稳定性汇总
学习到这里,如果你觉得本篇文章对你有一点帮助的话,希望您能点个赞或评论支持一下~