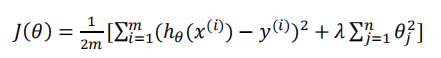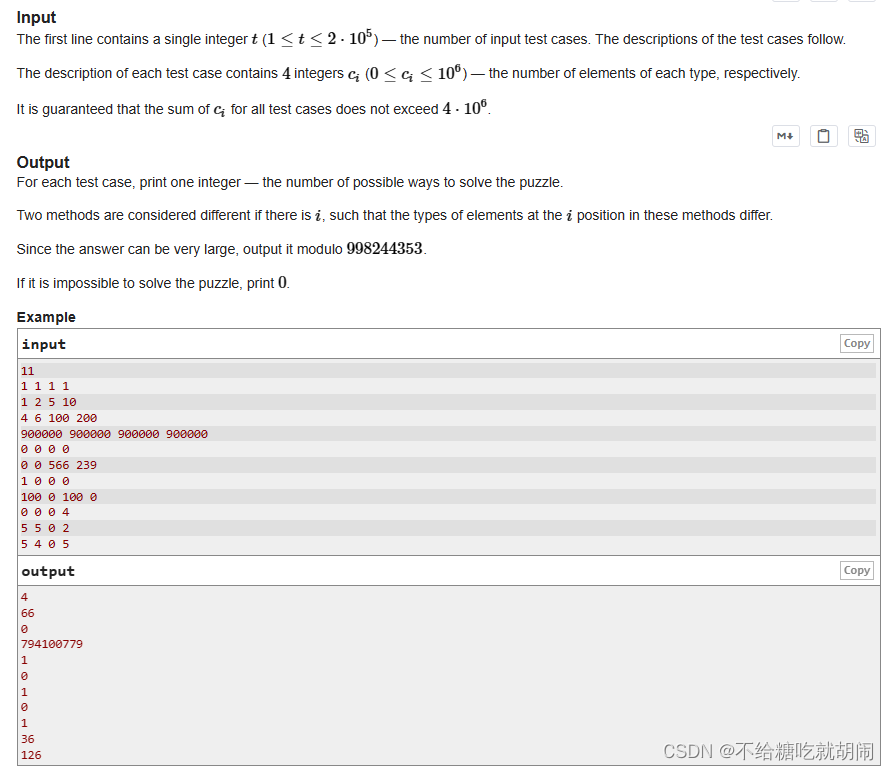
解析：

本体是进行分类讨论这么才使全部的拼图用完，且可以合成多个种类。

列举其所有可以拼成的方法个数：

第一种：3 3 3 3 

第二种： 4 4 4 4 

第三种：1 2 1 2

第四种：1 3 3 2

第五种：2 4 4 1

对于第一种第二种3的个数和4个个数在不考虑的情况下。

只靠路1 2 的个数即可。

当 1 和2 相差个数超过 1时，答案为 0；

我们可以 当1 比 2 大一个时，有 a个1 c个 2 时，有 a个位置可以放3个，a个 位置可以放 4的

当时a为位置有区别的，但是放进去的3没有区别的。

往a个有区别的盒子当中放入c个无区别的小球。

使用a-1个隔板，进行隔开，刚好就是 a个位置 。

等价于 先在每个盒子中放入 n个小球，后面在取出来。
n+m小球 有 n+m-1个空隙。

l理论知识：

求组合数模板：

求逆元：

剩下的就是组合数学公式：

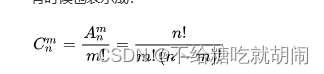
代码:

https://www.luogu.com.cn/problem/P1709
    #include <iostream>
    #include <vector>
    #include <set>
    #include <queue>
    #include <algorithm>
     
    using namespace std;
     
    typedef long long ll;
     
    const int mod = 998244353;
     
    ll pow_mod(ll x, ll p) { // 逆元 
        if (p == 0) {
            return 1;
        }
        if (p % 2 == 0) {
            ll y = pow_mod(x, p / 2);
            return (y * y) % mod;
        }
        return (x * pow_mod(x, p - 1)) % mod;
    }
     
    ll inv(ll x) { //直接求逆元 mod - 2 
        return pow_mod(x, mod - 2); //x == x^p-2(mod p)
    }
     
    vector<ll> fact = {1};
     
    ll cnk(ll n, ll k) {
        ll res = fact[n];
        res = (res * inv(fact[k])) % mod;
        res = (res * inv(fact[n - k])) % mod;
        return res;
    }
     
    ll calc(int n1, int n2, int n3, int n4) {
        return (cnk(n1 + n3 - 1, n3) * cnk(n2 + n4 - 1, n4)) % mod;
    }
     
    void solve() {
        int n1, n2, n3, n4;
        cin >> n1 >> n2 >> n3 >> n4;
        if (n1 + n2 == 0) {
            cout << (n3 == 0 || n4 == 0 ? 1 : 0) << '\n';
            return;
        }
        if (abs(n1 - n2) > 1) {
            cout << "0\n";
            return;
        }
        ll res = 0;
        if (n1 <= n2) { // n1 <= n2  
            res += calc(n1 + 1, n2, n3, n4);
        }
        if (n2 <= n1) {
            res += calc(n1, n2 + 1, n3, n4);
        }
        cout << res % mod << '\n';
    }
     
    int main() {
        for (ll i = 1; i <= 4e6; ++i) {
            fact.push_back((fact.back() * i) % mod);
        }
        int t;
        cin >> t;
        for (int _ = 0; _ < t; ++_) {
            solve();
        }
    }