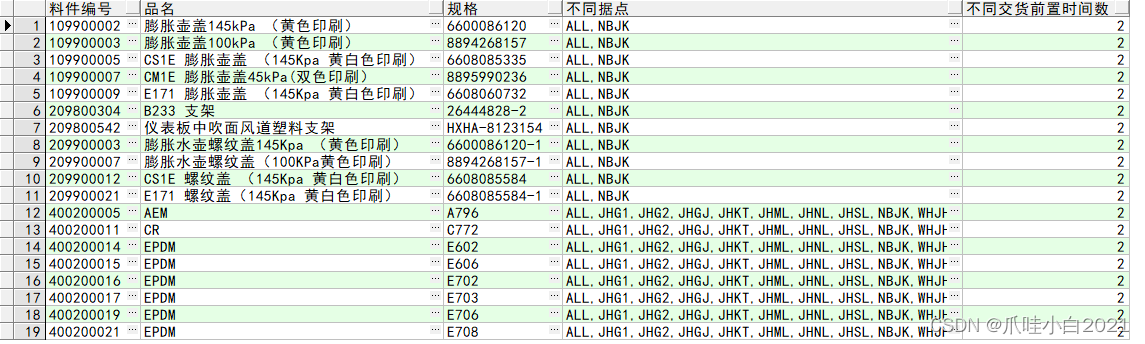
Pytorch常用的函数(七)空洞卷积详解
1 初识空洞卷积
1.1 空洞卷积与语义分割任务
语义分割面临的困境:
-
与检测模型类似,语义分割模型也是建立是分类模型基础上的,即利用CNN网络来提取特征进行分类。在CNN分类模型中,一般情况下会通过stride>1的卷积层或者池化层进行降采样,此时特征图维度降低,但是特征更高级,语义更丰富。
- 这对于简单的分类没有问题,因为最终只预测一个全局概率。
- 对于图像分割模型就无法接受,因为我们需要给出图像不同位置的分类概率,特征图过小时会损失很多信息。对于前面的特征图,其保持了较多的空间位置信息,虽然语义会差一些,但是这些空间信息对于精确分割也是至关重要的。
- 其实对于目标检测模型同样存在这个问题,但是由于检测比分割更粗糙,所以图像分割对于这个问题更严重。
-
但是下采样层又是不可缺少的。
- 首先stride>1的下采样层对于提升感受野非常重要,这样高层特征语义更丰富,而且对于分割来说较大的感受野也至关重要;
- 另外的一个现实问题,没有下采样层,特征图一直保持原始大小,计算量是非常大的。
-
总之,这是语义分割所面临的一个困境或者矛盾,也是大部分研究要一直解决的。
语义分割任务的两种解决方案:
语义分割任务主要存在两种不同的解决方案:
- 一种是EncoderDecoder结构,其中Encoder就是下采样模块,负责特征提取,而Decoder是上采样模块(通过插值,转置卷积等方式),负责恢复特征图大小,经典的网络如U-Net(网络结构如下图)、U2-Net等。而要直接将高层特征图恢复到原始大小是相对困难的,所以Decoder是一个渐进的过程,而且要引入横向连接(lateral connection),即引入低级特征增加空间信息特征分割准确度。

- 另外一种结构是DilatedFCN,主要是通过空洞卷积(Atrous Convolution)来
减少下采样率,但是又可以保证感受野。例如利用空洞卷积,那么我们就可以让原图的下采样倍数仅为8,那么最终的特征图语义不仅语义丰富而且相对精细,可以直接通过插值恢复原始分辨率。DeepLab系列网络(如下图)就是属于典型的DilatedFCN。

1.2 空洞卷积的相关
1.2.1 空洞卷积的理解
- 空洞卷积(Atrous Convolution),又称膨胀卷积或扩张卷积。
- 空洞卷积可以在增加感受野的同时保持特征图的尺寸不变,从而代替下采样和上采样操作。
- 与正常的卷积不同的是,空洞卷积引入了一个称为
扩张率(dilation rate)的超参数,该参数定义了卷积核处理数据时各值的间距。扩张率,也称空洞数(Hole Size)。
下图是我们熟悉的标准卷积(k=3,p=1,s=2,r=1)

下图是扩张率为2空洞卷积(k=3,p=0,s=2,r=2)

1.2.2 空洞卷积感受野的计算
扩张率(dilation rate)定义了卷积核处理数据时各值的间距
设空洞卷积的卷积核大小为
k
,
空洞数为
d
,等效卷积核大小为
k
′
k
′
=
k
+
(
k
−
1
)
×
(
d
−
1
)
设当前层感受野为
R
F
i
+
1
,上一层感受野为
R
F
i
R
F
i
+
1
=
R
F
i
+
(
k
′
−
1
)
×
S
i
S
i
表示之前所有层步长的乘积
(
不包括当前层
)
,因此当前层步长不影响当前层的感受野。另外,感受野和
p
a
d
d
i
n
g
无关。
设空洞卷积的卷积核大小为k,空洞数为d,等效卷积核大小为k' \\ k' = k + (k-1)×(d-1) \\ 设当前层感受野为RF_{i+1},上一层感受野为RF_{i} \\ RF_{i+1} = RF_{i} + (k'-1)× S_i \\ S_i表示之前所有层步长的乘积(不包括当前层),因此当前层步长不影响当前层的感受野。另外,感受野和padding无关。
设空洞卷积的卷积核大小为k,空洞数为d,等效卷积核大小为k′k′=k+(k−1)×(d−1)设当前层感受野为RFi+1,上一层感受野为RFiRFi+1=RFi+(k′−1)×SiSi表示之前所有层步长的乘积(不包括当前层),因此当前层步长不影响当前层的感受野。另外,感受野和padding无关。
例子1:从左到右分别为a、b、c子图,三幅图是相互独立进行卷积的,大框表示输入图像(感受野默认为1),深绿色表示
3
×
3
3×3
3×3的卷积核,绿色区域表示卷积后的感受野。
- a是普通的卷积过程(dilation rate = 1),卷积后的感受野为3;
- b是dilation rate = 2的空洞卷积,卷积后的感受野为5;
- c是dilation rate = 3的空洞卷积,卷积后的感受野为7;
- 普通卷积是空洞卷积的一种特殊情况。
- 我们可以明显的看到,
在卷积核不变的情况下,增加扩张率可以增加感受野。

例子2:请注意下图和上面的图有区别,上图的三幅图是独立的,而下图是从左到右连续进行卷积。
- 第一层卷积,为普通卷积,经过第1层卷积,感受野为3;
- 第二层卷积,先算等效卷积核为 k ′ = k + ( k − 1 ) × ( d − 1 ) = 3 + ( 3 − 1 ) × ( 2 − 1 ) = 5 k'=k + (k-1)×(d-1)=3+(3-1)×(2-1)=5 k′=k+(k−1)×(d−1)=3+(3−1)×(2−1)=5,然后计算感受野 R F i + 1 = R F i + ( k ′ − 1 ) × S i = 3 + ( 5 − 1 ) × 1 = 7 RF_{i+1} = RF_{i} + (k'-1)× S_i=3+(5-1)×1=7 RFi+1=RFi+(k′−1)×Si=3+(5−1)×1=7,因此经过第3层卷积,感受野为7;
- 第三层卷积,先算等效卷积核为 k ′ = k + ( k − 1 ) × ( d − 1 ) = 3 + ( 3 − 1 ) × ( 4 − 1 ) = 9 k'=k + (k-1)×(d-1)=3+(3-1)×(4-1)=9 k′=k+(k−1)×(d−1)=3+(3−1)×(4−1)=9,然后计算感受野 R F i + 1 = R F i + ( k ′ − 1 ) × S i = 7 + ( 9 − 1 ) × 1 = 15 RF_{i+1} = RF_{i} + (k'-1)× S_i=7+(9-1)×1=15 RFi+1=RFi+(k′−1)×Si=7+(9−1)×1=15,经过第3层卷积,感受野为15。

经过上述例子,我们已经知道空洞卷积可以增大感受野,那么如何理解可以不改变图像输出特征图的尺寸呢?
我们来看下标准卷积计算特征图尺寸的公式:
设输入特征图为
(
H
,
W
)
,
卷积核大小为
(
K
,
K
)
,
填充为
P
,步长为
S
,输出为
O
H
,
O
W
O
H
=
H
+
2
P
−
K
S
+
1
O
W
=
W
+
2
P
−
K
S
+
1
设输入特征图为(H,W),卷积核大小为(K,K),填充为P,步长为S,输出为OH,OW \\ OH=\frac{H+2P-K}{S} + 1 \\ OW=\frac{W+2P-K}{S} + 1 \\
设输入特征图为(H,W),卷积核大小为(K,K),填充为P,步长为S,输出为OH,OWOH=SH+2P−K+1OW=SW+2P−K+1
- 从上述影响特征图尺寸的参数中可以看到没有扩张率,而标准卷积和空洞卷积之间的区别就是扩张率不同,所以
使用空洞卷积可以不改变图像输出特征图的尺寸。不过,天下没有免费的午餐,保持分辨率意味着较大的运算量。 需要注意的是,在空洞卷积里面,上面式子中的K为等效的卷积核,想要输入和输出不变,需要填充。- 一般每一层的卷积核都是用3 x 3 大小的,而每一层只要设置不同dilation rate时,感受野就会不一样,也即获取了多尺度信息。当然这样操作并不影响特征图的尺寸,这样一来,又避免下采样那样造成信息损失,同时也利用到多尺度信息。
1.2.3 pytorch中API
Dilation_conv2d = nn.Conv2d(
in_channels = in_channels,
out_channels = out_channels,
kernel_size = kernel_size ,
stride = stride,
padding=padding,
dilation=dilation # 设置扩张率
)
- 默认dilation=1,所以我们在使用二维卷积的时候,如果不去设置dilation,默认都是使用标准卷积。
import torch
import torch.nn as nn
input_data = torch.randn(1, 3, 64, 64)
dilated_conv1 = nn.Conv2d(in_channels=3,
out_channels=64,
kernel_size=3,
dilation=2,
padding=2, # 设置dilation=2后,等效卷积核kernel_size=5,因此设置padding=2
stride=1)
output = dilated_conv1(input_data)
print("Input shape:", input_data.shape)
print("Output shape:", output.shape)
Input shape: torch.Size([1, 3, 64, 64])
Output shape: torch.Size([1, 64, 64, 64])
2 空洞卷积的问题与优化
2.1 空洞卷积存在的问题
2.1.1 栅格效应 Gridding Effect
- 假设我们仅仅多次叠加dilation rate为均为2的3 x 3 kernel 的话,则会出现这个问题。
- 左侧从下往上看,相当于一个卷积网络,每次卷积采用
膨胀率为 2的空洞卷积; - 右侧是卷积后的统计分析,整个图代表原始输入,每个格子代表一个像素,格子里的值代表3次卷积后,该像素被计算的次数;
- 可以看到有些像素是没有参与计算的,造成了大量的信息丢失,影响最终效果。
- 左侧从下往上看,相当于一个卷积网络,每次卷积采用
- 由于空洞卷积的计算方式类似于棋盘格式,某一层得到的卷积结果,来自上一层的独立的集合,没有相互依赖,因此该层的卷积结果之间没有相关性,即局部信息丢失。这对 pixel-level dense prediction 的任务来说是致命的。

2.1.2 Long-ranged information might be not relevant
- 我们从dilated convolution 的设计背景来看就能推测出这样的设计是用来获取 long-ranged information。然而,只采用大 dilation rate 的信息或许只对一些大物体分割有效果,而对小物体来说可能则有弊无利了。如何同时处理不同大小的物体的关系,则是设计好 dilated convolution 网络的关键。
- 由于空洞卷积稀疏的采样输入信号,使得远距离卷积得到的信息之间没有相关性,影响分类结果。
2.2 HDC方案解决空洞卷积存在的问题
论文地址:https://arxiv.org/abs/1702.08502
规则1 第二层的两个非零元素之间的最大距离小于等于该层卷积核的大小,
即
M
2
<
K
即M_2<K
即M2<K
M
i
=
m
a
x
[
M
i
+
1
−
2
r
i
,
M
i
+
1
−
2
(
M
i
+
1
−
r
i
)
,
r
i
]
M
i
:第
i
层两个非零元素之间的最大距离
r
i
:
第
i
层的扩张率
最后一层
M
n
=
r
n
M_i = max[M_{i+1}-2r_i, M_{i+1}-2(M_{i+1}-r_i),r_i ] \\ M_i:第i层两个非零元素之间的最大距离 \\ r_i:第i层的扩张率 \\ 最后一层M_n = r_n
Mi=max[Mi+1−2ri,Mi+1−2(Mi+1−ri),ri]Mi:第i层两个非零元素之间的最大距离ri:第i层的扩张率最后一层Mn=rn
公式比较难理解,举例如下:
参数
K
=
3
,
r
=
[
1
,
2
,
5
]
,
此时
M
3
=
r
3
=
5
M
2
=
m
a
x
[
M
3
−
2
r
2
,
M
3
−
2
(
M
3
−
r
2
)
,
r
2
]
=
m
a
x
[
5
−
4
,
5
−
2
(
5
−
2
)
,
2
]
=
2
此时
M
2
<
3
,满足规则,因此这样设置扩张率不会出现栅格效应问题。
假如此时
r
=
[
1
,
2
,
9
]
,那么此时
M
3
=
r
3
=
9
M
2
=
m
a
x
[
M
3
−
2
r
2
,
M
3
−
2
(
M
3
−
r
2
)
,
r
2
]
=
m
a
x
[
9
−
4
,
9
−
2
(
9
−
2
)
,
2
]
=
5
此时
M
2
>
3
,不满足规则,因此这样设置扩张率会出现栅格效应问题。
参数K=3,r=[1,2,5],此时M_3=r_3=5 \\ M_2 = max[M_{3}-2r_2, M_{3}-2(M_{3}-r_2),r_2 ] \\ =max[5-4,5-2(5-2),2]=2 \\ 此时M_2 < 3,满足规则,因此这样设置扩张率不会出现栅格效应问题。\\ 假如此时r=[1, 2, 9],那么此时M_3=r_3=9 \\ M_2 = max[M_{3}-2r_2, M_{3}-2(M_{3}-r_2),r_2 ] \\ =max[9-4,9-2(9-2),2]=5\\ 此时M_2 > 3,不满足规则,因此这样设置扩张率会出现栅格效应问题。\\
参数K=3,r=[1,2,5],此时M3=r3=5M2=max[M3−2r2,M3−2(M3−r2),r2]=max[5−4,5−2(5−2),2]=2此时M2<3,满足规则,因此这样设置扩张率不会出现栅格效应问题。假如此时r=[1,2,9],那么此时M3=r3=9M2=max[M3−2r2,M3−2(M3−r2),r2]=max[9−4,9−2(9−2),2]=5此时M2>3,不满足规则,因此这样设置扩张率会出现栅格效应问题。
规则2:扩张系数从1开始设置
其实这也不算做一个规则,但原论文中都是从1开始的。
规则3:扩张系数的公约数不能大于1
如果设置扩张系数为[2,4,8],他们之间的公约数为2,大于1了,仍然会出现gridding effect的问题。
另外还有一个建议:将扩张系数设置为锯齿形状[1,2,3,1,2,3]
参考链接如下:
关于HDC可以参考B站up主[霹雳吧啦Wz]视频:https://www.bilibili.com/video/BV1Bf4y1g7j8
膨胀卷积-空洞卷积-Dilated Convolution
深入理解空洞卷积