常见排序及查找算法

内容引用自：
【数据结构和算法】十大经典排序算法（动图演示）

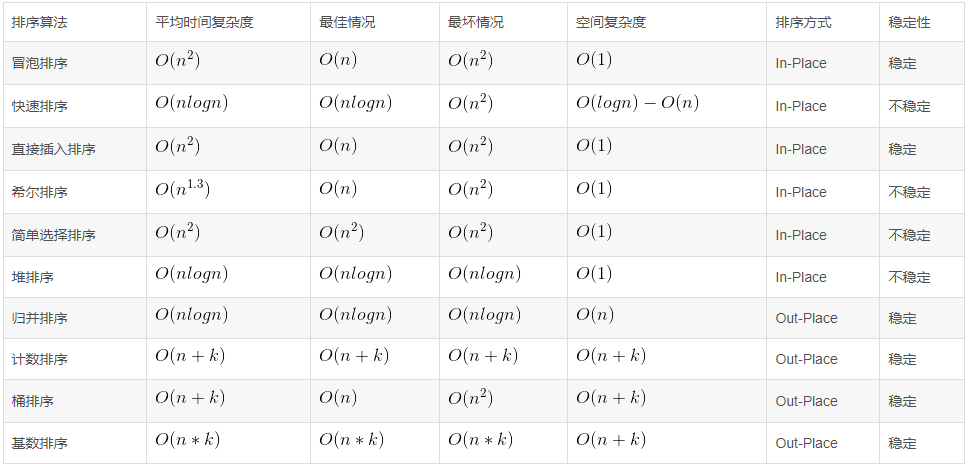
算法复杂度

在这里插入图片描述

1、冒泡排序

1.1、动图演示

遍历列表数据，共遍历length(列表)次，每一次的遍历都要从左到右进行两两比对，左边比右边小，那么值就调换，否则进行往后两位的比对值；
每遍历一次，可以得到一个最大值（第一次遍历时最大值，后面遍历得到的应该叫次最大值）

在这里插入图片描述

1.2、代码

def bubble_sort(arr):
    for i in range(len(arr)):
        for j in range(len(arr) - 1 - i):
            if arr[j] > arr[j+1]:
                tmp = arr[j]
                arr[j] = arr[j+1]
                arr[j+1] = tmp
            # # print(arr)
            print(arr)

    return arr


if __name__ == '__main__':
    bubble_sort([9, 8, 7, 6, 5, 4, 3, 2, 1])

2、快速排序

2.1 、核心思想：

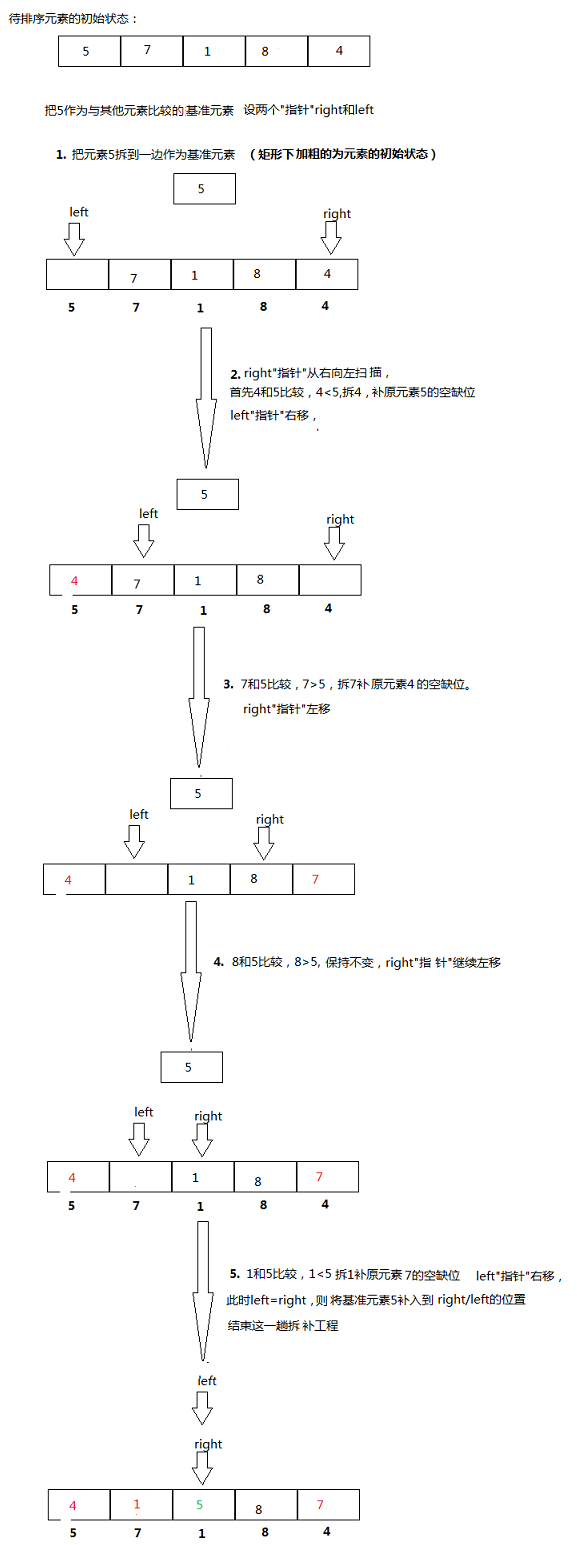
在待排序的元素任取一个元素作为基准(通常选第一个元素(arr[left])，称为基准元素(pivot)，）
将待排序的元素进行分块，比基准元素大的元素移动到基准元素的右侧，比基准元素小的移动到作左侧，从而一趟排序过程，就可以锁定基准元素的最终位置
对左右两个分块重复以上步骤直到所有元素都是有序的（递归过程）

2.2、静态图（来源：图解快速排序），动图不那么好理解：

2.3、代码：

def quick_sort(arr, left, right):
    print("原始数据：\n" + str(arr))

    if left >= right:
        return

    i = left
    j = right
    pivot = arr[left]

    while i != j:
        while (i < j) and arr[j] > pivot:  # 这里不可以等于，等于会导致1，2，1的情况，无法实现排序
            j -= 1
            
        # 比pivot小， 就将小的值替换到pivot前面去，交换值
        p = arr[i]
        arr[i] = arr[j]
        arr[j] = p

        print(arr)

        # 因为上一步arr[j]与arr[i]值调换以后，arr[i]一定是比小的，所以不用提前 i += 1，下方的while会自动给执行一次i += 1
        while (i < j) and arr[i] <= pivot:
            i += 1
		
		# 比pivot大， 就将大的值替换到pivot后面去，交换值
        p = arr[i]
        arr[i] = arr[j]
        arr[j] = p

        print(arr)

    quick_sort(arr, left, i - 1)
    quick_sort(arr, i+1, right)

    return


print(quick_sort([3, 6, 8, 10, 1, 2, 1], 0, 6))
# print(quick_sort([6, 6, 8, 10, 1, 2, 1], 0, 6))
# print(quick_sort([6, 6, 6, 10, 1, 2, 1], 0, 6))
# print(quick_sort([9, 8, 7, 6, 5, 4, 3], 0, 6))

2.4、结果：

原始数据：
[3, 6, 8, 10, 1, 2, 1]
[1, 6, 8, 10, 1, 2, 3]
[1, 3, 8, 10, 1, 2, 6]
[1, 2, 8, 10, 1, 3, 6]
[1, 2, 3, 10, 1, 8, 6]
[1, 2, 1, 10, 3, 8, 6]
[1, 2, 1, 3, 10, 8, 6]
[1, 2, 1, 3, 10, 8, 6]
[1, 2, 1, 3, 10, 8, 6]
原始数据：
[1, 2, 1, 3, 10, 8, 6]
[1, 2, 1, 3, 10, 8, 6]
[1, 1, 2, 3, 10, 8, 6]
[1, 1, 2, 3, 10, 8, 6]
[1, 1, 2, 3, 10, 8, 6]
原始数据：
[1, 1, 2, 3, 10, 8, 6]
原始数据：
[1, 1, 2, 3, 10, 8, 6]
原始数据：
[1, 1, 2, 3, 10, 8, 6]
[1, 1, 2, 3, 6, 8, 10]

3、选择排序（Selection Sort）

3.1、核心思想

选择排序(Selection-sort)是一种简单直观的排序算法。
它的工作原理：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

3.2、动图演示

在这里插入图片描述

3.3、代码

def selection_sort(arr):

    for i in range(len(arr)):
        print(arr)
        for j in range(i + 1, len(arr)):
            min_num = arr[i]
            if min_num > arr[j]:
                p = arr[j]
                arr[j] = arr[i]
                arr[i] = p
    # print(arr)


selection_sort([3, 2, 10, 2, 9, 6, 2])

[3, 2, 10, 2, 9, 6, 2]
[2, 3, 10, 2, 9, 6, 2]
[2, 2, 10, 3, 9, 6, 2]
[2, 2, 2, 10, 9, 6, 3]
[2, 2, 2, 3, 10, 9, 6]
[2, 2, 2, 3, 6, 10, 9]
[2, 2, 2, 3, 6, 9, 10]

4、插入排序（Insertion Sort）

4.1、核心思想

插入排序（Insertion-Sort）的算法描述是一种简单直观的排序算法。
它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

4.2、动图演示

在这里插入图片描述

4.3、代码

def insertion_sort(arr):

    for i in range(1, len(arr)):
        preIdx = i - 1
        current = arr[i]

        print("第" + str(i) + "次循环输入数据：\n" + str(arr))

        # 下方这个跳出循环的部分比较巧妙，两个条件，缺一不可
        while preIdx >= 0 and arr[preIdx] > current:
            arr[preIdx + 1] = arr[preIdx]
            preIdx -= 1

            print("中间过程========" + str(arr))
        arr[preIdx + 1] = current
        print("第" + str(i) + "次循环输出结果：\n" + str(arr))

    print("最终结果：\n" + str(arr))


insertion_sort([3, 1, 10, 7, 9, 6, 2])

结果：

第1次循环输入数据：
[3, 1, 10, 7, 9, 6, 2]
中间过程========[3, 3, 10, 7, 9, 6, 2]
第1次循环输出结果：
[1, 3, 10, 7, 9, 6, 2]
第2次循环输入数据：
[1, 3, 10, 7, 9, 6, 2]
第2次循环输出结果：
[1, 3, 10, 7, 9, 6, 2]
第3次循环输入数据：
[1, 3, 10, 7, 9, 6, 2]
中间过程========[1, 3, 10, 10, 9, 6, 2]
第3次循环输出结果：
[1, 3, 7, 10, 9, 6, 2]
第4次循环输入数据：
[1, 3, 7, 10, 9, 6, 2]
中间过程========[1, 3, 7, 10, 10, 6, 2]
第4次循环输出结果：
[1, 3, 7, 9, 10, 6, 2]
第5次循环输入数据：
[1, 3, 7, 9, 10, 6, 2]
中间过程========[1, 3, 7, 9, 10, 10, 2]
中间过程========[1, 3, 7, 9, 9, 10, 2]
中间过程========[1, 3, 7, 7, 9, 10, 2]
第5次循环输出结果：
[1, 3, 6, 7, 9, 10, 2]
第6次循环输入数据：
[1, 3, 6, 7, 9, 10, 2]
中间过程========[1, 3, 6, 7, 9, 10, 10]
中间过程========[1, 3, 6, 7, 9, 9, 10]
中间过程========[1, 3, 6, 7, 7, 9, 10]
中间过程========[1, 3, 6, 6, 7, 9, 10]
中间过程========[1, 3, 3, 6, 7, 9, 10]
第6次循环输出结果：
[1, 2, 3, 6, 7, 9, 10]
最终结果：
[1, 2, 3, 6, 7, 9, 10]

5、归并排序

5.1、思想

来源：归并排序（Merge Sort）图解，归并排序算法-学到牛牛
归并排序是建立在归并操作上的一种有效、稳定的排序算法，该算法采用非常经典的分治法（分治法可以通俗的解释为:把一片领土分解，分解为若干块小部分，然后一块块地占领征服，被分解的可以是不同的政治派别或是其他什么，然后让他们彼此异化），归并排序的思路很简单，速度呢，也仅此于快速排序

基本思路：

第一步：将序列中待排序数字分为若干组，每个数字分为一组。

第二步：将若干组两两合并，保证合并的组都是有序的。

第三步：重复第二步的操作，直到剩下最后一组即为有序数列。

详细步骤：

首先将数组中待排序数字分成若干组,每个数字为一组
在这里插入图片描述
相邻的两组进行对比，并且两两合并，保证合并后都是有序的数列，i（数字8）> j（数字4）需要交换位置（最终呈现一个升序的数组），经过比较合并后两个数存入一个空的指针里

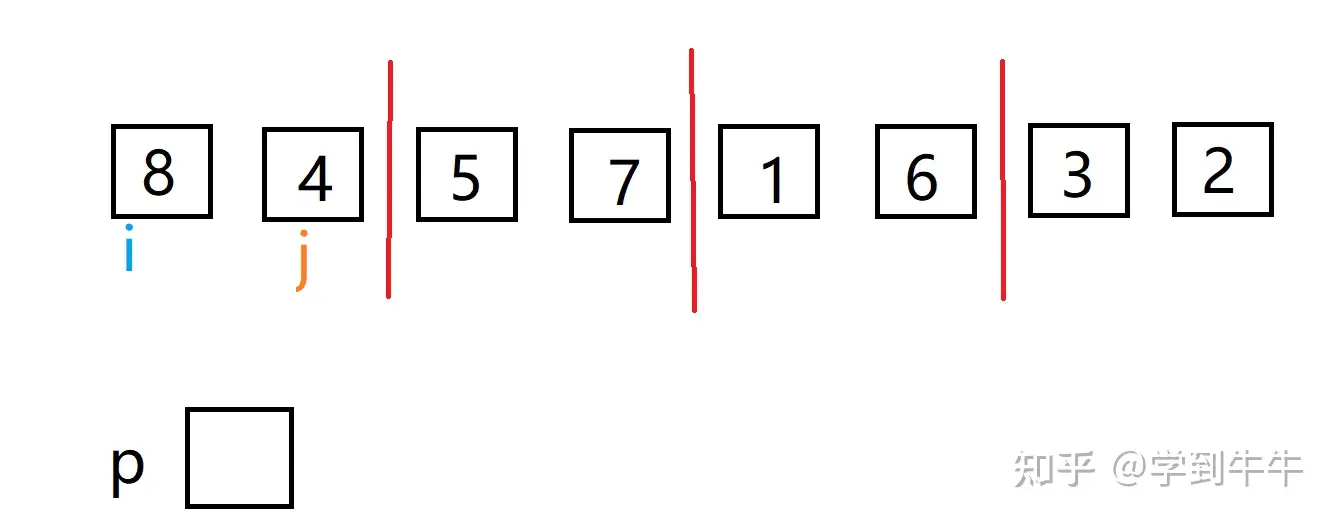
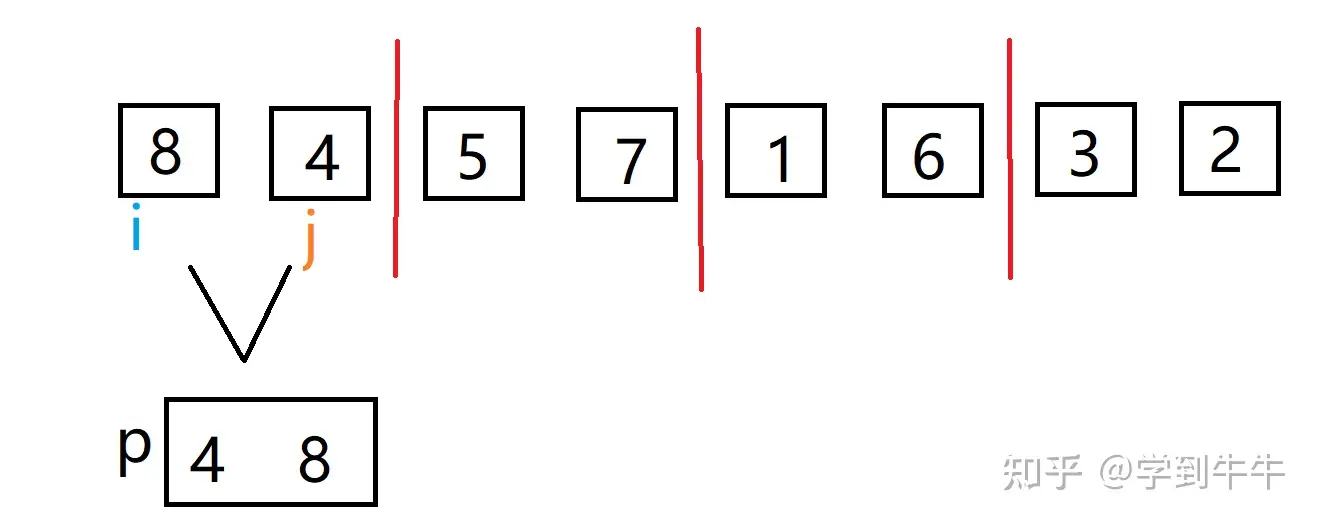
其他组按照此方法依次合并，从8个组合并成4个组
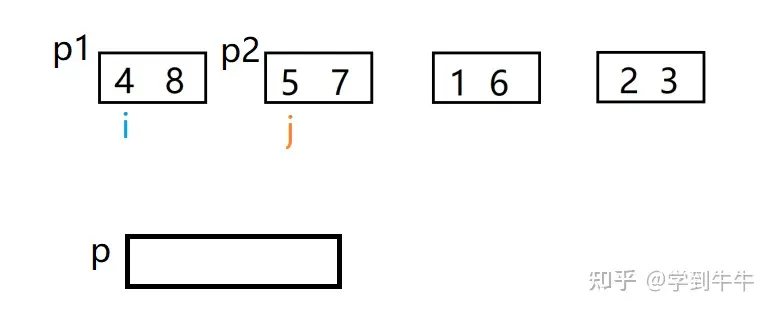
在这里插入图片描述
继续相邻的两个组进行合并

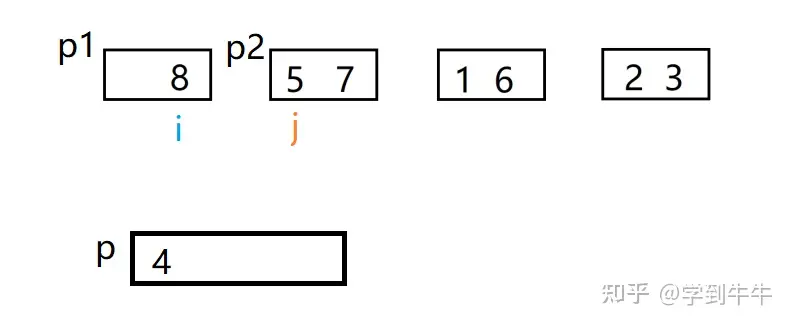
定义两个变量i,j分别代表P1里的第一个值（4）和P2里的第一个值（5），i和j进行比较，i < j（4 < 5）,将数字4移入p中，i向后移动一位

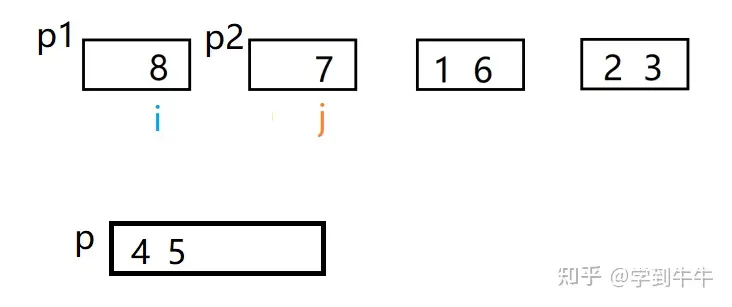
在这里插入图片描述
i和j进行比较，i > j（8 > 5 ）,将数字5移动到p中（4的后一位），j后移一位

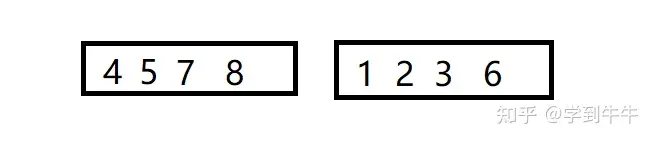
i 和j继续进行比较，i > j （8 > 7）,将数字7移动到p中（5的后一位），p2中没有待排序的数字，所以比较结束，p1中剩下的数字移动到p中（7的后一位），合并结束。旁边两个序列按照同样的方式进行合并，最后得到两个有序序列，将这两个有序序列通过上面的方式继续进行合并

在这里插入图片描述
i和j进行比较，i > j（4 > 1）,i不动，p2中的数字1移动到p中，j向后移动一位

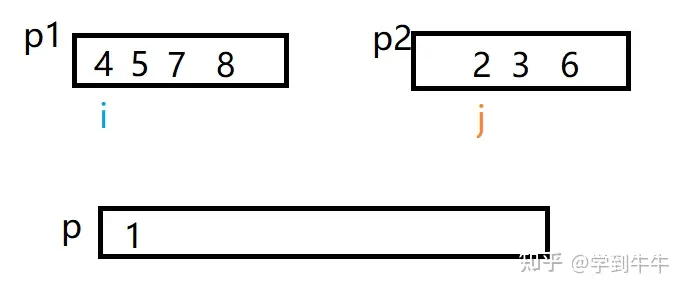
i继续和j比较，i > j（4 > 2）,数字2移动到p中（1的后一位），j向后移动一位

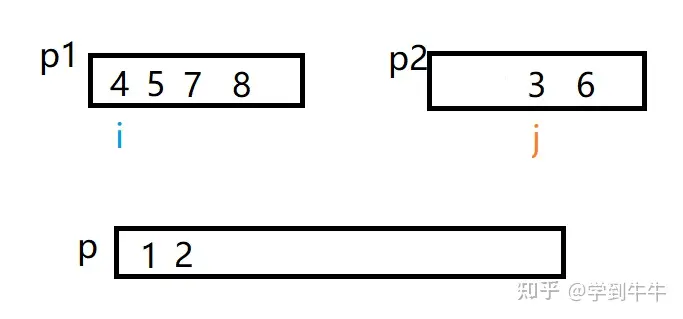
在这里插入图片描述
i继续和j比较，i > j（4 > 3）,数字3移动到p中（2的后一位），j向后移动一位

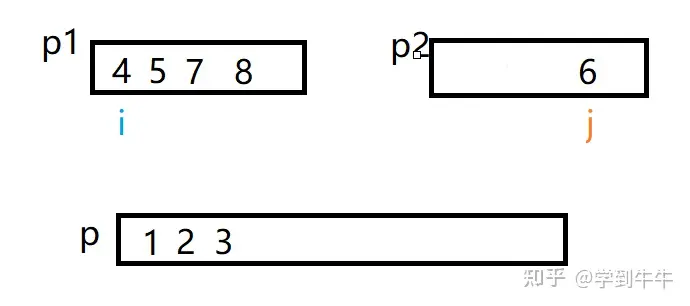
在这里插入图片描述
i继续和j比较，i < j（4 <6）,数字4移动到p中（3的后一位），i向后移动一位

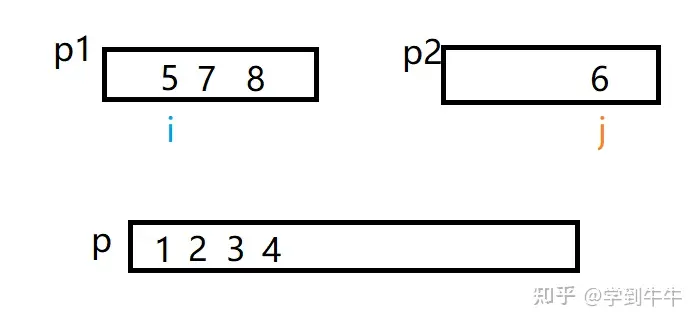
i继续和j比较，i > j（7 >6）,数字6移动到p中（5的后一位），p2中已经没有待排序的数字，所以比较结束，p1中剩下的数字移动到p中（6的后面）
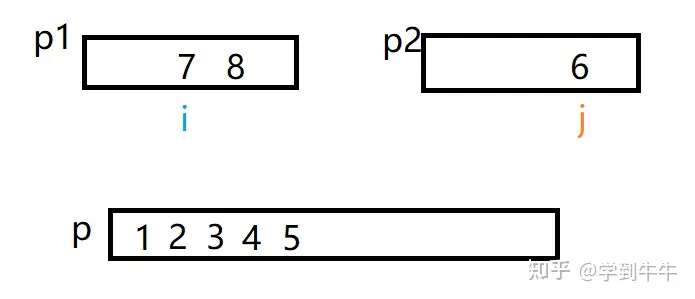
在这里插入图片描述
最后得到一个有序的数列，归并排序结束

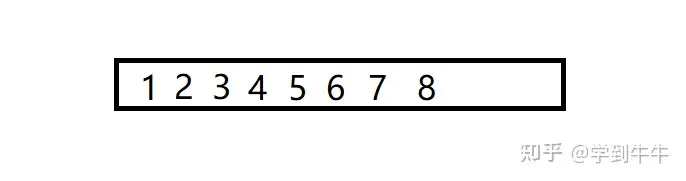
5.2、代码

def merge_sort(arr):
    # 判断是否需要继续划分  
    if len(arr) <= 1:
        return arr

    # 将数组划分为左右两部分
    mid = len(arr) // 2
    left = arr[:mid]
    right = arr[mid:]

    # 递归地对左右两部分进行排序  
    left = merge_sort(left)
    right = merge_sort(right)

    # 合并左右两部分  
    return merge(left, right)


def merge(left, right):
    result = []  # 存储合并后的结果  
    i = j = 0  # i和j分别指向左右两部分的起始位置  
    while i < len(left) and j < len(right):
        # 如果左部分当前元素小于等于右部分当前元素，则将其加入结果列表  
        if left[i] <= right[j]:
            result.append(left[i])
            i += 1
            # 否则将右部分当前元素加入结果列表
        else:
            result.append(right[j])
            j += 1
            # 如果左部分还有剩余元素，将其加入结果列表
    while i < len(left):
        result.append(left[i])
        i += 1
        # 如果右部分还有剩余元素，将其加入结果列表
    while j < len(right):
        result.append(right[j])
        j += 1
    return result


if __name__ == '__main__':
    print(merge_sort([3, 11, 6, 2, 5, 8]))

6、二分查找

def binary_search(arr, left, right, target):
    if left > right:
        return '-1'

    mind = (left + right) // 2

    if target > arr[mind]:
        left = mind + 1
    elif target < arr[mind]:
        right = mind - 1
    elif target == arr[mind]:
        return mind
    else:
        return "-1"

    return binary_search(arr, left, right, target)


ll = [1, 2, 3, 5, 6, 8]
print(binary_search(ll, 0, len(ll)-1, 5))

7、二叉树遍历

class TreeNode:
    def __init__(self, value = None, left = None, right = None):
        self.value = value
        self.left = left
        self.right = right


def preTraverse(root):
    if root == None:
        return None

    print(root.value)
    preTraverse(root.left)
    preTraverse(root.right)


def mindTraverse(root):
    if root == None:
        return None

    mindTraverse(root.left)
    print(root.value)
    mindTraverse(root.right)

def afterTraverse(root):
    if root == None:
        return None

    afterTraverse(root.left)
    afterTraverse(root.right)
    print(root.value)


root = TreeNode('A', TreeNode('D', TreeNode('ld'), TreeNode('rd')), TreeNode('E', TreeNode('le'), TreeNode('re')))

print("前序遍历：\n")
preTraverse(root)
print("中序遍历：\n")
mindTraverse(root)
print("后序遍历：\n")
afterTraverse(root)