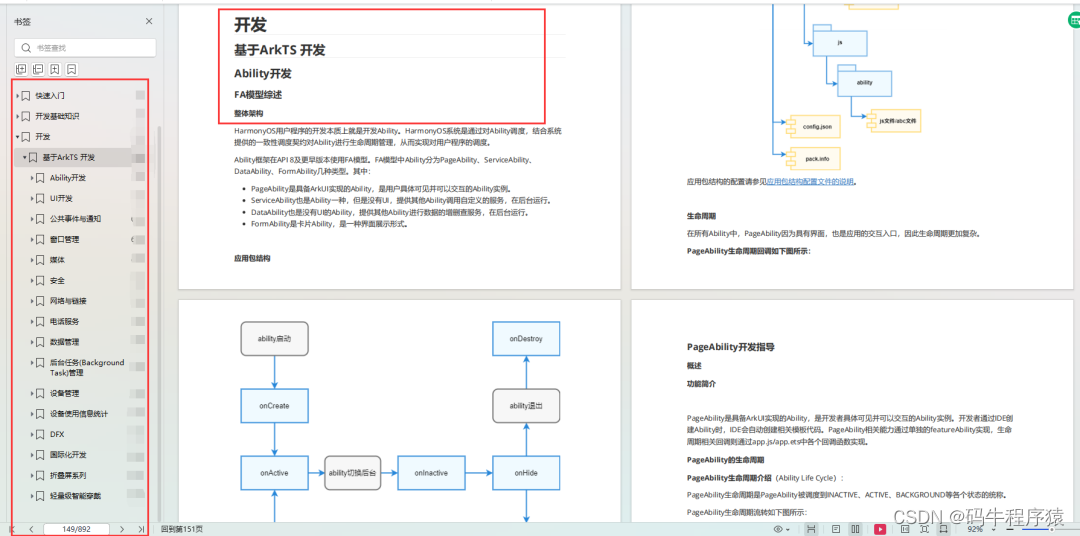
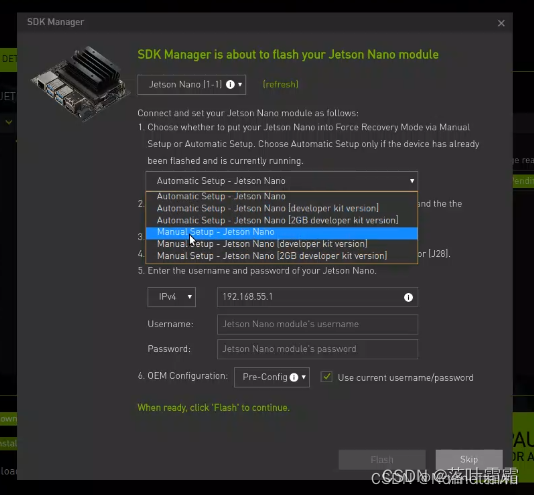
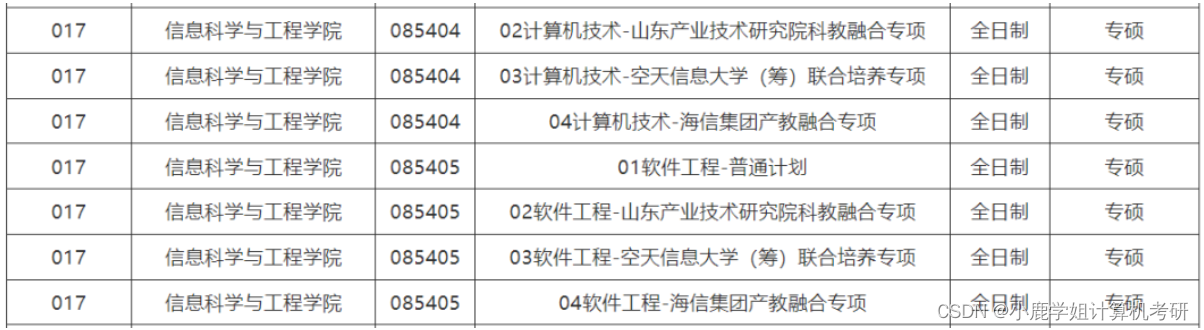
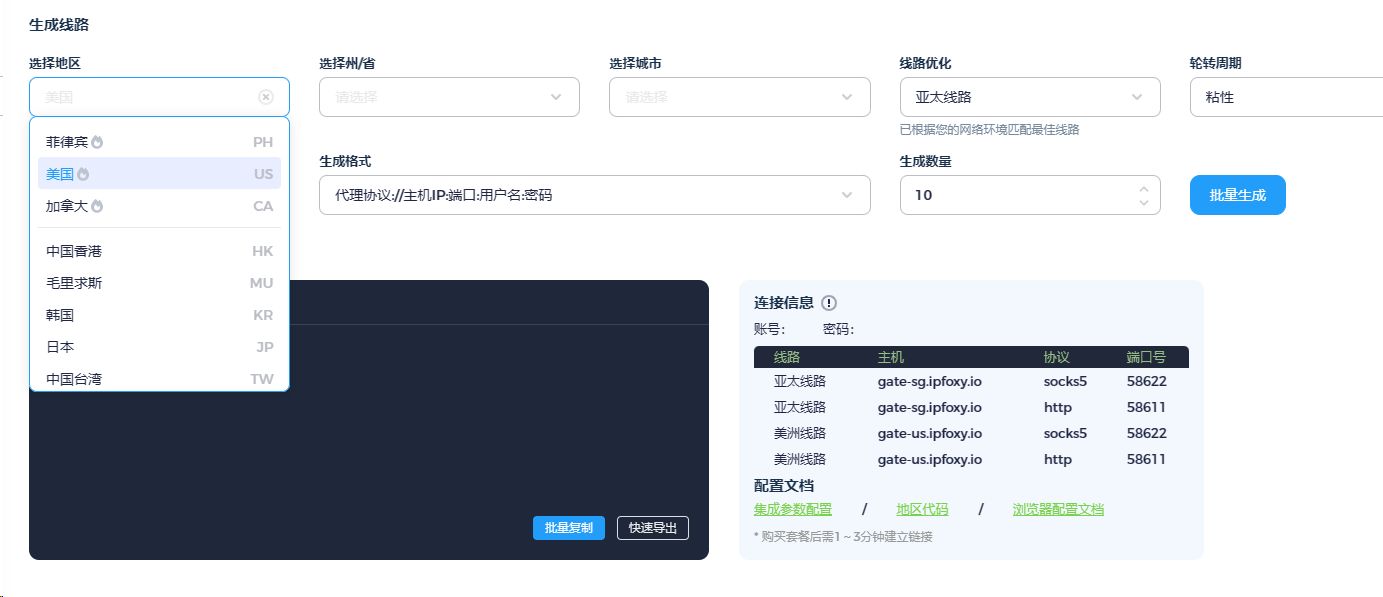
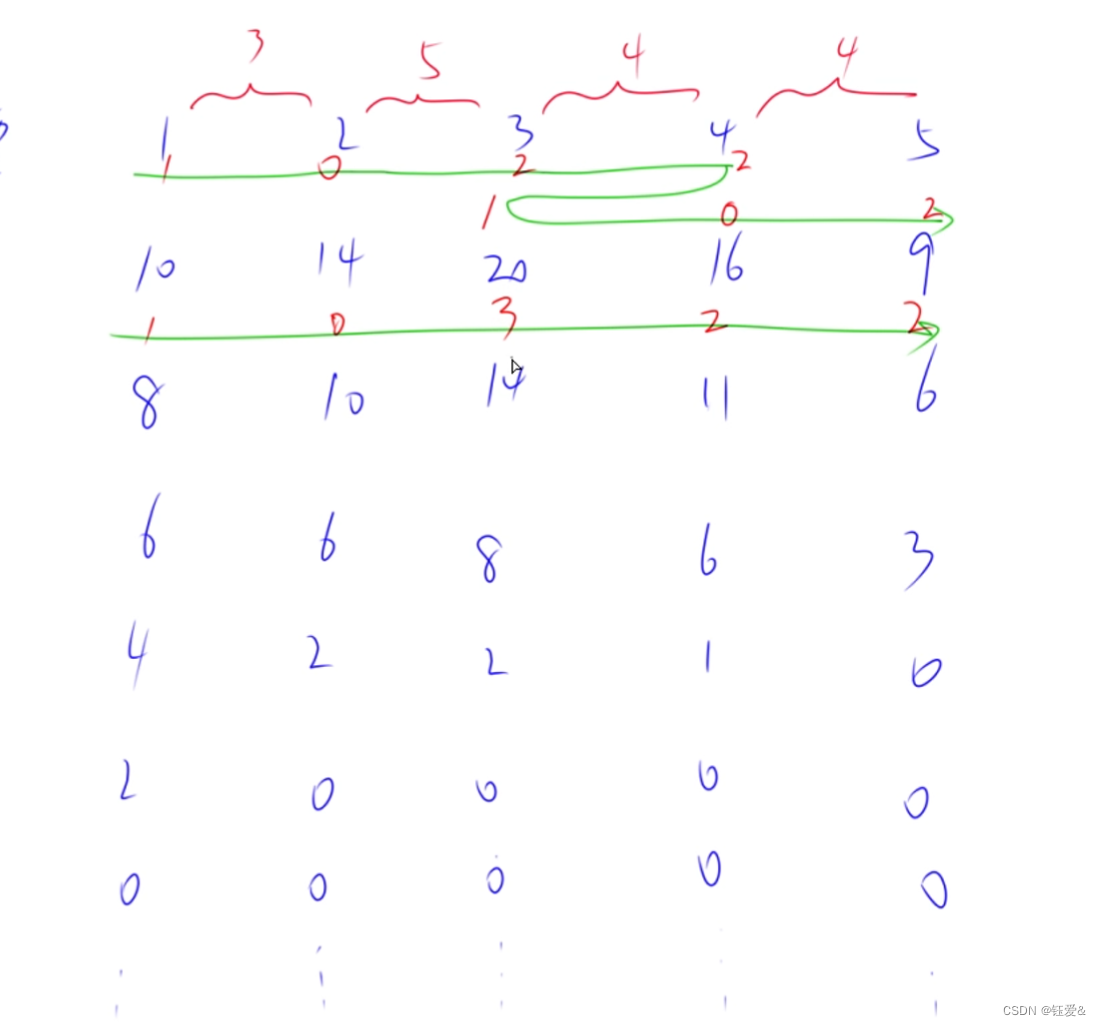
有 N 个鱼塘排成一排,每个鱼塘中有一定数量的鱼,例如:N=5 时,如下表:
| 鱼塘编号 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 第1分钟能钓到的鱼的数量(1..1000) | 10 | 14 | 20 | 16 | 9 |
| 每钓鱼1分钟钓鱼数的减少量(1..100) | 2 | 4 | 6 | 5 | 3 |
| 当前鱼塘到下一个相邻鱼塘需要的时间(单位:分钟) | 3 | 5 | 4 | 4 |
即:在第 11 个鱼塘中钓鱼第 11 分钟内可钓到 1010 条鱼,第 22 分钟内只能钓到 88 条鱼,……,第 55 分钟以后再也钓不到鱼了。
从第 11 个鱼塘到第 22 个鱼塘需要 33 分钟,从第 22 个鱼塘到第 33 个鱼塘需要 55 分钟,……
给出一个截止时间 T,设计一个钓鱼方案,从第 11 个鱼塘出发,希望能钓到最多的鱼。
假设能钓到鱼的数量仅和已钓鱼的次数有关,且每次钓鱼的时间都是整数分钟。
输入格式
共 55 行,分别表示:
第 11 行为 N;
第 22 行为第 11 分钟各个鱼塘能钓到的鱼的数量,每个数据之间用一空格隔开;
第 33 行为每过 11 分钟各个鱼塘钓鱼数的减少量,每个数据之间用一空格隔开;
第 44 行为当前鱼塘到下一个相邻鱼塘需要的时间;
第 55 行为截止时间 T。
输出格式
一个整数(不超过2e9-1),表示你的方案能钓到的最多的鱼。
数据范围
1≤N≤100
1≤T≤1000
输入样例:
5
10 14 20 16 9
2 4 6 5 3
3 5 4 4
14
输出样例:
76分析:
利用贪心思维,并不需要来回折返,如果钓完一分钟之后,这个鱼塘的鱼的数量依旧比其他鱼塘多,那就继续钓,这样可以节省来回的路上时间,使时间最大化
注意:
(1)int spend[N]={0};
(2)memset(spend,0,sizeof(spend));
两个的区别:
第一行:
这行代码是在定义数组时使用的,不是赋值操作,切记切记!!!
而且也只是给第一个数组赋值为0
第二行:
这个函数是C中的,作用是将spend数组全部赋值为0
#include<iostream>
#include<cstring>
using namespace std;
#define N 110
int fishnum[N],d[N],dtime[N],spend[N];//鱼数,减少量,下个鱼塘时间,钓鱼所花时间
int get(int k){//求出鱼的数量
return max(0,fishnum[k]-d[k]*spend[k]);
}
int work(int n,int T){
int res=0;
memset(spend,0,sizeof(spend));//将spend数组全部赋值为0
for(int i=0;i<T;i++){
int t=1;
for(int j=2;j<=n;j++){//从第二个开始枚举鱼塘
if(get(t)<get(j)){
t=j;
}
}
res+=get(t);//得到鱼的总数量
spend[t]++;
}
return res;
}
int main(){
int n,T;
cin>>n;
for(int i=1;i<=n;i++) cin>>fishnum[i];
for(int i=1;i<=n;i++) cin>>d[i];
for(int i=2;i<=n;i++){
cin>>dtime[i];
dtime[i]+=dtime[i-1];//前缀和
}
cin>>T;
int res=0;
for(int i=1;i<=n;i++){
res=max(res,work(i,T-dtime[i]));
}
cout<<res<<endl;
return 0;
}