目录
- 1.背景
- 2.算法原理
- 2.1算法思想
- 2.2算法过程
- 3.代码实现
- 4.参考文献
1.背景
2020年,Afshin Faramarzi等人受到估计动态和平衡状态的控制体积质量平衡模型启发,提出了平衡优化器(Equilibrium Optimizer, EO)。(PS:酒桶摇摇晃晃~)
2.算法原理
2.1算法思想

EO基于质量平衡方程,描述为一阶微分方程:
V
d
C
d
t
=
Q
C
e
q
−
Q
C
+
G
(1)
V\frac{dC}{dt}=QC_{eq}-QC+G \tag{1}
VdtdC=QCeq−QC+G(1)
其中,V 为容器的容积,C 为溶液密度,Q 为容量流率,Ceq 表示平衡状态下的浓度,G 为容器内的质量生成速率。
求解可以得到方程的解为:
C
=
C
e
q
+
(
C
0
−
C
e
q
)
F
+
G
λ
V
(
1
−
F
)
F
=
exp
[
−
λ
(
t
−
t
0
)
]
(2)
C=C_{eq}+\left(C_{0}-C_{eq}\right)F+\frac{G}{\lambda V}(1-\mathrm{F})\\ F=\exp\left[-\lambda\left(t-t_0\right)\right] \tag{2}
C=Ceq+(C0−Ceq)F+λVG(1−F)F=exp[−λ(t−t0)](2)
2.2算法过程
EO基于等式(2)进行更新,具体而言,C代表新解,C0代表旧解,Ceq代表当前最优解。
平衡池:
EO是领导者-跟随者类型算法, 这里采用排名前4个体进行引导,避免陷入局部解:
C
⃗
e
q
,
p
o
o
l
=
{
C
⃗
e
q
(
1
)
,
C
⃗
e
q
(
2
)
,
C
⃗
e
q
(
3
)
,
C
⃗
e
q
(
4
)
,
C
⃗
e
q
(
a
v
e
)
}
(3)
\vec C_{eq,pool}=\left\{\vec C_{eq(1)},\vec C_{eq(2)},\vec C_{eq(3)},\vec C_{eq(4)},\vec C_{eq(ave)}\right\}\tag{3}
Ceq,pool={Ceq(1),Ceq(2),Ceq(3),Ceq(4),Ceq(ave)}(3)
其中,
C
⃗
e
q
(
a
v
e
)
\vec C_{eq(ave)}
Ceq(ave)为4个体平均值,五者以等概率选择(0.2)。
系数F:
EO为了平衡全局探索与局部开发,对等式(2)中的F进行修正:
F
⃗
=
a
1
s
i
g
n
(
r
⃗
−
0.5
)
[
e
−
λ
⃗
t
−
1
]
(4)
\vec{F}=a_1sign\left(\vec{r}-0.5\right)\left[e^{-\vec{\lambda}t}-1\right] \tag{4}
F=a1sign(r−0.5)[e−λt−1](4)
质量生成速率G:
参数G控制局部开发收敛性:
G
⃗
=
G
⃗
0
e
−
λ
⃗
(
t
−
t
0
)
=
G
⃗
0
F
⃗
\vec{G}=\vec{G}_0e^{-\vec{\lambda}(t-t_0)}=\vec{G}_0\vec{F}
G=G0e−λ(t−t0)=G0F
G
0
→
=
G
C
P
→
(
C
e
q
→
−
λ
⃗
C
⃗
)
G
C
P
→
=
{
0.5
r
1
r
2
≥
G
P
0
r
2
<
G
P
(5)
\overrightarrow{G_0}=\overrightarrow{GCP}\left(\overrightarrow{C_{eq}}-\vec{\lambda}\vec{C}\right)\\\overrightarrow{GCP}=\begin{cases}0.5r_1&r_2\geq GP\\\\0&r_2<GP\end{cases}\tag{5}
G0=GCP(Ceq−λC)GCP=⎩
⎨
⎧0.5r10r2≥GPr2<GP(5)
位置更新:
C
⃗
=
C
⃗
e
q
+
(
C
⃗
−
C
⃗
e
q
)
.
F
⃗
+
G
⃗
λ
V
⃗
(
1
−
F
⃗
)
(6)
\vec{C}=\vec{C}_{eq}+\left(\vec{C}-\vec{C}_{eq}\right).\vec{F}+\frac{\vec{G}}{\vec{\lambda V}}\big(1-\vec{F}\big)\tag{6}
C=Ceq+(C−Ceq).F+λVG(1−F)(6)

伪代码:

3.代码实现
公众号:小O的算法实验室,免费获取
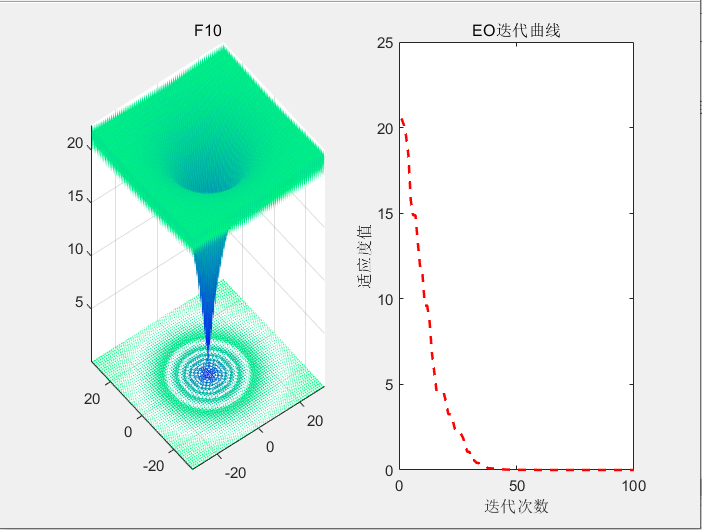
4.参考文献
[1] Faramarzi A, Heidarinejad M, Stephens B, et al. Equilibrium optimizer: A novel optimization algorithm[J]. Knowledge-based systems, 2020, 191: 105190.