备战2024年蓝桥杯 -- 每日一题
Python大学A组
试题一:有序分数
试题二:正则问题
试题三:带分数
试题四:约数之和
试题五:分形之城
试题一:有序分数
【题目描述】

【输入格式】
共一行,包含一个整数 N。
【输出格式】
按照从小到大的顺序,输出所有满足条件的分数。
每个分数占一行,格式为 a/b,其中 a为分子, b 为分母。
【数据范围】
1≤N≤160
【输入样例】
5【输出样例】
0/1
1/5
1/4
1/3
2/5
1/2
3/5
2/3
3/4
4/5
1/1【解题思路】
可以采取最简单直接的方法,直接枚举出所有分数,需要用到gcd(a,b)进行约分。然后去重接着排序即可。
【Python程序代码】
from math import *
n = int(input())
tep = set()
for i in range(1,n+1):
for j in range(1,i+1):
k = gcd(i,j)
ii,jj = i//k,j//k
tep.add( (jj/ii,jj,ii) )
tep = list(tep)
tep.sort()
print('0/1')
for i in range(len(tep)):
print( '%d/%d'%(tep[i][1],tep[i][2]) )
试题二:正则问题
【题目描述】
考虑一种简单的正则表达式:只由 x ( ) | 组成的正则表达式。小明想求出这个正则表达式能接受的最长字符串的长度。例如 ((xx|xxx)x|(x|xx))xx 能接受的最长字符串是: xxxxxx,长度是6。
【输入格式】
一个由x()|组成的正则表达式。
【输出格式】
输出所给正则表达式能接受的最长字符串的长度。
【数据范围】
输入长度不超过100,保证合法。
【输入样例】
((xx|xxx)x|(x|xx))xx 【输出样例】
6【解题思路】
采用递归回溯的方法,首先建立两条规则:
规则1:() 的意思是有括号的先算括号里面的,优先级最高,把括号计算的结果在和括号外的字符拼接,即括号是相对独立,完整的个体
规则2:|的意思是|这个符号两侧的字符串只能选其中一个,由于这题要求能拼接的字符串最长,因此应该选择字符|字符串xxx...长度较大的一侧
比如样例中的字符串((xx|xxx)x|(x|xx))xx对应的递归搜索树如下:
【Python程序代码】
s = input()
k = 0
def dfs():
global k
res = 0
while k<len(s):
if s[k]=='(':
k += 1
res += dfs()
k += 1
elif s[k]=='|':
k += 1
res = max(res, dfs())
elif s[k]==')':
break
elif s[k]=='x':
k += 1
res += 1
else:break
return res
print(dfs())试题三:带分数
【题目描述】

【输入格式】
一个正整数。
【输出格式】
输出输入数字用数码 1∼9不重复不遗漏地组成带分数表示的全部种数。
【数据范围】
1≤N<1000000
【输入样例】
100【输出样例】
11【解题思路】
可以考虑采用Python的permuttations的Api函数,然后枚举两个隔板将排列切分成三个数后进行判断。可以再采取一定的剪枝加速。
【Python程序代码】
from itertools import *
x = int(input())
a = ['1','2','3','4','5','6','7','8','9']
res = 0
for pl in permutations(a,9):
tep = list(pl)
tep = "".join(tep)
for i in range(1,8):
if int(tep[:i])>=x:break
for j in range(i+1,9):
a1 = int(tep[:i])
a2 = int(tep[i:j])
a3 = int(tep[j:])
if a2%a3==0 and a2//a3==x-a1:res+=1
print(res)试题四:约数之和
【题目描述】

【输入格式】
在一行中输入用空格隔开的两个整数 A 和 B。
【输出格式】
输出一个整数,代表 S mod 9901的值。
【数据范围】
0≤A,B≤5×10000000
【输入样例】
2 3【输出样例】
15【解题思路】
首先得明确这题到底需要干什么:
【Python程序代码】
a,b = map(int,input().split())
res = 1
mod = 9901
def summ(p,k):
if k==1:return 1
elif k%2==0:return (pow(p,k//2,mod) + 1)*(summ(p,k//2))%mod
else:return ( summ(p,k-1) + pow(p,k-1,mod) )%mod
i = 2
while i*i<=a:
if a%i==0:
c = 0
while a%i==0:
c += 1
a//=i
res = res*( summ(i,c*b+1) )%mod
i += 1
if a>1:
res = res * (summ(a, b+1)) % mod
elif a==0:
res = 0
print(res)
试题五:分形之城
【题目描述】
城市的规划在城市建设中是个大问题。不幸的是,很多城市在开始建设的时候并没有很好的规划,城市规模扩大之后规划不合理的问题就开始显现。而这座名为 Fractal 的城市设想了这样的一个规划方案,如下图所示:
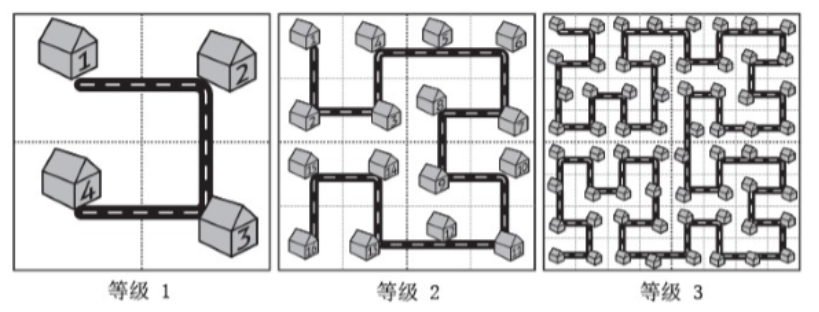
当城区规模扩大之后,Fractal 的解决方案是把和原来城区结构一样的区域按照图中的方式建设在城市周围,提升城市的等级。对于任意等级的城市,我们把正方形街区从左上角开始按照道路标号。虽然这个方案很烂,Fractal 规划部门的人员还是想知道,如果城市发展到了等级 N,编号为 A 和 B的两个街区的直线距离是多少。街区的距离指的是街区的中心点之间的距离,每个街区都是边长为 10米的正方形。
【输入格式】
第一行输入正整数 n,表示测试数据的数目。
以下 n行,输入 n组测试数据,每组一行。
每组数据包括三个整数 N,A,B表示城市等级以及两个街区的编号,整数之间用空格隔开。
【输出格式】
一共输出 n行数据,每行对应一组测试数据的输出结果,结果四舍五入到整数。
【数据范围】
1≤N≤31,
1≤A,B≤2^(2n),
1≤n≤1000
【输入样例】
3
1 1 2
2 16 1
3 4 33 【输出样例】
10
30
50 【解题思路】
具体思路参考:思路
数学知识:
- 对于点 (x, y) ,沿原点顺时针旋转 90° ,将变为 (y, -x)
- 对于点 (x, y) ,沿原点逆时针旋转 90° ,将变为 (-y, x)
- 对于点 (x, y) ,以 y 轴为对称轴翻转将变为 (-x, y)
【Python程序代码】
from math import *
n = int(input())
def calc(n,m):
if n==0:return [0,0]
le = 1 << (n-1)
cnt = 1<< (2*n-2)
pos = calc(n-1, m%cnt)
x,y = pos
z = m//cnt
if z==0:return [-y-le,-x+le]
elif z==1:return [x+le,y+le]
elif z==2:return [x+le,y-le]
return [y-le,x-le]
def work(x,y):
return (5*((x[0]-y[0])**2 + (x[1]-y[1])**2)**0.5)
for i in range(n):
n,a,b = map(int,input().split())
pos1 = calc(n,a-1)
pos2 = calc(n,b-1)
print(round(work(pos1,pos2)))