问题描述:
小蓝有一个保险箱,保险箱上共有 n 位数字。小蓝可以任意调整保险箱上的每个数字,每一次操作可以将其中一位增加 1 或减少 1。当某位原本为 9 或 0 时可能会向前(左边)进位/退位,当最高位(左边第一位)上的数字变化时向前的进位或退位忽略。
例如:
00000 的第 5 位减 1 变为 99999;
99999 的第 5 位减 1 变为 99998;
00000的第 4 位减 1 变为 99990;
97993 的第 4 位加 1 变为 98003;
99909 的第 3 位加 1 变为 00009。
保险箱上一开始有一个数字 x,小蓝希望把它变成 y,这样才能打开它,问小蓝最少需要操作的次数。
输入格式
输入的第一行包含一个整数 n。第二行包含一个 n 位整数 x。第三行包含一个 n 位整数 y。
输出格式
输出一行包含一个整数表示答案。
数据范围
对于 30% 的评测用例,1≤n≤300;
对于 60% 的评测用例,1≤n≤3000;
对于所有评测用例,1≤n≤105,x,y 中仅包含数字 0 至 9,可能有前导零。
输入样例:
5
12349
54321
输出样例:
11
思路:
又是一道省赛且没有完全AC的题,这道题刚开始压根没往动态规划方面想,结果是一个二维dp数组,其中一维表示3种状态,未进位,进位和退位状态。
下面进行分析:
分析题目发现每变动一位数字,只会影响左边的一个数。如果此时该位的数没有发生进位的话,左边的一个数就不会发生变动的;如果当前该位的数是通过加法进位的话,那么左边的一位数字就会加1;如果当前该位的数是通过减法进位的话,那么左边的一位数字就会减1。
所以发现当前一位数字是否发生变动是取决于后一位数字的变动,所以定义三种状态:
- 右边的数字没有发生进位
- 右边数字通过加法发生了进位
- 右边的数字通过减法发生了进位。
动规五部曲:
- 定义dp数组:
dp[i][0],dp[i][1],dp[i][2] 分别表示当前位没有发生进位、当前位通过加法发生进位和当前位通过减法发生进位需要操作的最少次数。
- 递推公式:
接下来关键之处就是状态计算了,由于操作当前位并不影响右边的数,所以从右向左进行状态计算(用x表示第一个字符串当前位的数字,用y表示第二个字符串当前位的数字):
-
当前位的数没有发生进位dp[i][0]
1)如果右边的数操作完了之后当前位没有发生改变,那么:
当前位不进位需要操作的次数即为:dp[i][0] = dp[i + 1][0] + abs(x - y)
2)如果右边的数操作完了之后当前位增大了一位,那么:
当前位不进位需要操作的次数即为:dp[i][0] = dp[i + 1][1] + abs(x + 1 - y)
因为发生了进位,所以x要加13)如果右边的数操作完了之后当前位减小了一位,那么:
当前位不进位需要操作的次数即为:dp[i][0] = dp[i + 1][2] + abs(x - 1 - y)
因为发生了退位,所以x要减1综上:dp[i][0] = min(dp[i + 1][0] + abs(x - y),dp[i + 1][1] + abs(x + 1 - y), dp[i + 1][2] + abs(x - 1 - y))
-
当前位的数通过加法进位dp[i][1]
1)如果右边的数操作完了之后当前位没有发生改变,那么:
当前位通过加法进位需要操作的次数即为:dp[i][1] = dp[i + 1][0] + abs(10 - (x - y))
如果x为2,y为8,则发生进位的情况是abs(10 -(2 - 8)) = 16,2进位到8需要加162)如果右边的数操作完了之后当前位增大了一位,那么:
当前位通过加法进位需要操作的次数即为:dp[i][1] = dp[i + 1][1] + abs(10 - (x + 1 - y))
3)如果右边的数操作完了之后当前位减小了一位,那么:
当前位通过加法进位需要操作的次数即为:dp[i][1] = dp[i + 1][2] + abs(10 - (x - 1 - y))
综上:dp[i][1] = min(dp[i + 1][0] + abs(10 - (x - y)),dp[i + 1][1] + abs(10 - (x + 1 - y)), dp[i + 1][2] + abs(10 - (x - 1 - y)))
-
当前位的数通过减法进位
1)如果右边的数操作完了之后当前位没有发生改变,那么:
当前位通过减法进位需要操作的次数即为:dp[i][2] = dp[i + 1][0] + abs(10 + (x - y))
如果x为2,y为8,则发生退位的情况是abs(10 +(2 - 8)) = 4,2退位到8需要减42)如果右边的数操作完了之后当前位增大了一位,那么:
当前位通过减法进位需要操作的次数即为:dp[i][2] = dp[i + 1][1] + abs(10 + (x + 1 - y))
3)如果右边的数操作完了之后当前位减小了一位,那么:
当前位通过减法进位需要操作的次数即为:dp[i][2] = dp[i + 1][2] + abs(10 + (x - 1 - y))
综上:dp[i][2] = min(dp[i + 1][0] + abs(10 + (x - y)),dp[i + 1][1] + abs(10 + (x + 1 - y)), dp[i + 1][2] + abs(10 + (x - 1 - y)))
- dp数组如何初始化:
因为递推公式是从右往左计算,所以
# 初始化最后一个位置的 dp 值
dp[n - 1][0] = abs(a[n - 1] - b[n - 1])
dp[n - 1][1] = abs(10 - (a[n - 1] - b[n - 1]))
dp[n - 1][2] = abs(10 + (a[n - 1] - b[n - 1]))
- dp数组遍历顺序:
因为递推公式是从右往左计算,所以从右往左遍历
# 从倒数第二个位置开始向前遍历
for i in range(n - 2, -1, -1):
- 打印dp数组:
999 变到 321
上方表示状态
左侧表示数的索引值
如图:
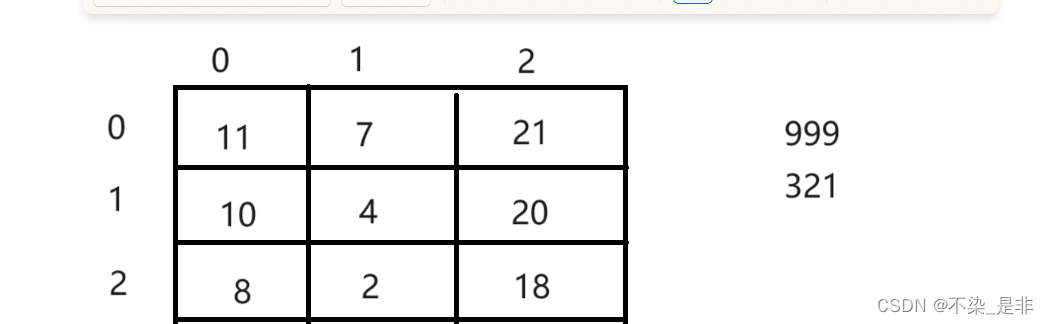
最终答案为min(dp[0][0], dp[0][1], dp[0][2])
代码及详细注释:
# 读取输入的整数 n,表示数组的长度
n = int(input())
# 读取输入的两个整数列表 a 和 b,分别表示两个数组
a = list(map(int, input())) # 将输入的字符串映射为整数列表
b = list(map(int, input())) # 将输入的字符串映射为整数列表
# dp[i][j] 表示到达位置 i 时,使得 a[i] 的数字与 b[i] 的数字相等的最小操作次数,
# 其中 j 可能取值为 0、1、2,分别表示 a[i] - b[i] 等于 0、1、-1。
dp = [[0, 0, 0] for _ in range(n)]
# 初始化最后一个位置的 dp 值
dp[n - 1][0] = abs(a[n - 1] - b[n - 1])
dp[n - 1][1] = abs(10 - (a[n - 1] - b[n - 1]))
dp[n - 1][2] = abs(10 + (a[n - 1] - b[n - 1]))
# 从倒数第二个位置开始向前遍历
for i in range(n - 2, -1, -1):
x = a[i]
y = b[i]
# 计算当前位置的 dp 值
dp[i][0] = dp[i + 1][0] + abs(x - y)
dp[i][0] = min(dp[i][0], dp[i + 1][1] + abs(x + 1 - y))
dp[i][0] = min(dp[i][0], dp[i + 1][2] + abs(x - 1 - y))
dp[i][1] = dp[i + 1][0] + abs(10 - (x - y))
dp[i][1] = min(dp[i][1], dp[i + 1][1] + abs(10 - (x + 1 - y)))
dp[i][1] = min(dp[i][1], dp[i + 1][2] + abs(10 - (x - 1 - y)))
dp[i][2] = dp[i + 1][0] + abs(10 + (x - y))
dp[i][2] = min(dp[i][2], dp[i + 1][1] + abs(10 + (x + 1 - y)))
dp[i][2] = min(dp[i][2], dp[i + 1][2] + abs(10 + (x - 1 - y)))
# 输出最小操作次数
print(min(dp[0][0], dp[0][1], dp[0][2]))
总结:
省赛10分的题,结果写了半天ac了25%,拿了3分,之后看到类似的题分析到状态就要考虑是否能用dp来解决。