一.题目原型



二.思路解析
1.动态规划
这道题要求的是矩阵的最大移动次数。根据题目意思,从索引 0 列开始向右移动,每次移动一列,最多移动到 n - 1 列,也就是 n - 1次。其移动规则为:当前单元格可以移动到其右上方、正右方以及右下方三个位置中严格大于其的单元格。那么换个角度想,一个单元格可以从其左上方、正左方以及左下方的单元格转移过来。
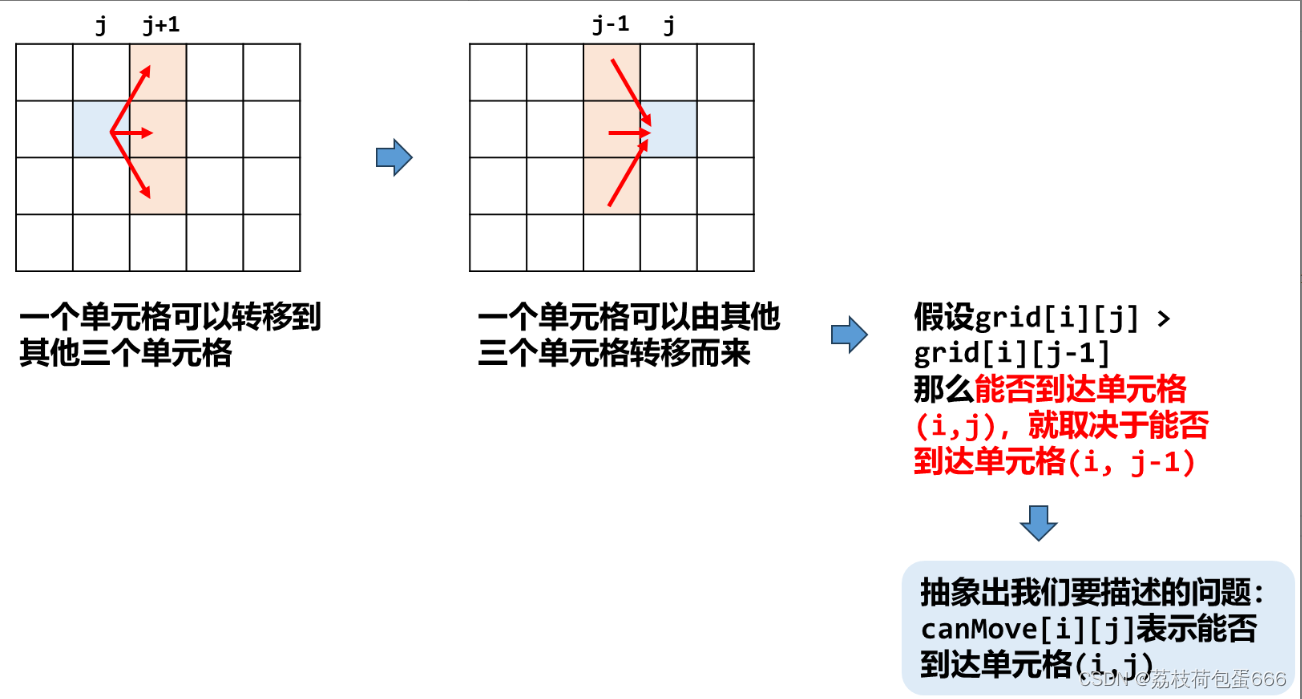
这不就是我们动态规划最开始的典型思路吗?
在这题中,我们从第一列开始,往后能走多少,到了第几列,其实就是这一次的走的步数,走到最远的列,就是最大的移动次数。
我们创建一个二维dp数组,初始化为0,我们从不同行的第一列元素开始走,能走到的地方我们做一个标记为1,已经标记过的我们就不再去走了,以免死循环。
int m=grid.size(),n=grid[0].size(),max_j=0;
vector<vector<int>>dp(m,vector<int>(n,0));
for(int i=0;i<m;++i){//初始化
dp[i][0]=1;
}dp【i】【j】由dp【i-1】【j-1】和dp【i】【j-1】和dp【i+1】【j】决定
for(int j=1;j<n;++j){//从第1列开始
for(int i=0;i<m;++i){
if((dp[i][j-1]==1&&grid[i][j]>grid[i][j-1])||(i-1>-1&&dp[i-1][j-1]==1&&grid[i][j]>grid[i-1][j-1])||(i+1<m&&dp[i+1][j-1]==1&&grid[i][j]>grid[i+1][j-1])){
dp[i][j]=1;
max_j=j;
}
}
}2.深度优先遍历
从第一列的任一单元格 (i,0)开始递归。枚举往右上/右/右下三个方向走,如果走一步后,没有出界,且格子值大于 grid[i][j],则可以走,继续递归。
在递归过程中,记录能访问到的最大列号,作为答案。
代码实现时,为避免重复递归之前访问过的格子,可以用一个 vis 数组标记访问过的格子。但实际上,可以把 grid[i][j]置为 0从而无需创建 vis数组。这是因为网格值均为正数,并且我们只能访问到比当前格子值更大的格子,所以置为 0 会导致永远无法访问到该格子,这正是我们所希望的。grid[i][j]置为0,表示这个点我们已经走过了,之后没有必要再走了,因为再往这个点走,移动的次数都是一样的。标记后就肯定不会再走了,因为要往后走的一个条件就是后面的点的值大于当前点的值。
function<void(int, int)> dfs = [&](int i, int j) {
ans = max(ans, j);
if (ans == n - 1) { // ans 已达到最大值
return;
}
// 向右上/右/右下走一步
for (int k = max(i - 1, 0); k < min(i + 2, m); k++) {
if (grid[k][j + 1] > grid[i][j]) {
dfs(k, j + 1);
}
}
grid[i][j] = 0;
};3.广度优先遍历
同样,我们也可以使用BFS的方法,我们首先将所有的行坐标加入集合中,表示这些地方都可以走,作为出发点。然后依次进行遍历,找到下一列可以走到的所有行坐标,这些下一列的行坐标都是严格满足比其走过来的点值要大的,然后将这些行坐标的集合替换掉之前的集合,再进行遍历,找到下一列能够走到的行坐标。直到没有能走的行坐标,或者走到最后一列为止。
我们需要一个vis数组去标记走过的位置,不能再走了
定义一个判断坐标合法的函数is_valid去判断坐标是不是合法的。
三.代码实现:
动态规划(DP)
class Solution {
public:
int maxMoves(vector<vector<int>>& grid) {
int m=grid.size(),n=grid[0].size(),max_j=0;
vector<vector<int>>dp(m,vector<int>(n,0));
for(int i=0;i<m;++i){//初始化
dp[i][0]=1;
}
for(int j=1;j<n;++j){//从第1列开始
for(int i=0;i<m;++i){
if((dp[i][j-1]==1&&grid[i][j]>grid[i][j-1])||(i-1>-1&&dp[i-1][j-1]==1&&grid[i][j]>grid[i-1][j-1])||(i+1<m&&dp[i+1][j-1]==1&&grid[i][j]>grid[i+1][j-1])){
dp[i][j]=1;
max_j=j;
}
}
}
return max_j;
}
};
深度优先遍历(DFS)
class Solution {
public:
int maxMoves(vector<vector<int>> &grid) {
int m = grid.size(), n = grid[0].size();
int ans = 0;
function<void(int, int)> dfs = [&](int i, int j) {
ans = max(ans, j);
if (ans == n - 1) { // ans 已达到最大值
return;
}
// 向右上/右/右下走一步
for (int k = max(i - 1, 0); k < min(i + 2, m); k++) {
if (grid[k][j + 1] > grid[i][j]) {
dfs(k, j + 1);
}
}
grid[i][j] = 0;
};
for (int i = 0; i < m; i++) {
dfs(i, 0); // 从第一列的任一单元格出发
}
return ans;
}
};
广度优先遍历(BFS)
class Solution {
public:
int maxMoves(vector<vector<int>>& grid) {
int M = grid.size(), N = grid[0].size();
auto is_valid = [&](int r, int c) -> bool {
return 0 <= r && r < M && 0 <= c && c < N;
};
queue<pair<int, int>> que;
vector<vector<bool>> vis(M, vector<bool>(N, false));
for (int r = 0; r < M; r++) {
vis[r][0] = true;
que.push(make_pair(r, 0));
}
int ans = 0;
while (!que.empty()) {
auto [r, c] = que.front(); que.pop();
ans = max(ans, c);
int ce = c+1;
for (const int& re : {r-1, r, r+1}) {
if (is_valid(re, ce) && !vis[re][ce] && grid[r][c] < grid[re][ce]) {
vis[re][ce] = true;
que.push(make_pair(re, ce));
}
}
}
return ans;
}
};