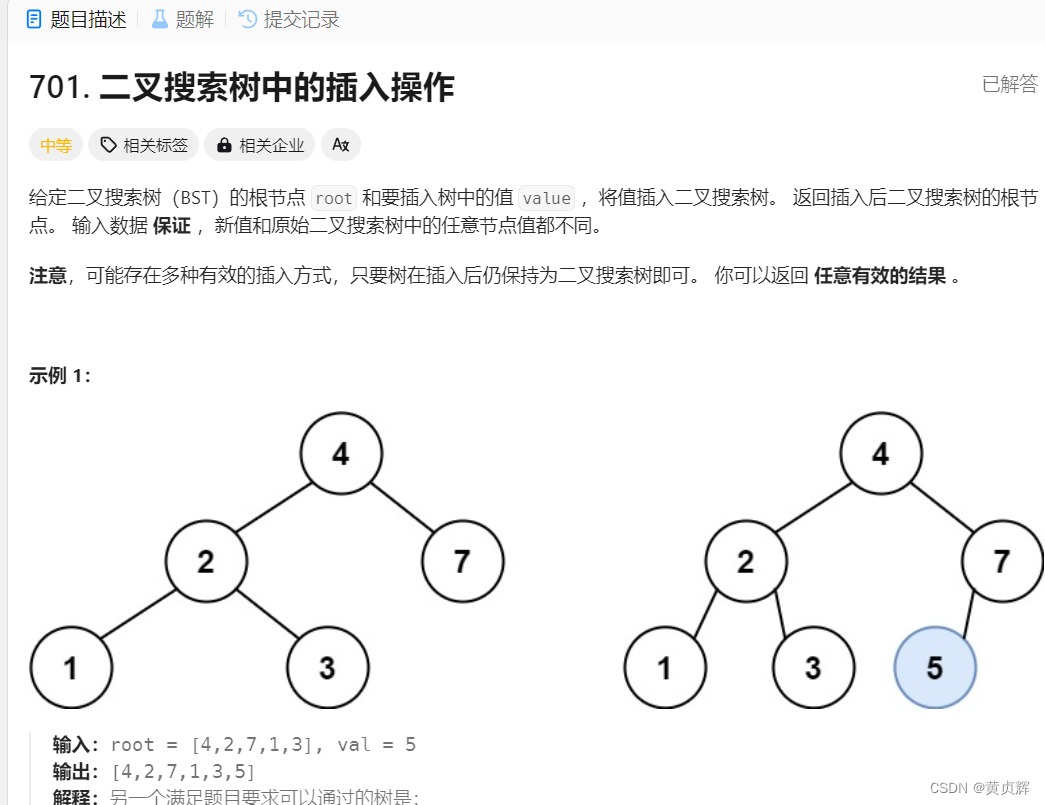
思路：往二叉搜索树中插入一个值，树的结构有多种符合的情况，那我们可以选一种最容易的插入方式，反正只需要插入一个值而已，我们不难发现，不管插入什么值，都可以安排插入到叶子节点上。
再利用二叉搜索树特性：val值比当前节点值大时，就往右遍历去放，反之相反，当遍历到空时，我们就新建一个节点，并且赋值给递归中的上一层节点。

class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        //当递归到节点为空时，新建这个新节点
            if (root == null) return new TreeNode(val);
            //二叉搜索树，val比当前节点值大，就往右遍历
            if(val < root.val ) {
                //把新建的节点，赋值过来
                root.left = insertIntoBST(root.left, val);  
            }else {
               root.right = insertIntoBST(root.right, val);  
            }
            return root;
            
    }
}