1 认识时间复杂度
1.1 什么是时间复杂度?
时间复杂度是一个函数,它定性描述该算法的运行时间,在软件开发中,时间复杂度就是用来方便开发者估算出程序运行时间,通常用算法的操作单元数量来代表程序消耗的时间,这里默认CPU的每个单元运行消耗的时间都是相同的。假设算法的问题规模为n,那么操作单元数量便用函数f(n)来表示,随着数据规模n的增大,算法执行时间的增长率和f(n)的增长率呈现一定的关系,这称作为算法的渐近时间复杂度,简称时间复杂度,记为 O(f(n)),其中n指的是指令集的数目。
1.2 什么是big O
big O用来表示算法执行时间的上界,也可以理解为最差情况下运行的时间,数据量和顺序等情况对算法的执行时间有非常大的影响,这里假设的是某个输入数据用该算法运行的时间,比其他数据的运算时间都要长。
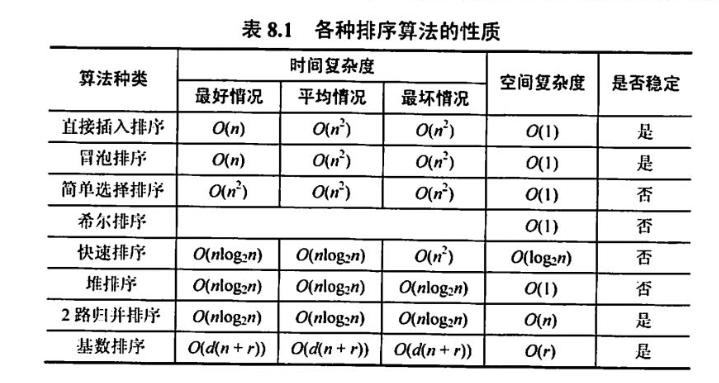
插入排序的时间复杂度我们都说是O(n^2) ,但是插入排序的时间复杂度和输入数据有很大的关系,假如输入数据是完全有序的,则插入排序的时间复杂度是O(n),假如输入的数据是完全倒序的,则时间复杂度是O(n^2),所以最坏是O(n^2) 的时间复杂度,我们说插入排序的时间复杂度为O(n^2)。
快速排序是O(nlogn),快速排序的在最差的情况下时间复杂度是O(n^2) ,一般情况下是O(nlogn),所以严格从big O的定义来讲,快速排序的时间复杂度应该是O(n^2),但是我们依然说快速排序的时间复杂度是O(nlogn),这是业内默认的规定。
二分查找的时间复杂度是O(logn),每次二分数据规模减半,直到数据规模减少为 1,最后相当于求2的多少次方等于n,相当于分割了logn次。
归并排序的时间复杂度是O(nlogn),自顶而下的归并,从数据规模为n分割到1,时间复杂度是O(logn),然后不断向上归并的时间复杂度是O(n),总体时间复杂度是O(nlogn)。
树的遍历复杂度一般是O(n),n是树的节点个数,选择排序时间复杂度是O(n^2),我们会在对应的章节逐步分析各个数据结构和算法的复杂度。更多的时间复杂度分析和推导可参阅主定理。
1.3 常见时间复杂度
1.3.1 O(1):常数复杂度
let n = 100;
1.3.2 O(logn):对数复杂度
//二分查找非递归
var search = function (nums, target) {
let left = 0,
right = nums.length - 1;
while (left <= right) {
let mid = Math.floor((left + right) / 2);
if (nums[mid] === target) {
return mid;
} else if (target < nums[mid]) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return -1;
};
1.3.3 O(n):线性时间复杂度
for (let i = 1; i <= n; i++) {
console.log(i);
}
1.3.4 O(n^2):平方 (嵌套循环)
for (let i = 1; i <= n; i++) {
for (let j = 1; j <= n; j++) {
console.log(i);
}
}
for (let i = 1; i <= n; i++) {
for (let j = 1; j <= 30; j++) { //嵌套的第二层如果和n无关则不是O(n^2)
console.log(i);
}
}
1.3.5 O(2^n):指数复杂度
for (let i = 1; i <= Math.pow(2, n); i++) {
console.log(i);
}
1.3.6 O(n!):阶乘
for (let i = 1; i <= factorial(n); i++) {
console.log(i);
}
2 常见排序算法
2.1 选择排序
算法步骤:
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
重复第二步,直到所有元素均排序完毕。
选择排序是一种简单直观的排序算法,无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间。
function selectSort(arr) {
for (let i=0;i<arr.length-1;i++) {
let min = i;
for (let j=min+1;j<arr.length;j++) {
if (arr[min] > arr[j]) {
min = j;
}
}
let temp = arr[i];
arr[i] = arr[min]
arr[min] = temp;
}
return arr;
}
2.2 冒泡排序
比较相邻的元素。如果第一个比第二个大,就交换它们两个;
第一遍循环0-n 确定n的值 都是找出最大的值冒泡在最上面
第二遍循环0-n-1 确定n-1的值
第三遍循环0-n-2 确定n-2的值
function bubleSort(arr) {
for (let i = 0;i<arr.length-1;i++) { // 循环轮次
for (let j=0;j< arr.length-i-1;j++) { // 每轮比较次数
if (arr[j] > arr[j+1]) { // 相邻比较
let temp = arr[j]
arr[j] = arr[j+1]
arr[j+1] = temp
}
}
}
return arr;
}
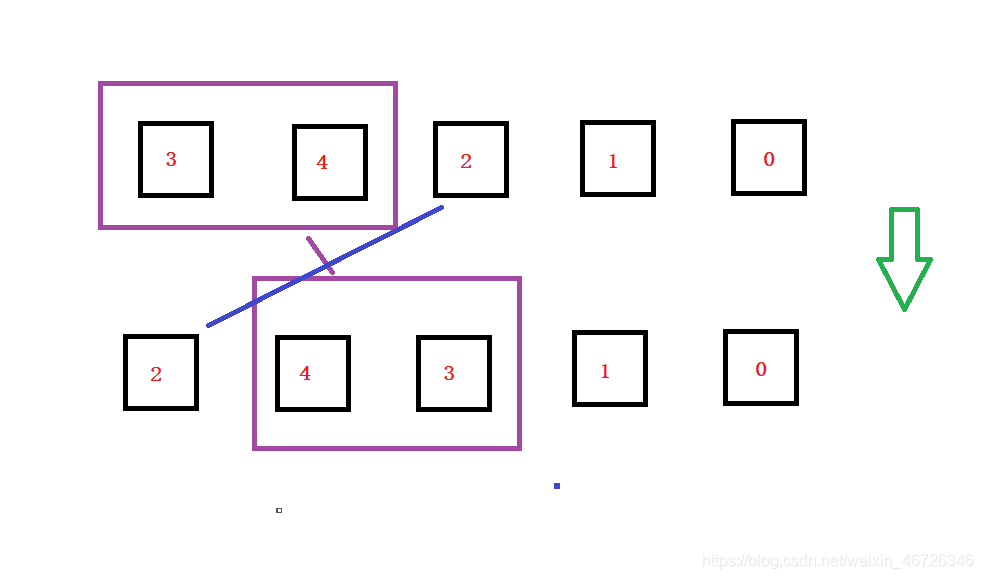
2.3 插入排序
第一次 前俩个数值排序
第二次循环 前三个数值排序,比较最后一个数值和新的数值,然后插入到指定位置
function insertSort(arr) {
for (let i = 1;i<arr.length;i++) { // 循环轮次
let end = i;
let curr = arr[i]
while(end > 0 && curr < arr[end-1]) { // 直到第一位 或者 当前的数不是最小值
arr[end] = arr[end - 1] // 移动比当前值小的值到后一位
end--
}
arr[end] = curr // 插入当前值
}
return arr;
}
2.4 异或运算
当且仅当只有一个表达式的某位上为 1 时,结果的该位才为 1。否则结果的该位为 0,简单的说就是-----相同为 0,不同为 1
语法:result = expression1 ^ expression2
按位异或 是对两个表达式执行 按位异或,先将两个数据转化为二进制数,然后进行 按位异或运算,只要位不同结果为 1,否则结果为 0
例如:
let a = 5;
let b = 8;
let c = a ^ b;
console.log(c) // 13
解析:
a 转二进制数为:0101
b 转二进制数为:1000
那么按照 按位异或 运算之后得到:1101(相同为 0,不同为 1),得到 c 的值就是 13
特点
一、满足交换率
a ^ b == b ^ a
二、两个相同的数字异或操作得到的一定是 0
a^a === 0
三、0 和 其他数字异或操作得到的一定是其他数字
0^a === a
2.5 练习题
一、给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素
let arr = [1, 3, 1, 2, 2, 7, 3, 6, 7]
// es5 解决方案
function fnc(arr){
let result = 0;
for(let i = 0; i < arr.length; i++){
result = result ^ arr[i];
}
return result;
}
// es6 解决方案
function fnc(arr){
return arr.reduce((a, b) => a ^ b, 0);
}