向量相似性度量的常用方法
- 0. 引言
- 1. 欧氏距离(Euclidean distance)
- 2. 余弦相似度(Cosine similarity)
- 3. 汉明距离(Hamming distance)
- 4. 点积相似度 (Dot Product Similarity)
- 5. 曼哈顿距离 (Manhattan Distance)
0. 引言
今天花时间学习学习向量相似性度量的常用方法,痛苦自己一次,以后就轻松了。😼
1. 欧氏距离(Euclidean distance)
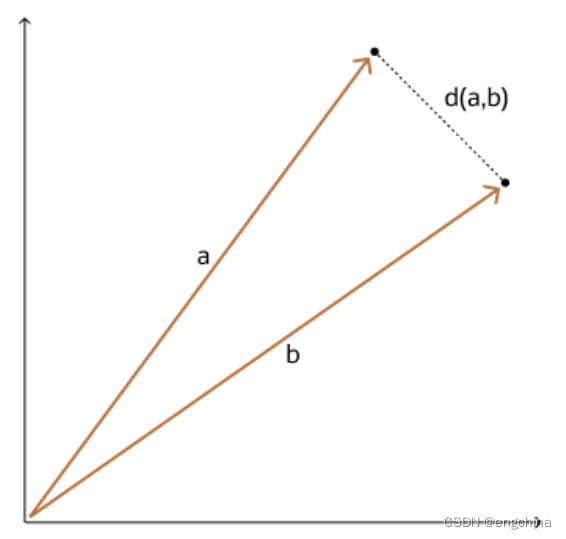
1.1 概念
欧氏距离是衡量两个向量之间“距离”的常用方法。它是在欧几里得空间中,两个点之间的最短直线距离。
1.2 计算公式
对于 n 维向量 x 和 y,欧氏距离计算公式如下:
d(x, y) = sqrt((x1-y1)^2 + (x2-y2)^2 + ... + (xn-yn)^2)
其中,x1, x2, …, xn 是 x 向量中的元素,y1, y2, …, yn 是 y 向量中的元素。
1.3 应用场景
欧氏距离在许多领域都有应用,例如:
- 机器学习:欧氏距离常用于 k 最近邻算法 (KNN) 中,计算样本之间的距离
- 图像检索:欧氏距离常用于图像检索中,计算图像之间的相似度
- 推荐系统:欧氏距离常用于推荐系统中,计算用户之间的相似度
2. 余弦相似度(Cosine similarity)
2.1 概念
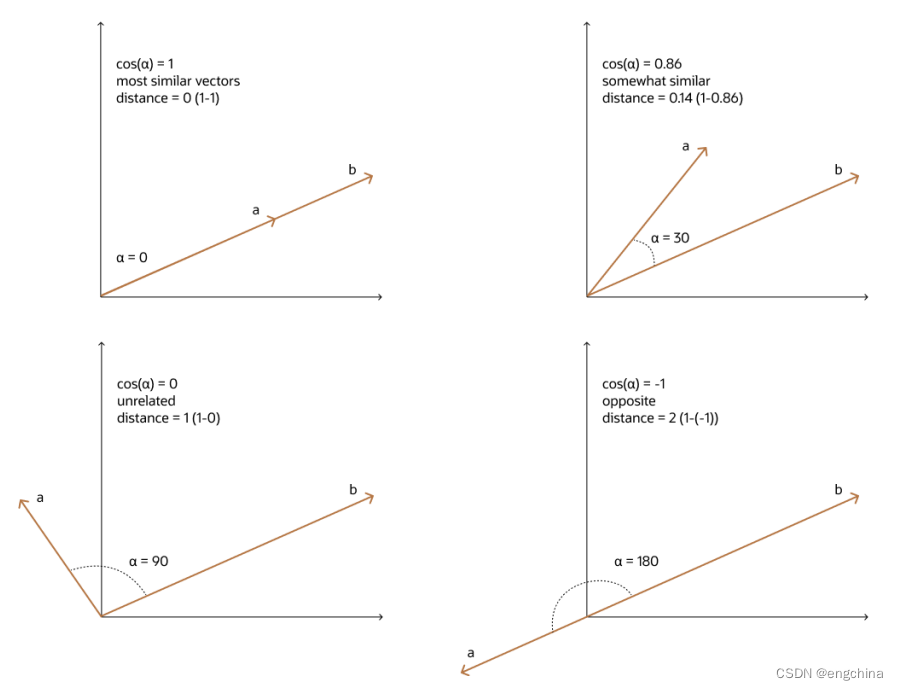
余弦相似度是衡量两个向量之间“方向”相似程度的常用方法。它是在向量空间中,两个向量夹角的余弦值。
2.2 计算公式
对于 n 维向量 x 和 y,余弦相似度计算公式如下:
cos(x, y) = (x1*y1 + x2*y2 + ... + xn*yn) / (||x|| * ||y||)
其中,x1, x2, …, xn 是 x 向量中的元素,y1, y2, …, yn 是 y 向量中的元素,||x|| 和 ||y|| 分别是 x 和 y 向量的模长。
向量的模长公式
对于 n 维向量 x,其模长计算公式如下:
||x|| = sqrt(x1^2 + x2^2 + ... + xn^2)其中,x1, x2, …, xn 是 x 向量中的元素。
2.3 应用场景
余弦相似度在许多领域都有应用,例如:
- 文本检索:余弦相似度常用于文本检索中,计算文本之间的相似度
- 自然语言处理:余弦相似度常用于自然语言处理中,计算词语之间的相似度
- 信息检索:余弦相似度常用于信息检索中,计算文档之间的相似度
3. 汉明距离(Hamming distance)
3.1 概念
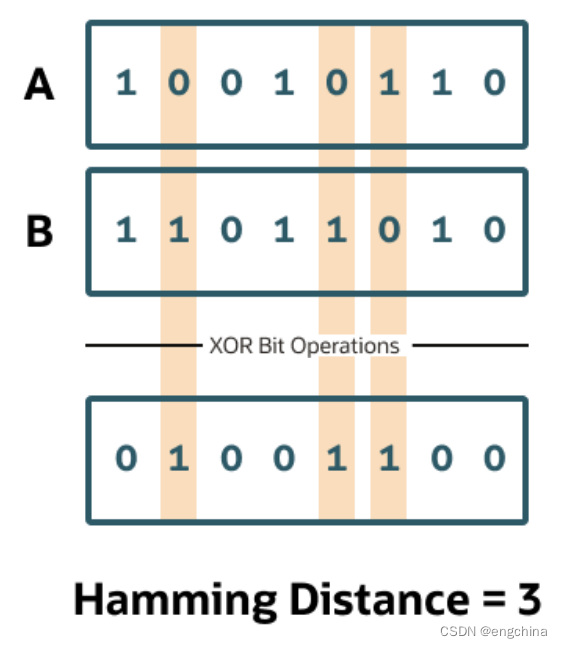
汉明距离是衡量两个相同长度的字符串之间“差异”的常用方法。它是两个字符串中不同字符的数量。
3.2 计算公式
对于两个长度为 n 的字符串 x 和 y,汉明距离计算公式如下:
d(x, y) = n - Σ(x[i] == y[i])
其中,x[i] 和 y[i] 分别是 x 和 y 字符串中第 i 个字符,Σ 表示求和运算。
3.3 应用场景
汉明距离在许多领域都有应用,例如:
- 通信:汉明距离常用于通信中,检测数据传输中的错误
- 信息论:汉明距离常用于信息论中,衡量两个信息源之间的差异
- 生物学:汉明距离常用于生物学中,比较 DNA 序列
4. 点积相似度 (Dot Product Similarity)
4.1 点积相似度定义
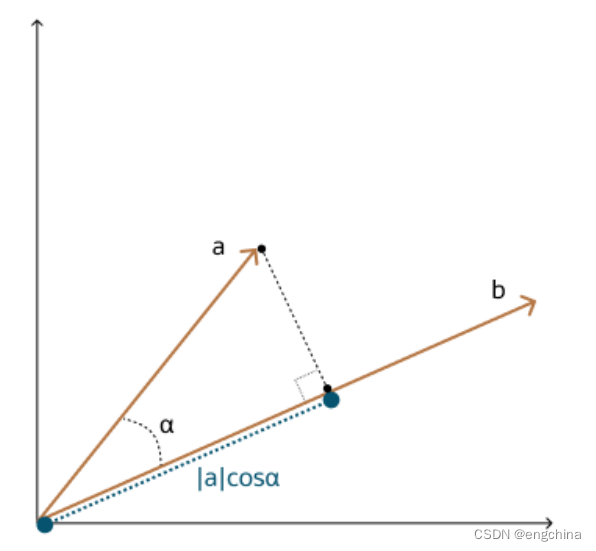
点积相似度 (Dot Product Similarity) 是衡量两个向量之间“相似度”的常用方法。它是两个向量的点积除以它们的模长的乘积。
4.2 点积相似度计算公式
对于 n 维向量 x 和 y,点积相似度计算公式如下:
sim(x, y) = (x * y) / (||x|| * ||y||)
其中,x * y 表示 x 和 y 的点积,||x|| 和 ||y|| 分别表示 x 和 y 向量的模长。
4.3 点积相似度性质
点积相似度具有以下性质:
- **范围:**点积相似度的范围是 [-1, 1]。
- **相似性:**点积相似度越大,两个向量越相似。
- **正交性:**如果两个向量正交,则它们的点积相似度为 0。
4.4 点积相似度应用场景
点积相似度在许多领域都有应用,例如:
- **文本检索:**点积相似度常用于文本检索中,计算文本之间的相似度
- **自然语言处理:**点积相似度常用于自然语言处理中,计算词语之间的相似度
- **推荐系统:**点积相似度常用于推荐系统中,计算用户之间的相似度
4.5 点积相似度与余弦相似度
点积相似度与余弦相似度密切相关。余弦相似度是点积相似度的一种归一化形式。它们之间的关系如下:
cos(x, y) = sim(x, y)
5. 曼哈顿距离 (Manhattan Distance)
5.1 曼哈顿距离定义
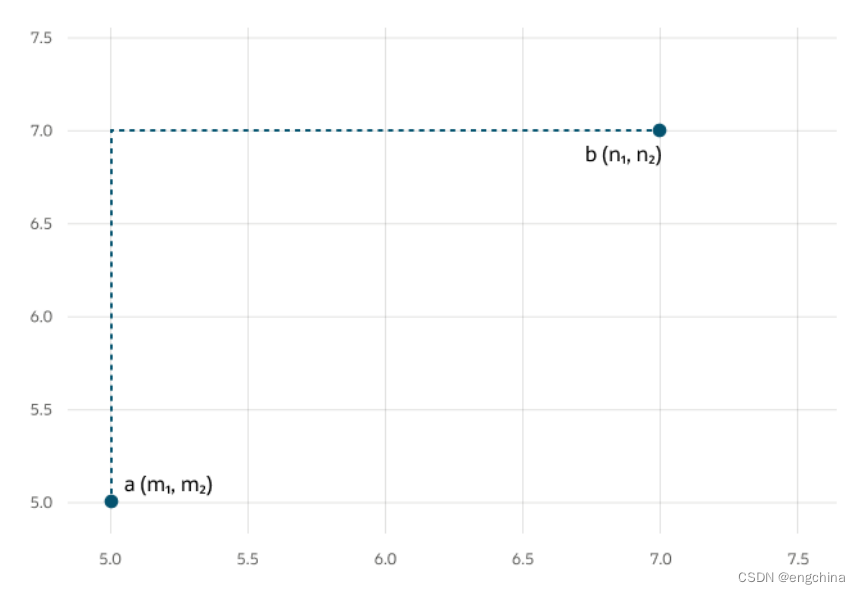
曼哈顿距离 (Manhattan Distance) 是衡量两个向量之间“距离”的常用方法。它是两个向量对应分量差的绝对值的总和。
5.2 曼哈顿距离计算公式
对于 n 维向量 x 和 y,曼哈顿距离计算公式如下:
d(x, y) = |x1-y1| + |x2-y2| + ... + |xn-yn|
其中,x1, x2, …, xn 是 x 向量中的元素,y1, y2, …, yn 是 y 向量中的元素。
5.3 曼哈顿距离性质
曼哈顿距离具有以下性质:
- **非负性:**曼哈顿距离是非负的,对于任意向量 x 和 y,都有 d(x, y) >= 0。
- 对称性:曼哈顿距离是对称的,对于任意向量 x 和 y,都有 d(x, y) = d(y, x)。
- **三角不等式:**曼哈顿距离满足三角不等式,对于任意向量 x、y 和 z,都有 d(x, z) <= d(x, y) + d(y, z)。
5.4 曼哈顿距离与欧几里得距离
曼哈顿距离与欧几里得距离是两种常用的距离度量方法。它们的区别在于:
- 曼哈顿距离是各个分量差的绝对值的总和,而欧几里得距离是各个分量差的平方和的平方根。
- 曼哈顿距离的计算速度更快,而欧几里得距离的计算精度更高。
5.5 曼哈顿距离应用场景
曼哈顿距离在许多领域都有应用,例如:
- **图像处理:**曼哈顿距离常用于图像处理中,计算图像之间的差异
- **机器学习:**曼哈顿距离常用于机器学习中,计算样本之间的距离
- **数据挖掘:**曼哈顿距离常用于数据挖掘中,计算数据点之间的相似度
完结!