---

 本章节是前缀和的延申

 

一命通关前缀和-CSDN博客https://blog.csdn.net/qq_74260823/article/details/136530291?spm=1001.2014.3001.5501

 一命通关前缀和

---

公交车

引入

还是利用我们在前缀和中所采用的例子——公交车。

有一辆公交车，一共上下了N批乘客：

1. 第一批2个人，第一站上车，第五站下车
2. 第二批6个人，第三站上车，第六站下车
3. 第三批4个人，第二站上车，第五站下车
4. ... 

问，在不查公交车监控的情况下，公交车到达每一站的时候车上还剩下几个人？

这个问题，传统的解决方法很直接，我们创建一个数组

，k为数组大小车站的数目

用来表示每一站的时候，车上还剩几个人。

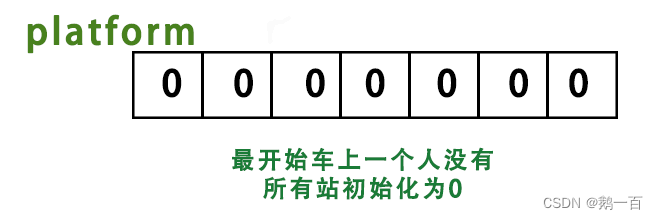
而对每一批上下车的乘客，假设他们有people个人在第up站上车，在第off站下车，他们在车上的站数为[up,off)，也就是说，数组i到j中的所有元素都要加上他们的人数people

 用以上方法，来表示前三批人：

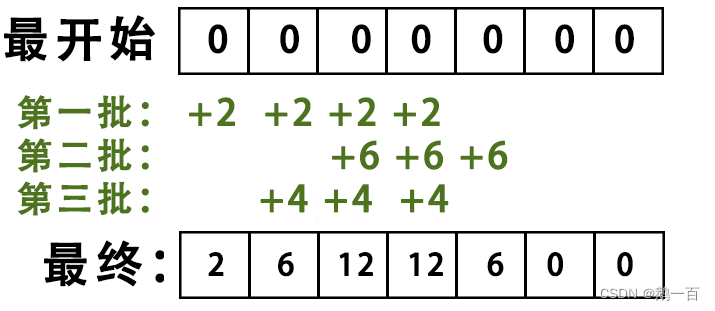
假设有N批人，公交车一共有k站，每一批人都是第一站上最后一站下，那最坏的时间复杂度是多少？O(Nk)。有没有办法把这个解法优化一下，让每一批人的计算都变成O(1)呢？当然有：

优化

我们想让每一批人的计算都变成O(1)，那就想办法，最大化利用第up站上和第off站下的信息。我们有没有办法，只需要表示第i站和第j站的人数变化，就能表示所有站的人数变化？

如果你有办法，就不会继续看这篇文章了。直接说结论吧：当然有。我们来重新挖掘一下这个信息：

• 第up站上people人，表示公交车上从第up站开始，往后都多了people个人
• 第off站下people人，表示公交车上从第off站开始，往后都少了people个人
• 而在off站之后，多people个人和少people个人加在一起，最终是0个人，也就是第up站上第off站下，只对[up,off)这些站台会产生影响，对其他站台产生不了任何影响，从而得到了我们的传统解法。

我们利用这个信息，再创立一个数组：

用来表示每一站和前一站的人数差，

而再来通过这个数组去整理题目的信息：

• 第二站上了四个人，也就是从第二站开始，比第二站之前都要多出四个人，自然第二站比第一站要多四个人，
• 第三站和第二站，都比第一站多四个人，第二站和第三站的差没有变化，故dif[3]不变
• 第五站下了四个人，也就是从第五站开始，比第五站之前都要少四个人，自然第五站比第四战要少四个人， 
• 同理，第六站和第五站的差也没有发生变化，故dif[6]不变 

通过这个，我们自然可以总结出规律：

这样，每一批的上下车，时间复杂度都优化为了O(1)

但是，有人可能就要问了，海老师海老师，这个数组有什么用啊？这又不是最终的答案
别急，往后有反转

求解 

假设，公交车有一个第0站，第0站的人数肯定是0人

• 我们知道了第1站和第0站的人数差，第一站的人数很容易求出来 
• 而接着往后，第二站和第一站的人数差我们也知道，自然 
• 很容易便找到规律：对于每一站i，都可以求得
   

而把所有的platform展开，就能得到：
 

也就是，platform的值为dif数组i之前所有元素的和

好了，跳出公交车。我们通过这个解答，发现platform就是前缀和数组，而对前缀和数组的每一项求差得到的dif数组，我们称之为差分数组。我们发现了
而

也就是，dif[i]和nums[i]其实是一回事，这就是我们常说的

好了，知道这句话其实卵用没有，我们直接来看代码吧。

代码及公式

//假设一个数组 vector<int> people中有三个元素[up,off,people]
//现在给了一个二元数组 vector<vector<int>> nums，大小为n，表示有N批乘客
//求解每一站的乘客人数

//自然，初始化两个数组，platform和dif
vector<int> platform(n+1);//因为假定了一个第0站，所以多开一块空间
vector<int> dif(n+1);//差分数组

for(auto& e:nums)
{
    int up=e[0];
    int off=e[1];
    int people=e[2];
    
    dif[up]+=people;
    dif[off]-=people;
    //每一次都是O(1),一共有n次，时间复杂度为O(n)
}

//再来求前缀和
for(int i=1;i<k+1;i++)
    platform[i]=platform[i-1]+dif[i];
//时间复杂度为站台数量O(k)
//总的时间复杂度为O(n+k)

这类题目的特征在于，每一次操作都对一块区间内的所有元素进行同样的操作。
面对这样的问题，我们先用差分数组，来把这些同样的操作，只表示出其区间首尾的变化
然后对差分数组求出前缀和，就能表示出总的变化

这便是差分数组的公式。

好了，有了这个公式，去乱杀差分的题目吧：

1109. 航班预订统计 - 力扣（LeetCode）

2251. 花期内花的数目 - 力扣（LeetCode）

---