目录
前言
一:树
1.树的概念
2.树的基础概念知识
3.在树中孩子节点和父节点知一求一
4.树的表示方法
二:二叉树
1.二叉树的概念
2.二叉树的特性
3.满二叉树
4.完全二叉树
三:堆
1.堆的定义
2.堆的实现:数组实现
1.堆的结构定义
2.堆的实现
3.堆排序
第一种:直接排序
第二种:建堆实现
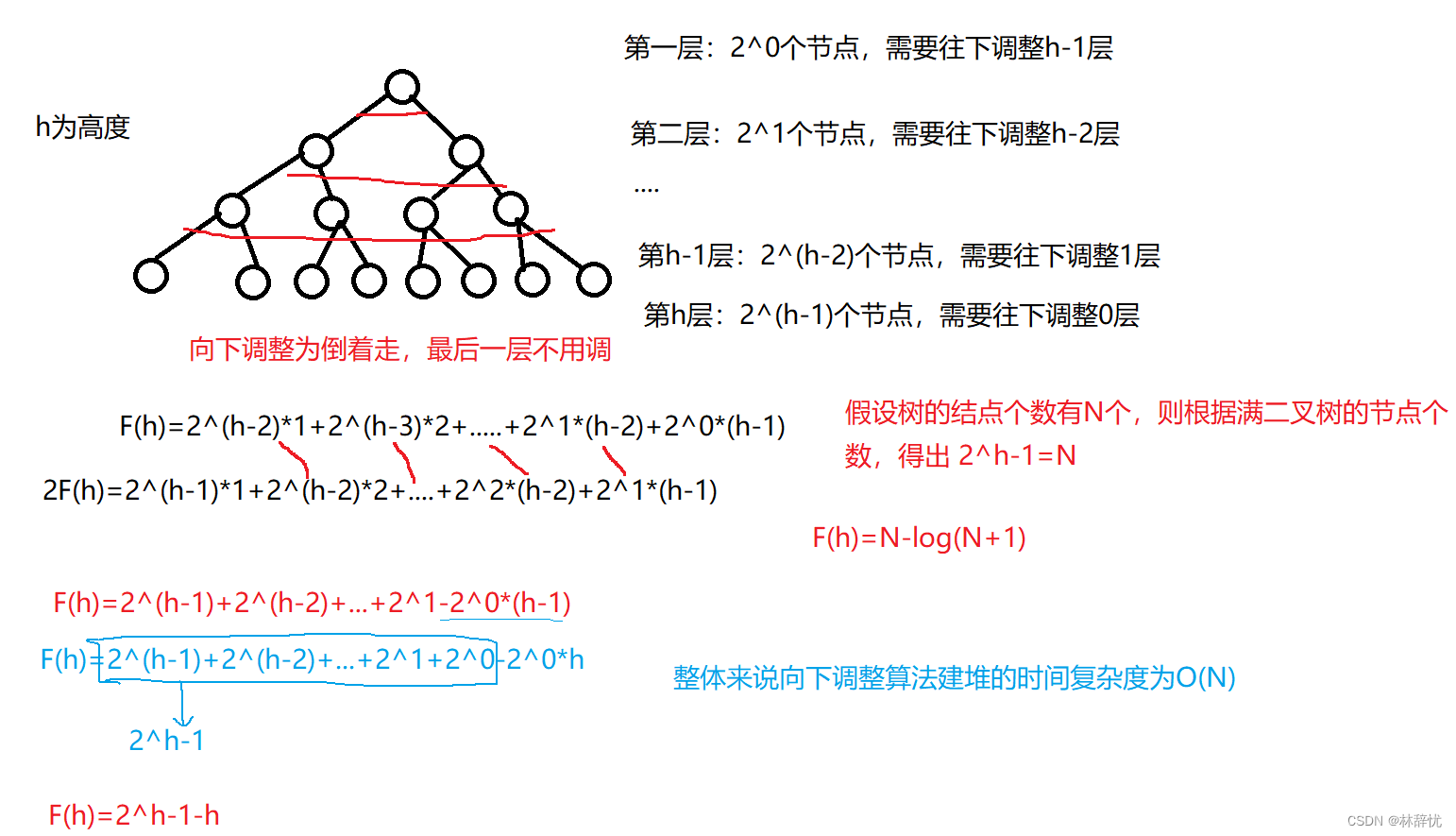
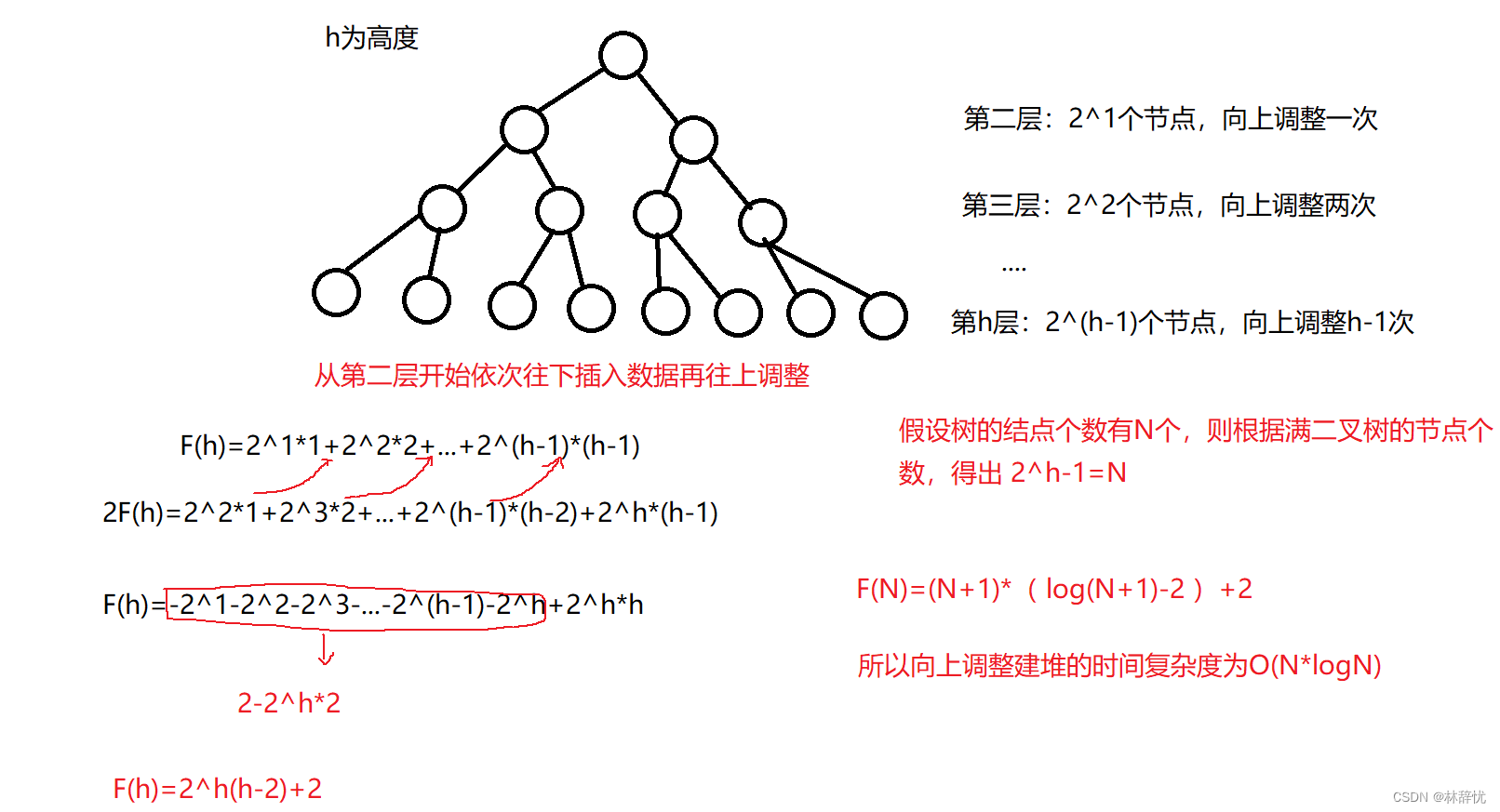
4.堆排序中向下调整建堆和向上调整建堆时间复杂度比较
1.向下调整建堆
2.向上调整建堆
5.堆实现TopK 问题
TopK问题就是从N个数中找出最大或最小的前K个
1.正常思路
2.改进思路
3.TopK问题的实现(用文件进行操作)
四:结束语

接下来的日子会顺顺利利,万事胜意,生活明朗-----------林辞忧
前言
数据结构的树是一种较复杂的结构,包含多种分支结构,如完全二叉树,满二叉树,堆,以及更难理解的AVL树,B数,B+树等等,这些结构共同组成了树的庞大结构体系,接下来我们将初步了解关于树,堆等结构
一:树
1.树的概念
树是一种非线性的数据结构,是由N个节点连接而成,当N为0时称为空树
2.树的基础概念知识

3.在树中孩子节点和父节点知一求一
知孩子节点算父亲节点:parent=(child-1)/2;
知父节点求孩子节点:child=parent*2+1(假设只有一个孩子)
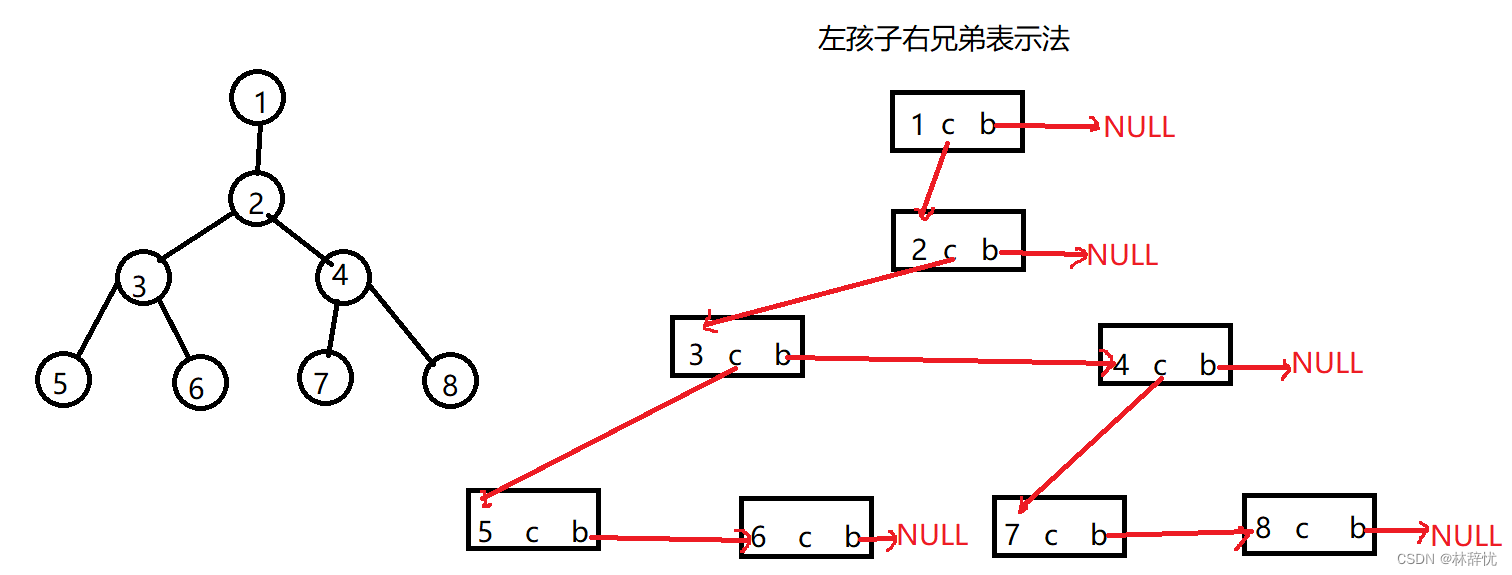
4.树的表示方法
左孩子右兄弟表示法
二:二叉树
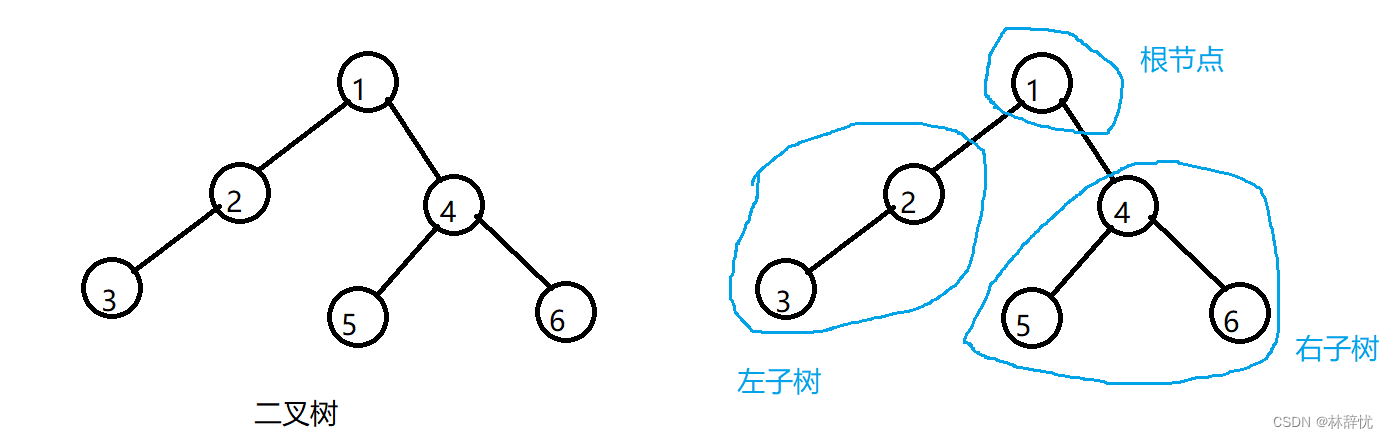
1.二叉树的概念
是n个节点连接而成的有限集合,分为根节点和根节点的左右子树,且两棵子树不相交
2.二叉树的特性
1.每个节点最多两棵子树,即不存在度为2以上的节点
2.二叉树的左右子树是有顺序,不能颠倒的,为有序树
3.满二叉树
每一层都是满结点的二叉树
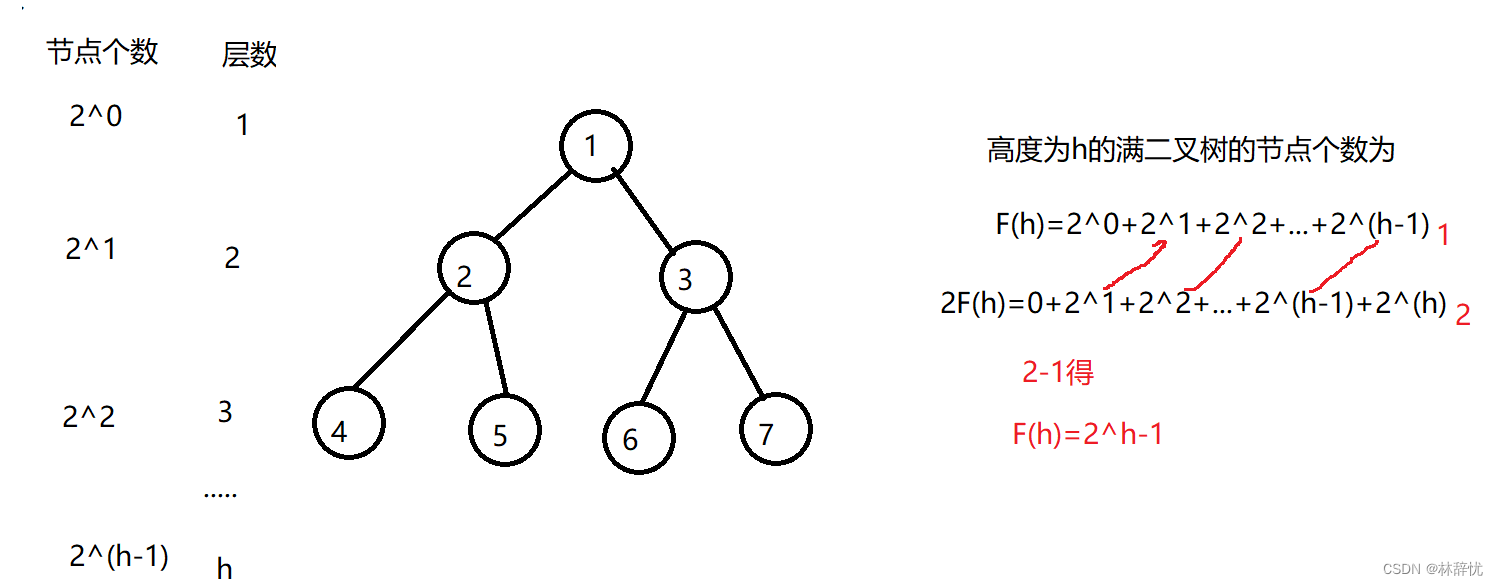
4.完全二叉树
前h-1层都是满的,最后一层可以不满,但是从左往右是连续的
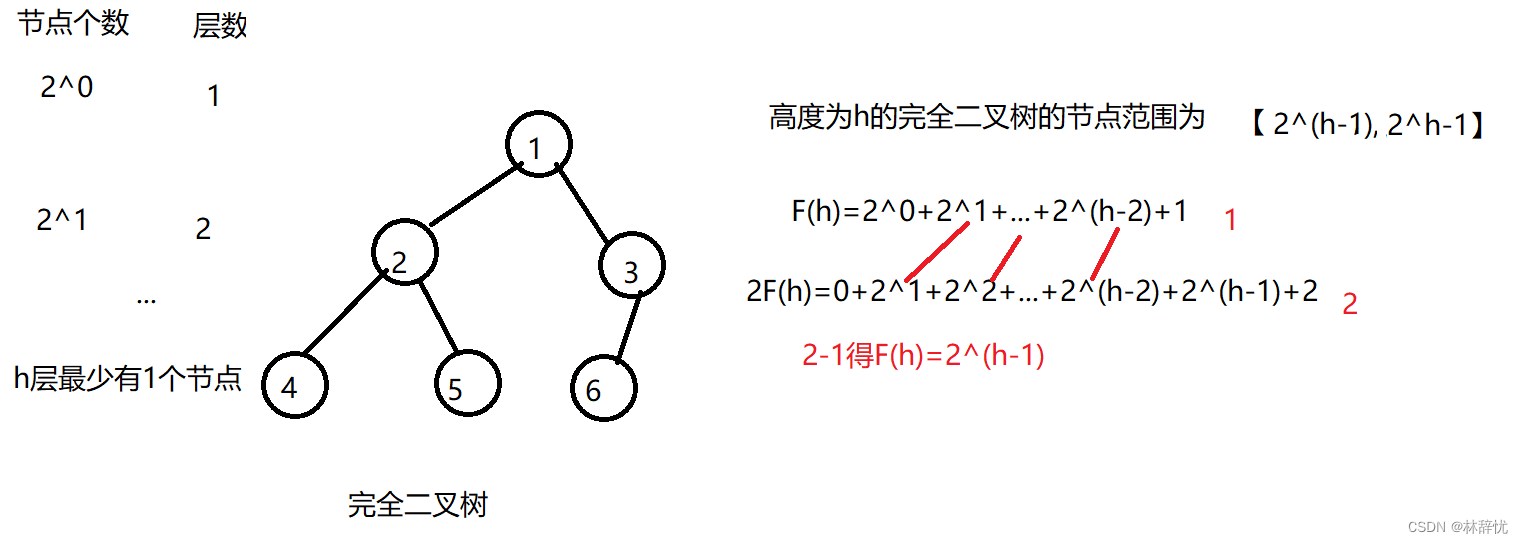
三:堆
1.堆的定义
1.堆属于完全二叉树的一种,分为大根堆和小根堆
2.大根堆:树的任何一个父节点都大于或等于孩子节点
3.小根堆:树的任何一个父节点都小于或等于孩子节点
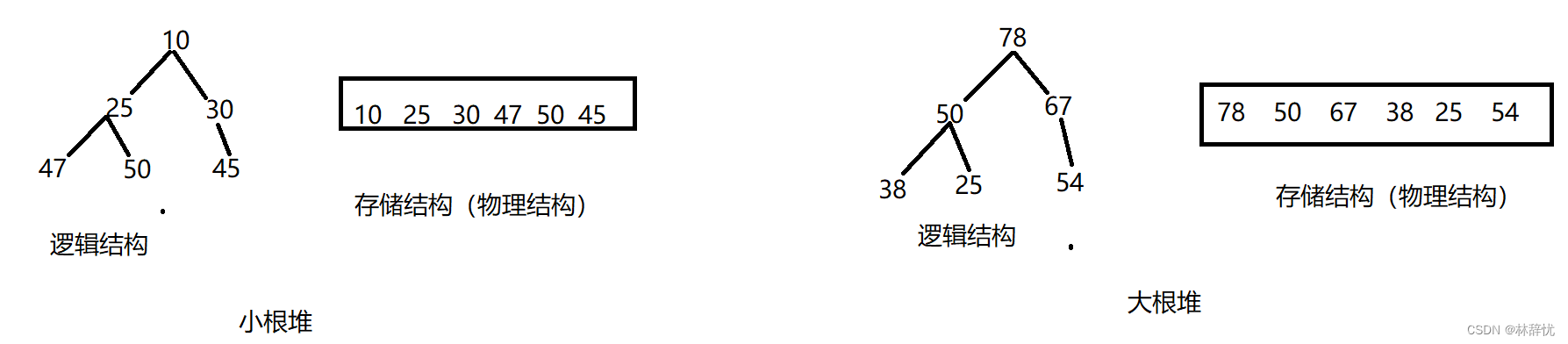
2.堆的实现:数组实现
1.堆的结构定义

2.堆的实现

#include "Heap.h"
//堆的初始化
void HeapInit(Heap* php)
{
assert(php);
php->a = NULL;
php->capacity = php->size = 0;//指向最后一个有效数据的下一个
}
//堆的销毁
void HeapDestroy(Heap* php)
{
assert(php);
free(php->a);
php->a = NULL;
php->capacity = php->size = 0;
}
//堆中插入数据
void HeapPush(Heap* php, HeapDataType x)
{
assert(php);
if (php->capacity == php->size)
{
int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
HeapDataType* tmp = realloc(php->a, sizeof(HeapDataType) * newcapacity);
if (tmp == NULL)
{
perror("malloc fail\n");
return;
}
php->a = tmp;
php->capacity = newcapacity;
}
php->a[php->size++] = x;
//向上调整保持堆结构
AdjustUp(php->a, php->size-1);
}
void Swap(HeapDataType* p1, HeapDataType* p2)
{
HeapDataType tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void AdjustUp(HeapDataType* a, int child)
{
int parent = (child - 1) / 2;
while (child>0)
{
//小堆
if (a[parent] > a[child])
{
//交换
Swap(&a[parent], &a[child]);
//迭代往上
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
//删除堆顶元素
void HeapPop(Heap* php)
{
assert(php);
assert(!HeapEmpty(php));
Swap(&php->a[0], &php->a[php->size - 1]);
php->size--;
//向下调整
AdjustDown(php->a, php->size, 0);
}
void AdjustDown(int* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
if (child + 1 < n && a[child] > a[child + 1])
{
child++;
}
if (a[parent] > a[child])
{
Swap(&a[parent], &a[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//判空
bool HeapEmpty(Heap* php)
{
return php->size == 0;
}
//堆顶元素
HeapDataType HeapTop(Heap* php)
{
return php->a[0];
}
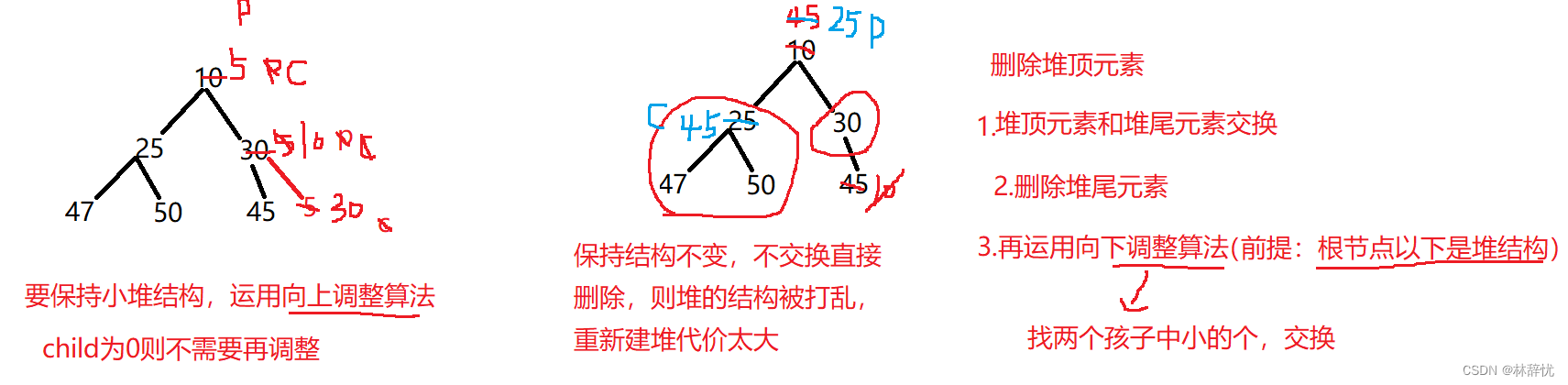
3.堆排序
堆排序作为一种排序方法,时间复杂度为O(N*log N),排序效率极佳,接下来我们将详细介绍
第一种:直接排序
void HeapSort(int* a, int n)
{
Heap hp;
HeapInit(&hp);
int b[] = { 25,10,45,47,30,50 };
int sz = sizeof(b) / sizeof(b[0]);
for (int i = 0; i < sz; i++)
{
//插入数据调整为堆
HeapPush(&hp, b[i]);
}
int i = 0;
while (!HeapEmpty(&hp))
{
//再插入回数组
int top = HeapTop(&hp);
a[i++] = top;
HeapPop(&hp);
}
printf("\n");
}弊端:需要先写一个堆,太复杂
第二种:建堆实现

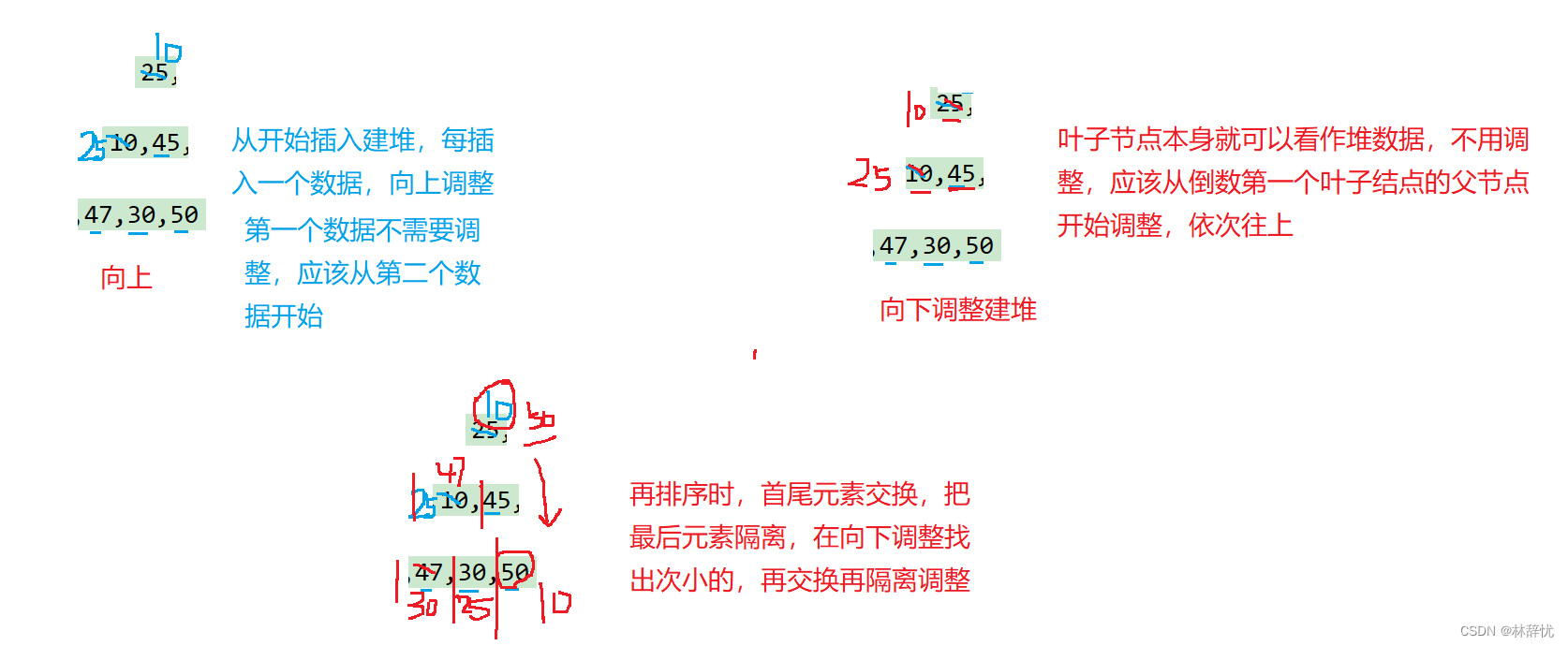
4.堆排序中向下调整建堆和向上调整建堆时间复杂度比较
1.向下调整建堆
2.向上调整建堆
5.堆实现TopK 问题
TopK问题就是从N个数中找出最大或最小的前K个
1.正常思路
如果找N个数中最大的前K个,就得把N个数建为大堆,每Pop一次找到次大的数(Pop函数在每次Pop时会往下调整找出次大的数),Pop K次,即可找到前K个
如果当数据很大时,上面的思路就处理不了,比如N为10亿个整数,就得用4G的存储空间,此时数据就会存储在磁盘文件中,不允许随机访问等操作
2.改进思路
1.建立K个数的小堆
2.后N-K个数,依次与堆顶数据比较,大的话就替换入堆(覆盖堆顶值,向下调整)
3.最后这个小堆的值就是最大的前K个
3.TopK问题的实现(用文件进行操作)
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
void AdjustDown(int* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
if (a[child + 1] < a[child])
{
child++;
}
if (a[parent] > a[child])
{
int tmp = a[parent];
a[parent] = a[child];
a[child] = tmp;
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void CreateNData()
{
//造数据
int n = 1000;
srand( (unsigned int) time(0) );
const char* file = "data.txt";
FILE* fin = fopen(file, 'w');
if (fin == NULL)
{
perror("fopen error\n");
return;
}
for (size_t i = 0; i < n; i++)
{
int x = rand() % 1000000;
fprintf(fin,"%d",x);
}
fclose(fin);
}
void PrintTopK(int k)
{
const char* file = "data.txt";
FILE* fout = fopen(file, 'r');
if (fout == NULL)
{
perror("fopen error\n");
return;
}
//建立k个数的小堆
int* kminheap = (int*)malloc(sizeof(int) * k);
if (kminheap == NULL)
{
perror("malloc fail\n");
return;
}
for (int i = 0; i < k; i++)
{
fscanf(fout, "%d", &kminheap[i]);
}
//建小堆
for (int i = (k - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(kminheap, k, i);
}
//堆顶元素和N-K个数据比较,大的话替换入堆
int val = 0;
while (!feof(fout))
{
fscanf(fout, "%d", &val);
if (val > kminheap[0])
{
kminheap[0] = val;
AdjustDown(kminheap, k, 0);
}
}
//打印数据
for (int i = 0; i < k; i++)
{
printf("%d ",kminheap[i]);
}
printf("\n");
}
int main()
{
CreateNData();
PrintTopK(5);
return 0;
}四:结束语
在初步了解这些二叉树和堆的结构和实现后,可以更方便为以后学习打下基础
低头往前冲吧