1.树

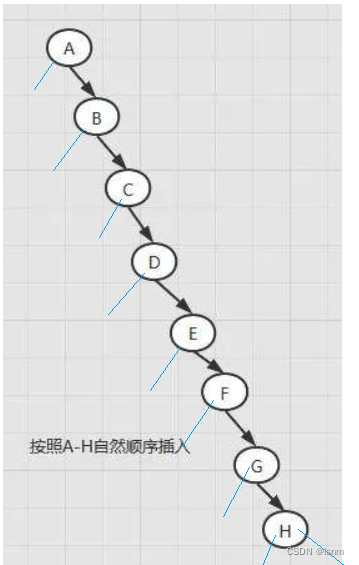
任何一棵树,都应该被观察成根和子树。
什么是根和子树呢?
我们利用人与人之间的关系来形象化了解 树 这种数据结构:
节点的度 :一个节点含有的子树的个数称为该节点的度;叶节点或终端节点 :度为 0 的节点称为叶节点;非终端节点或分支节点 :度不为 0 的节点;双亲节点或父节点 :若一个节点含有子节点,则这个节点称为其子节点的父节点;孩子节点或子节点 :一个节点含有的子树的根节点称为该节点的子节点;兄弟节点 :具有相同父节点的节点互称为兄弟节点;树的度 :一棵树中, 最大的节点的度称为树的度 ;节点的层次 :从根开始定义起,根为第 1 层,根的子节点为第 2 层,以此类推;树的高度或深度 :树中节点的最大层次;堂兄弟节点 :双亲在同一层的节点互为堂兄弟;节点的祖先 :从根到该节点所经分支上的所有节点;子孙 :以某节点为根的子树中任一节点都称为该节点的子孙。森林 :由 m ( m>0 )棵 互不相交 的树的集合称为森林
“子树都是递归定义的”,所以所有的子树都可以以相同的方法拆解、观察:
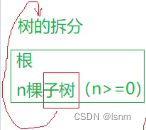
子树之间应当绝对独立,否则有环的话就是另一种数据结构——图
2.尝试与选型
没有规定一棵树有多少个孩子
因此,一棵树中的任意节点到底需要存多少个指针对于我们来说是未知的。
如果使用定长数组,势必会造成浪费(有的节点的度很大,有的很小)

也可以采用每个树节点中都放顺序表的方法,顺序表作为指针数组存放每一个子树地址(因为是指针数组的指针,所以subA应该为结构体二级指针)。
下面来了解最常用的树的表示法。
2.1左孩子右兄弟表示法
struct TreeNode{
int val;
struct TreeNode* leftchild;
struct TreeNode* nextbrother;
}但是请注意,“亲兄弟”才算“兄弟”。
对于树
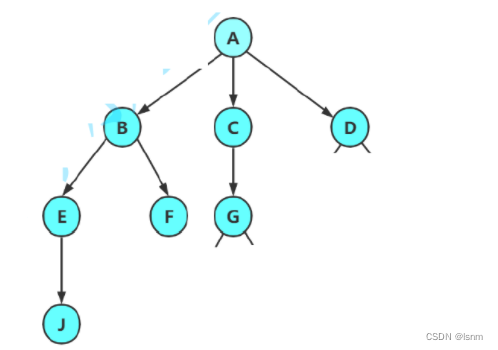
其中的指针指向就是
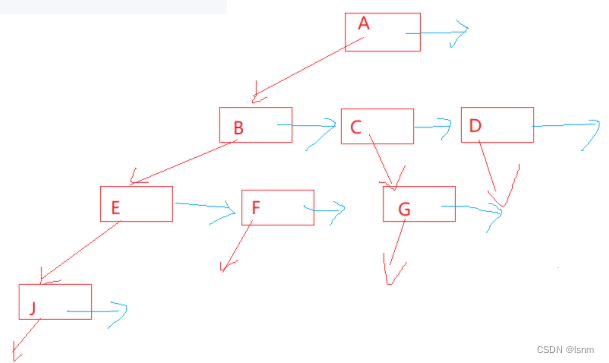
如果没有左儿子与右兄弟了,我们便让这个结构的相对应的指针指向空。
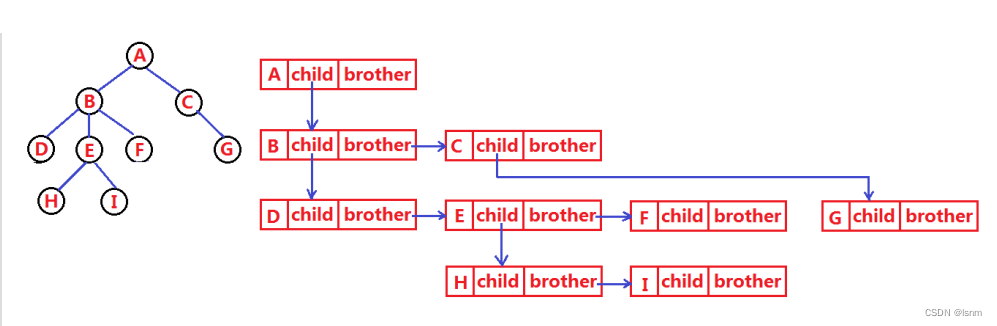
若一个父亲想找所有的儿子,就可以:
struct TreeNode* cur;
cur=A->leftchild;
while(cur){
//...................
cur=cur->next;
}
2.2双亲表示法:
也就是用下标和深度来实现。
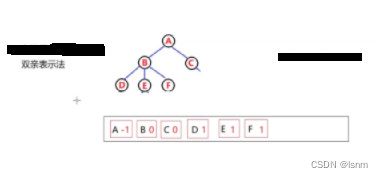
(之后的并查集也是这样使用 )
每一个节点存放数据和父亲所在的下标,类似于KMP匹配算法的感觉。A没有父亲,所以存放不存在的下标-1,B、C存放父亲(A)的下标0,以此类推
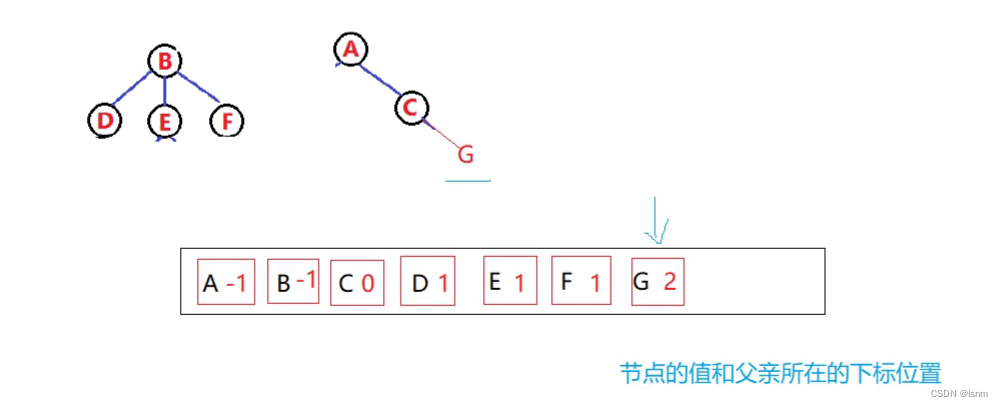
(尽管物理结构是数组,其实逻辑结构是森林)
3.二叉树
简单来说,每个节点最多两个孩子的树,就是二叉树(但不是一定有两个孩子,也可以作为叶子或者只有一个儿子),也叫BinaryTree、B树等。
3.1搜索二叉树
B树单纯的用来存储数据意义不大,并不如链表和顺序表。其结构存在意义之一如下图的“搜索二叉树”
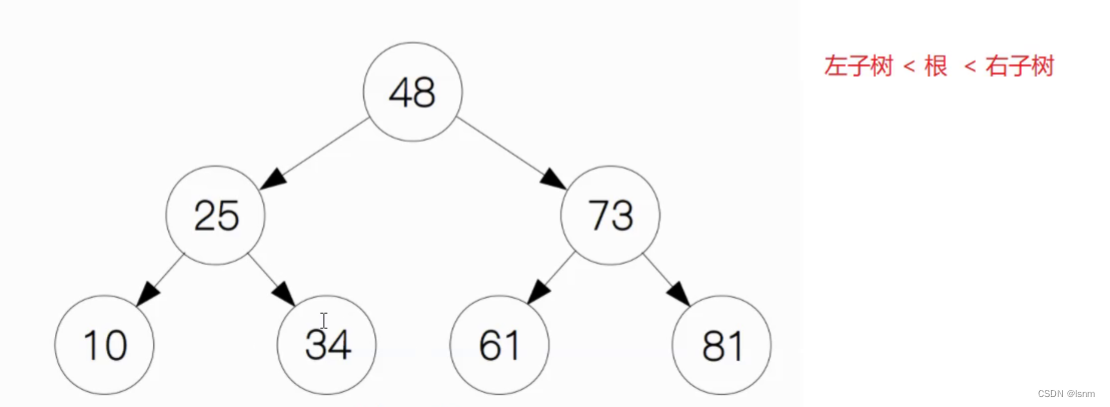
搜索二叉树同时具有存储数据和插入数据的功能
并且最多查找当前树高度次就能找到需要的数据:
因为搜索二叉树满足左子树<根<右子树(左子>树根>右子树同理),比方要搜索数据34,先与48比较,34小于48所以找左儿子25(后文中叫做leftchild或者左子树),34大于25所以找右儿子,成功匹配。每一次搜索都是向下走一层,所以最多搜索树的高度次就能到叶子的位置,效率极高。若要查找的是35,我们按照规则向下一直走到叶子的位置都未能找到,说明该树中不包含35,匹配失败
3.2完全二叉树
先来了解完全二叉树的特殊形式:满二叉树
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为 K ,且结点总数是,则它就是满二叉树。
也就是说,满二叉树必须所有非叶节点都有两个后代。
我们再了解一下二叉树的编号命名规则:根为0号,每一辈都从左到右(第一个leftchild 第一个rightchild 第二个leftchild 第二个rightchild)依次编号,编为一辈,再编下一辈。
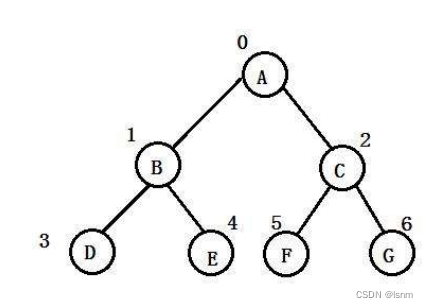
完全二叉树 :完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树引出来的。对于深度为 K 的,有n 个结点的二叉树,当且仅当其每一个结点都与深度为 K 的满二叉树中编号从 1 至 n 的节点一一对应时,称之为完全二叉树。 要注意的是 满二叉树是一种特殊的完全二叉树
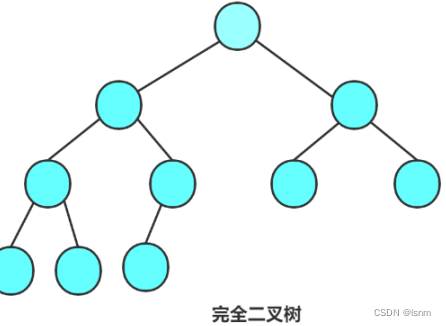
完全二叉树的部分规律
规律1:有两个儿子的节点个数+1=叶子结点
也就是对于首项为1,公比为2的等比数列中,前n-1项之和加一等于第n项。根据满二叉树可得,an就是叶子结点数,s(n-1)就是有两个儿子的节点数。
我们再以此推广到完全二叉树:每一个正常结点变成一个单儿子节点,就会损失相同个数的叶子节点和有两个儿子的节点(包括他自己),所以在“损失”的累积后,等式依然成立。

规律2:
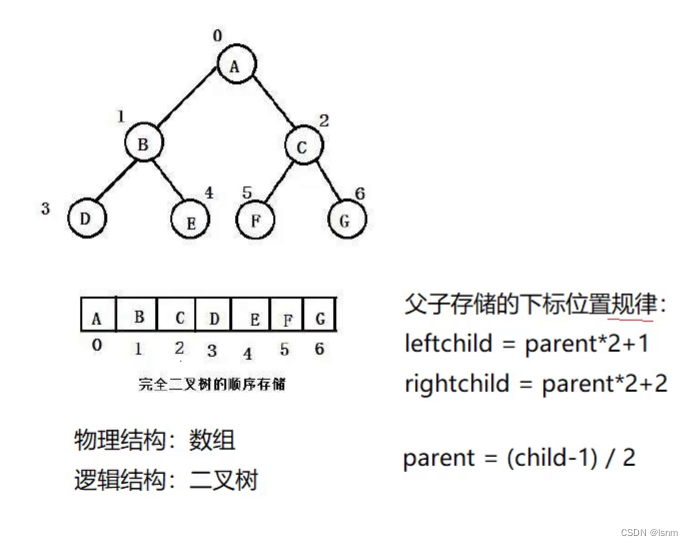
由于右孩子都是偶数,所以-1之后除以二,可以消除小数点的影响。如对于E和D,
(4-1)/2=1(1.5),(3-1)/2=1,D和E就都能找到父亲了。
想利用数组找回二叉树也很容易,按照数量1 2 4 8....的顺序拿数据拼接即可
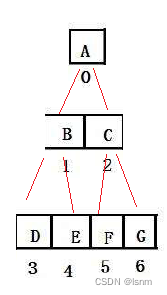
那能否利用数组存储其他类型的树呢?
先说结论,数组只适合满二叉树和完全二叉树 ,否则就如下图,会造成大量空间的浪费
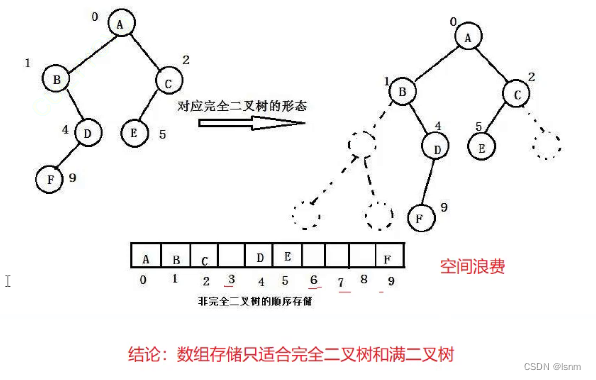
其余普通的更适合二叉链
(根为第一层,不从第零层开始计数,但是编号是根一般编为0号,便于和数组下标对接,这一点很容易混淆,望注意)
4.堆(Heap)
4.1堆概念
(请勿将数据结构中的堆与操作系统中的堆概念混淆,仅仅是名字相同而已)
堆必须是一个完全二叉树,分为大堆和小堆(也叫大根堆和小根堆)。
小堆(任何一个父亲<=孩子)
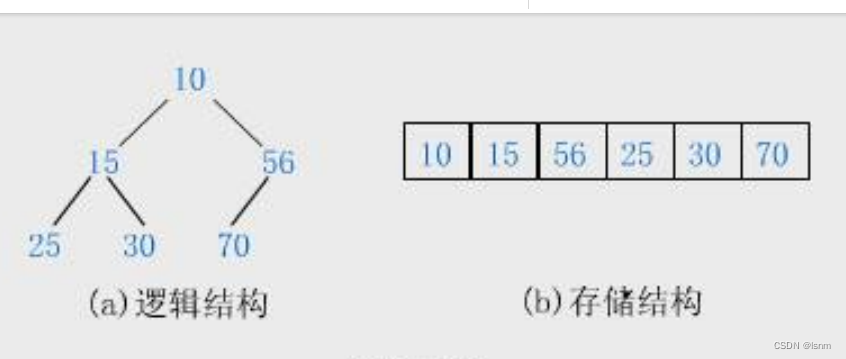
大堆(任何一个父亲>=孩子)

小根堆可用于找最小值,大根堆可用于找最大值
但注意:没有规定兄弟之间的大小关系(也就是叔侄之间没有确定的大小关系),当然,爷孙之间肯定也有大小关系
“只有搜索二叉树规定了左右兄弟的大小![]() ”
”
4.2实现堆的基本结构和接口
基于上文,我们用顺序表为物理结构,构建堆(以小堆为例,根为最小)
typedef int HeapDataType;
typedef struct Heap {
HeapDataType* arr;
int size;
int capacity;
}HP;
4.2.1 HPPush
不管是对于一个空堆,还是已经形成的堆,新插入的数据第一步只需要很简单的先加入顺序表。尾差在数组尾巴,空间不够(size==capacity)就扩容
但是假若插入的数据较小,已经大于他此时的父辈了呢?
利用向上调整算法:插入数据后和父亲比,比父亲小就和父亲交换。
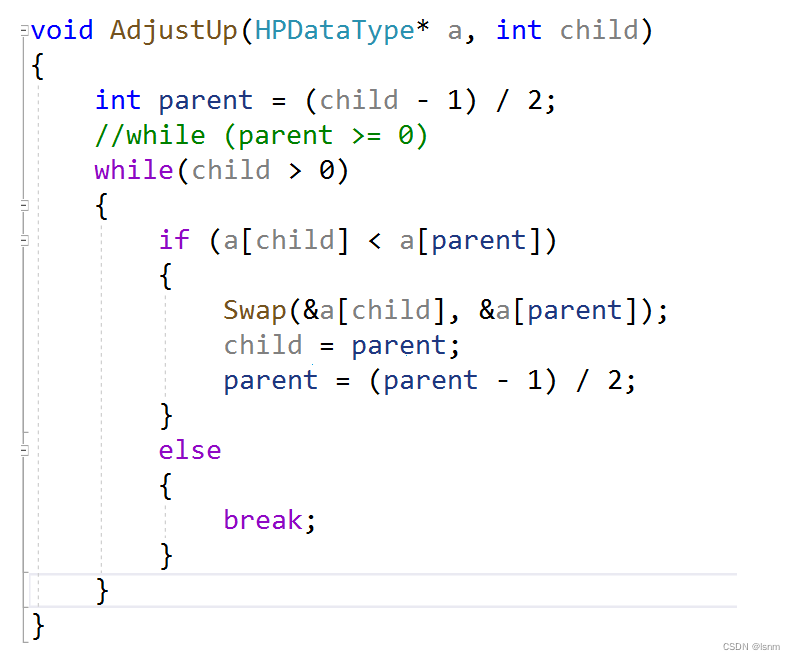
先进入数组,从child找到parent的下标(由于child是大于等于0的整数,所以parent一定大于等于0),若child更下,就封装一个交换函数,交换child和parent的值,再找到新的child和parent.
如果child已经交换到下标为0的位置了,child已经和parent一起作为根了(并不影响,已达成我们的目的),可以跳出循环了。
实现如下
void Swap(HeapDataType* p1, HeapDataType* p2) {
assert(p1 && p2);
HeapDataType tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void AdJustUp(HeapDataType* arr, int child) {
int parent = (child - 1) / 2;
while (child>0) {
if (arr[child] < arr[parent]) {
Swap(&arr[child], &arr[parent]);
child = parent;
parent = (parent - 1) / 2;
}
else {
break;
}
}
}
void HPPush(HP* php, HeapDataType x) {
assert(php);
//不够就扩容
if (php->capacity == php->size) {
int newcapacity = php->size == 0 ? 4 : 2 * php->capacity;
HeapDataType* tmp = (HeapDataType*)realloc(php->arr, newcapacity * sizeof(HeapDataType));
if (tmp == NULL) {
perror("realloc fail");
exit(1);
}
php->arr = tmp;
php->capacity = newcapacity;
}
php->arr[php->size] = x;
php->size++;
//向上调整算法
AdJustUp(php->arr, php->size - 1);
}(整个树的形状与结构应该一直在你的脑海中)
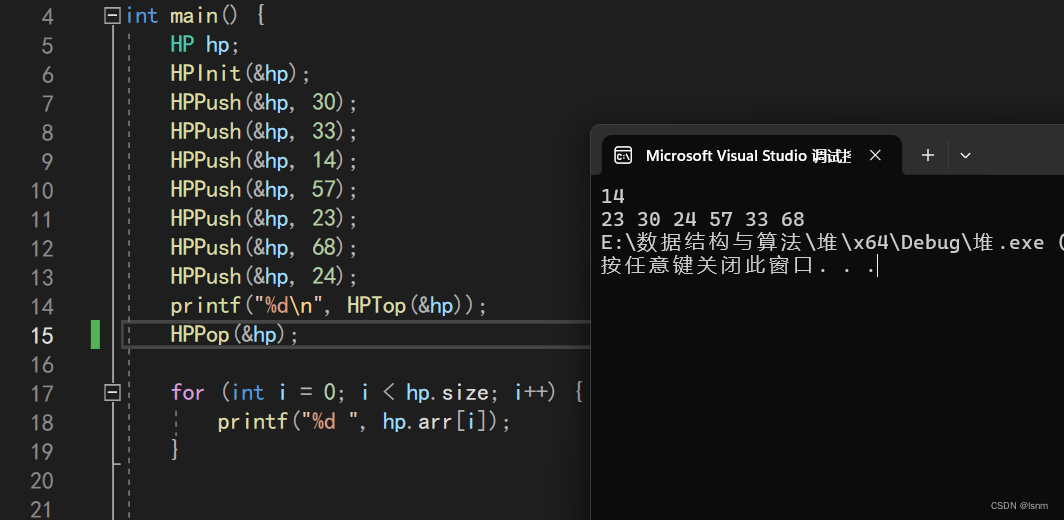
我们对push操作进行测试:
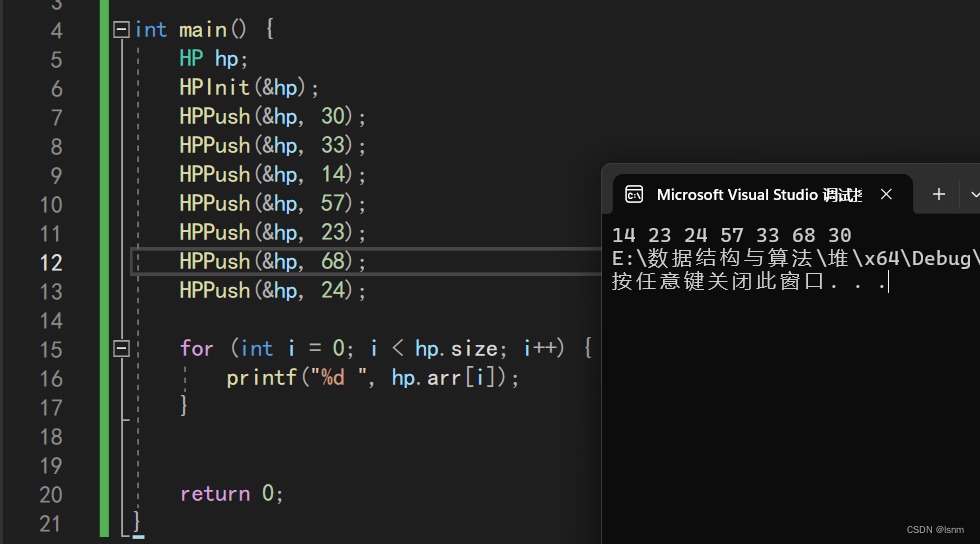
现在,只要经过Push操作进堆,所有数据都满足小堆的排列规则。
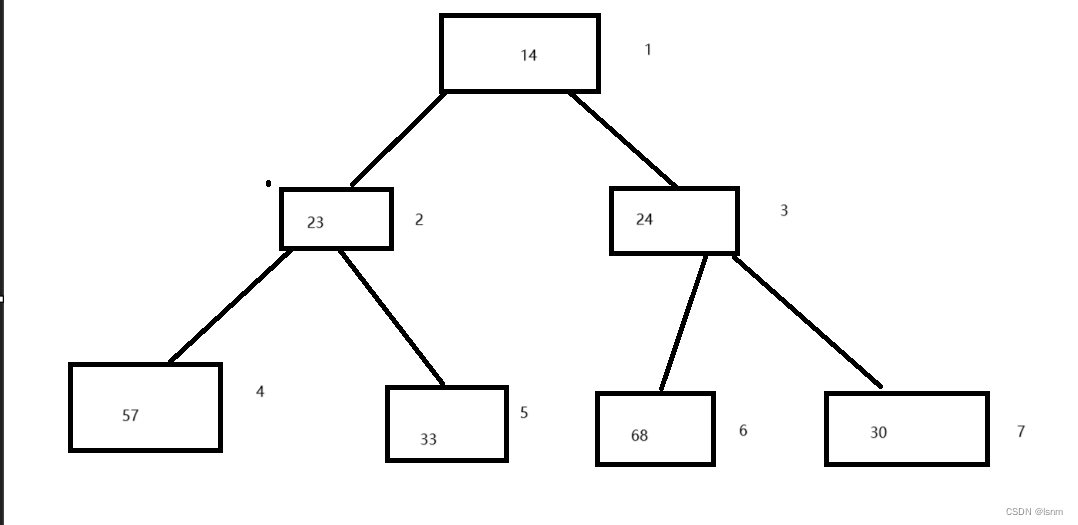
一些其他用例:
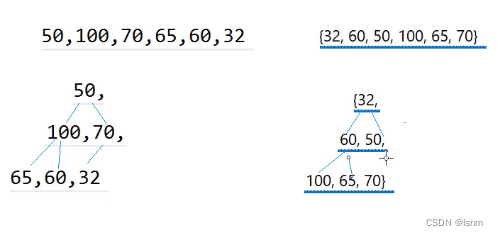
将一个数组使用堆插入后,他都会直接变成期望的堆————原因就在于插入时有向上调整算法,每插入一个就会根据大小而改变位置
4.2.2HeapTop与HeapPop
HeapTop ——取堆顶,也就是根,小堆就是取最小值,大堆就是取最大值
直接返回arr[0]即可。
HeapPop——规定,删除是删除堆顶的数据
如果直接将下标为1的数据往前挪动,能行吗?

显然不能通过。
于是,计算机的先辈们发明了这样一种方法:
1.首先交换首位数据arr[size-1]和arr[0]
2.再删除尾数据
3.最后进行向下调整算法(让不合规的根走到叶子的位置去)
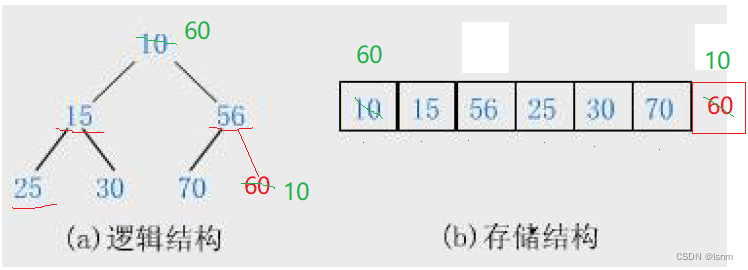
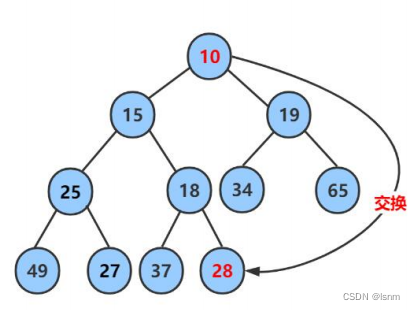
向下调整算法:
任意两个亲兄弟,右孩子的下标都是左孩子+1(没有其他特殊情况,+1不可能到下一辈,因为没有右孩子的位置一定是末位置)
不论是往左还是往右,我们一直在寻找更小的那一个数。所以我们利用假设法,找到左右孩子中更小的那个,进行交换操作,并且迭代。
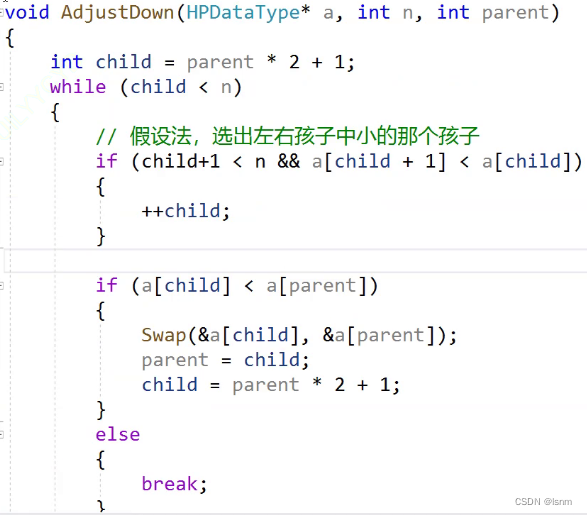
每一轮结束后都将child走到新的左孩子的位置,并且由于完全二叉树的定义,不存在child+1就走到其他亲戚处的可能性(唯一的可能性是退化成下图中的树形,但是此时child+1必定是大于child的),更何况这不是一个完全二叉树。
代码实现:
void AdjustDown(HP* php) {//建议还是将参数设置为上图的参数,便于复用
int parent = 0;
int child = parent * 2 + 1;
//int smaller = leftchild;
//开始假设法找小
while (child<php->size) {
//smaller = leftchild;
if (php->arr[child] > php->arr[child+1]) {
child ++;
}
//已经找到小,向下调整
if (php->arr[parent] > php->arr[child]) {
Swap(&php->arr[parent], &php->arr[child]);
parent = child;
child = parent * 2 + 1;
}
else {
break;
}
}
}
void HPPop(HP* php) {
assert(php);
Swap(&php->arr[0], &php->arr[php->size - 1]);
php->size--;
//向下调整算法
AdjustDown(php);
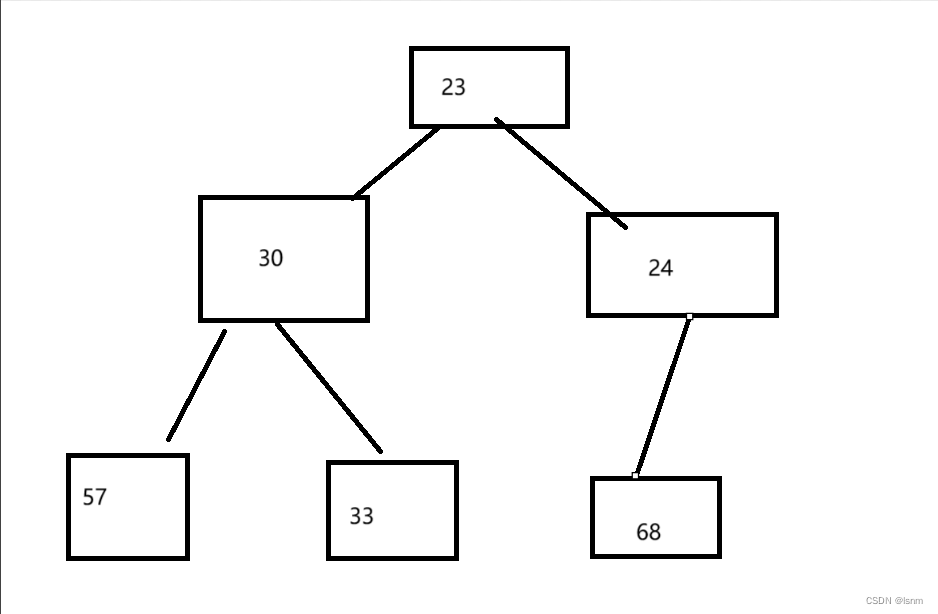
}我们先打印出堆顶数据(此时的堆结构如前文中push后的结构,再pop掉最小的14)
新的、由6个数据构成的新的小堆就完成了。
4.2.3HeapEmpty
直接返回size是否等于0即可
bool HPEmpty(HP* php) {
return php->size == 0;
}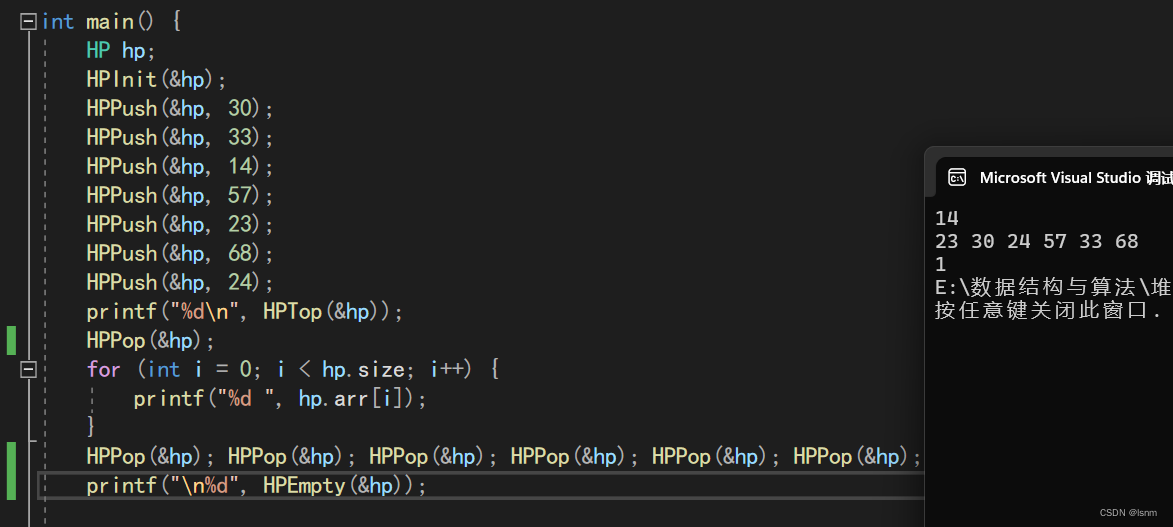
(进行测试功能是可以直接复制粘贴,只要完成目标就行,此时不太需要考虑精简代码 )
到此为止,希望认真学明白的同学建议先独立实现以上接口,再接着阅读
4.3 效率分析与优化(重点)
1.堆的层数和数量关系
回头看我们的堆,完全二叉树都有如下规律:

(满二叉树是完全二叉树的特殊形式)

对于任意h层的完全二叉树,其节点个数就在2^(h-1)~2^h - 1之间。现在我们知道,在之后的时间复杂度计算中,h大概的数值在logN左右(默认省略了底数2)。
2.前文操作的时间复杂度
push和pop的时间复杂度都是O(logn),远远优于O(n)(刚刚的移动数组就是O(n))

而push、pop的建堆的时间复杂度就是AdJustUp 和 AdJustDown的时间复杂度 。
我们虽然实现了堆的各个接口,但是我们前文中想要push操作就只能一次一次写,而真实的运用情况应该是给了你很多数据(比方给了你一个数组),你希望将这些数据用堆的方式来管理,这个时候如果依然按照前文中 ,先初始化一个堆,再利用循环一次一次Push(共循环n次),其时间复杂度是O(n*logn)(n次logn的操作),因此我们尝试写一个新的初始化函数,能用堆处理交给我们的数组。
void HPInitArry(HP* php, HeapDataType* a, int n) {
assert(php);
//a数组就是用户给我们的数据
php->arr = (HeapDataType*)malloc(sizeof(HeapDataType) * n);
if (php->arr = NULL) {
perror("malloc fail!");
exit(1);
}
memcpy(php->arr, a, n * sizeof(HeapDataType));
php->capacity = php->size = n;
//至此,我们开辟了一个新的(希望实现成堆的)空间,并且把a数组的内容拷贝了进来。
//接下来想办法将这些拷贝进来的数据实现成堆
}3.向上调整算法和向下调整算法用于建堆
先分析逻辑:
回忆向上调整的逻辑,“我们在本来建立好的堆的末尾(对应的物理结构——数组的末尾)加上新的数据作为新的叶子(child),再依靠公式parent=(child-1)/2 , 来找新叶子的父亲,比较是否需要调整,以此类推,最坏情况可能需要调整到根部 ”
那么,对于我们已经建立好的但是没有符合数据规律的堆,我们先跳过根部(第1层),
从第二层的第一个元素(数组下标为1)开始,每个元素都进行一次向上调整。这样,每次向上调整之前,要调整的数据之上的数据都是已经调整好的、满足条件的堆的排布。

晃眼一看,每次AdJustUp的复杂度为log n,一共调整(n-1)次,那时间复杂度不就是O(n* logn)吗?

“华生,你没有发现忙点 ”
错误的,只有在最后一层才调整logn, 其余时候,在第几层就调整几次,,,,,
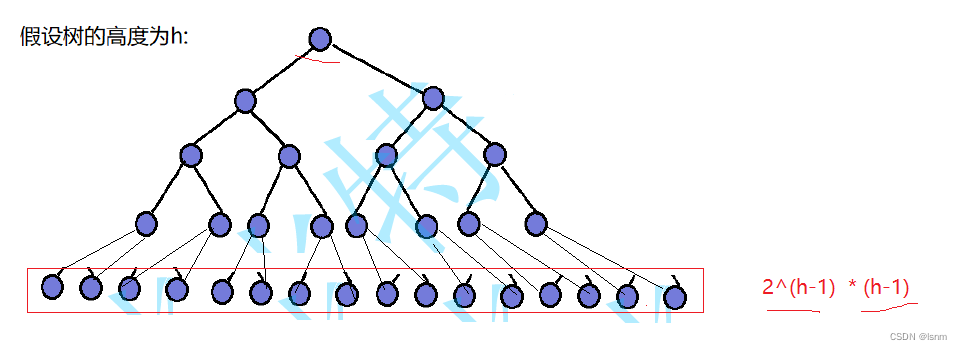
所以整体的调整次数应该是:

(在第h层,其调整次数就是h-1,但是每一层需要调整的数量都是上一层的两倍)
这是一个高中经典的等差+等比数列求和问题,解法大致为让F(h)左端乘以公比为二式,再让原式与二式作差即可,此处不多赘述。结果如下:
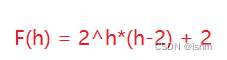
我们将h按照N最大的情况进行换算可得,
需要的总次数=![]()
所以时间复杂度也就是O(nlogn).
我把这种方法称之为“向下遍历的向上调整算法”
void HPInitArry(HP* php, HeapDataType* a, int n) {
assert(php);
//a数组就是用户给我们的数据
php->arr = (HeapDataType*)malloc(sizeof(HeapDataType) * n);
if (php->arr = NULL) {
perror("malloc fail!");
exit(1);
}
memcpy(php->arr, a, n * sizeof(HeapDataType));
php->capacity = php->size = n;
//至此,我们开辟了一个新的(希望实现成堆的)空间,并且把a数组的内容拷贝了进来。
//接下来想办法将这些拷贝进来的数据实现成堆
//1.先使用向下遍历的向上调整算法
for (int i = 1; i < php->size; i++) {
AdJustUp(php->arr, i);
}
}向上遍历的向下调整:
同理可得:从倒数第二层开始,每一层都向下调一次,调整完一个数据就--,继续调整上一个数据。

//2.使用向上遍历的向下调整算法
for (int i = (php->size - 1 - 1) / 2; i > 0; i--) {
AdjustDown(php->arr, php->size,i);
}ps:php->size-1是最后一个元素的下标,也就是child,(child-1)/2才是我们希望找到的倒数第二排的父亲。
同样的计算方法,最后计算出来答案是O(n).
为什么在建堆时,“向上遍历的向下调整”优于“向下增加的向上调整”呢?
因为向下调整直接跳过了个数几乎占一半的叶子辈分,需要排序的数据量几乎少一半
而向上调整只跳过了个数为1的根辈分,基本上等于没有跳过。
4.4堆排序简介
我们现在已经将客户给的数组数据进行堆化了,接下来我们依靠堆化的数据实现经典的堆排序。
假设我们此时希望升序排列,那就应当使用小根堆,然后依次top再pop.
但是,当我们花了那么多心思写完了整个堆,再top和pop,此时的复杂度为前面的造轮子O(n)+O(n),取为O(n),这样的整体代码成本是不是太高了?
综上所述,与其使用向上调整建堆,还不如使用快速排序(也是nlogn)直接对数组进行排序。
此时我们构建整个堆没有任何时间优势。
那么,能否不造轮子呢???
直接对客户给我们的数组a使用向上遍历的向下调整算法,获得数组{0,3,1,4,6,9,2,7,5,8}
假设我们希望获得升序的排列,那么应该将调整算法改为大根堆还是小根堆呢?
按照上面的思路,为了从小到大一个一个拿出我们希望的数据,应该是使用小根堆,来康康效果:

向上向下调整的基础都是:“前进”的方向本身已经形成了符合规定的堆
如上图,建小根堆之后,我们拿出最小的数据,剩下的数据关系一乱,就不能使用向下调整,只能重新建堆,时间成本就高了(应该在O(
))。而重新建堆之后,每建一次堆,都只能选出一个最小的数,比冒泡排序还慢。
接下来就是变魔术的时刻了,我们聪明的前辈们想出了这样一个方法:
升序用大堆,降序用小堆。(不用实现轮子,但是得实现向下调整算法)
以升序为例:
我们先造出大根堆{9 8 3 7 8 1 2 5 4 0},根(也就是9)一定是最大的数字,让其与较小的0互换位置,并且size--,让9留在数组中但是不再对9进行任何调整的处理,让它置身于事外。再让0做向下调整算法,让除9之外次大的数字坐到根的位置上。

其本质与HPPop是一个道理,只是让希望删除的数据留在数组末尾。
由于前文的实现都是小根堆,所以我们此处实现降序:
创建堆的时间复杂度是O(N),类似于pop的堆排序算法的时间复杂度是:
也就是
![]()
约等于nlogn .
至此,我们的堆排序算法简介就到此。