题目

红色和紫色

博弈论，想得出来思路就简单，想不出来就难。一般使用猜测法。

思路

如果小红随意取一个格子涂色，那么小紫怎么涂色才是她的最优选择呢？

假设小紫只能选择小红涂色的格子的相邻格子或者是最近斜对角的一个格子涂色，这两种方案中哪种才是小紫的最优选择呢？不难发现，小紫应该选择和小红相邻的格子涂色。

为什么就不难发现呢？

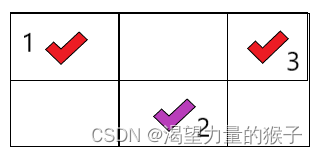
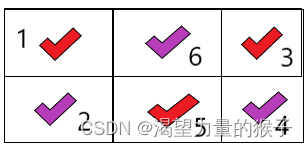
反例：如果给出一个2行3列的网格，小紫选择斜角会输，而选择相邻格子会赢。
选择斜角格子，小紫输：

选择相邻格子，小紫赢：

根据以上假设，我们似乎有点感觉了，并得到以下猜想：

• 如果网格数为偶数，那么小紫赢，因为不管小红如何涂色，小紫总能在其相邻的格子涂色，并且小红不能给红色格子的相邻格子涂色，这意味着无论如何小紫总能在小红涂色的格子的相邻位置找到一个能涂色的格子。
• 反之，如果网格数为奇数，那么小红赢。

那么就判断格子总数是否是奇数即可。

但是题目所给的数据很大，如果想直接相乘的话要使用长整型过渡。

使用长整型也装不下怎么办呢？

我们知道，两个奇数相乘是奇数，两个偶数相乘是偶数，一个奇数一个偶数相乘是偶数，由此即可直接判断。

代码

#include <iostream>
using namespace std;

// 使用位运算判断奇偶性
bool can_win(int a, int b) { return a & b & 1; }

int main(void) {
    int n = 0, m = 0;
    cin >> n >> m;
    cout << (can_win(n, m) ? "akai" : "yukari") << endl;
    return 0;
}