探索数据结构：双向链表的灵活优势

news2024/9/23 1:38:23


✨✨ 欢迎大家来到贝蒂大讲堂✨✨

🎈🎈养成好习惯，先赞后看哦~🎈🎈

所属专栏：数据结构与算法
贝蒂的主页：Betty’s blog

1. 前言

前面我们学习了单链表，它解决了顺序表中插入删除需要挪动大量数据的缺点。但同时也有仍需改进的地方，比如说：我们有时候需要寻找某个节点的前一个节点，对于单链表而言只能遍历，这样就可能造成大量时间的浪费。为了解决这个问题，我们就要学习今天的主角——带头双向循环链表。

2. 双向链表的功能

  1. 初始化顺序表中的数据。
  2. 对顺序表进行尾插(末尾插入数据)。
  3. 对顺序表进行头插(开头插入数据)。
  4. 对顺序表进行头删(开头删除数据)。
  5. 对顺序表进行尾删(末尾删除数据)。
  6. 对顺序表就像查找数据。
  7. 对顺序表数据进行修改。
  8. 任意位置的删除和插入数据。
  9. 打印顺序表中的数据。
  10. 销毁顺序表。

3. 双向链表的定义

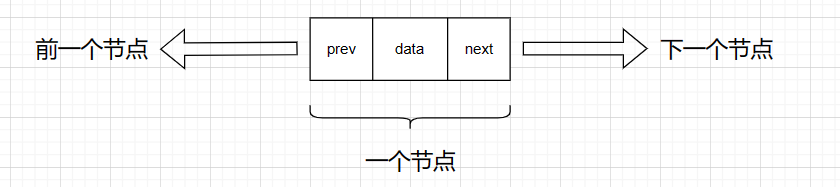
双向链表的定义结构体需要包含三个成员，一个成员存储数值，一个成员存储前一个节点的地址，最后一个成员存储下一个节点的地址。

typedef int LTDataType;
typedef struct DoubleList
{
	struct DoubleList* prev;//指向前一个节点
	LTDataType data;
	struct DoubleList* next;//指向下一个节点
}DListNode;

4. 双向链表的功能

4.1 初始化双向链表

在初始化双向链表时，我们需要创建一个头节点，也就是我们常说的哨兵位头节点。

(1) 创建头结点
DListNode* DLNodeCreat(LTDataType x)
{
	DListNode* newnode = (DListNode*)malloc(sizeof(DListNode));
	if (newnode == NULL)
	{
		perror("malloc fail:");
		return NULL;
	}
	newnode->prev = NULL;
	newnode->next = NULL;
	newnode->data = x;
	return newnode;
}
(2) 初始化

初始化将头节点的前后指针都指向自己，并将数值至为-1。

DListNode* InitDList()
{
	DListNode* phead = DLNodeCreat(-1);
	phead->prev = phead;
	phead->next = phead;
	return phead;
}
(3) 复杂度分析
  • 时间复杂度：没有其他额外的时间消耗，时间复杂度为O(1)。
  • 空间复杂度：固定创造一个节点，空间复杂度为O(1)。

4.2 双向链表尾插

因为我们实现的双向链表存在头节点，所以我们不需要像实现单链表一样先判断链表是否为空。

(1) 代码实现
void DListPushBack(DListNode* ptr, LTDataType x)
{
	assert(ptr);
	DListNode* tail = ptr->prev;
	DListNode* newnode = DLNodeCreat(x);
	tail->next = newnode;
	newnode->prev = tail;
	ptr->prev = newnode;
	newnode->next = ptr;
}
(2) 复杂度分析
  • 时间复杂度：没有其他额外的时间消耗，时间复杂度为O(1)。
  • 空间复杂度：固定创造一个节点，空间复杂度为O(1)。

4.3 双向链表头插

因为带头双向循环链表的特性，即使只有头节点进行头插，代码实现也是相同的。

(1) 代码实现
void DListPushFront(DListNode* ptr, LTDataType x)
{
	assert(ptr);
	DListNode* next = ptr->next;
	DListNode* newnode = DLNodeCreat(x);
	ptr->next = newnode;
	newnode->prev =ptr;
	newnode->next = next;
	next->prev = newnode;
}
(2) 复杂度分析
  • 时间复杂度：没有其他额外的时间消耗，时间复杂度为O(1)。
  • 空间复杂度：固定创造一个节点，空间复杂度为O(1)。

4.4 双向链表尾删

有了循环找尾节点也十分容易，双向链表尾删自然并不困难。但是需要防止删除头节点。

(1) 代码实现
void DListPopBack(DListNode* ptr)
{
	assert(ptr);
	assert(ptr->next != ptr);//放置删除头节点
	DListNode* tail = ptr->prev;
	DListNode* tailprev = tail->prev;
	free(tail);
	tail == NULL;
	tailprev->next = ptr;
	ptr->prev = tailprev;
}
(2) 复杂度分析
  • 时间复杂度：没有其他额外的时间消耗，时间复杂度为O(1)。
  • 空间复杂度：没有额外的空间消耗，空间复杂度为O(1)。

4.5 双向链表头删

头删与尾删一样，都需要防止删除头节点。

(1) 代码实现
void DListPopFront(DListNode* ptr)
{
	assert(ptr);
	assert(ptr->next != ptr);
	DListNode* phead = ptr->next;
	DListNode* pheadnext = phead->next;
	free(phead);
	ptr->next = pheadnext;
	pheadnext->prev = ptr;
}
(2) 复杂度分析
  • 时间复杂度：没有其他额外的时间消耗，时间复杂度为O(1)。
  • 空间复杂度：没有额外的空间消耗，空间复杂度为O(1)。

4.6 双向链表查找

和单链表一样，我们也可以对双向链表进行查找。如果找到就返回该节点的地址，否则返回NULL。

(1) 代码实现
DListNode* DListFind(DListNode* ptr, LTDataType x)
{
	assert(ptr);
	DListNode* cur = ptr->next;
	while (cur != ptr)
	{
		if (cur->data == x)
		{
			return cur;
		}
		cur = cur->next;
	}
	return NULL;
}
(2) 复杂度分析
  • 时间复杂度：可能需要遍历整个链表，时间复杂度为O(N)。
  • 空间复杂度：没有额外的空间消耗，空间复杂度为O(1)。

4.7 修改双向链表

我们可以结合双向链表的查找，对双向链表进行修改。

(1) 代码实现
void DListModify(DListNode* ptr, DListNode* pos, LTDataType x)
{
	assert(ptr);
	assert(ptr != pos);//防止对头节点操作
	DListNode* cur = ptr->next;
	while (cur != ptr)
	{
		if (cur == pos)
		{
			cur->data = x;
		}
		cur = cur->next;
	}
}
(2) 复杂度分析
  • 时间复杂度：可能需要遍历整个链表，时间复杂度为O(N)。
  • 空间复杂度：没有额外的空间消耗，空间复杂度为O(1)。

4.8 双向链表指定插入数据

随机插入数据可以分为：向前插入与向后插入。

(1) 向前插入
void DListInsertF(DListNode* ptr, DListNode* pos, LTDataType x)
{
	assert(ptr);
	DListNode* newnode = DLNodeCreat(x);
	DListNode* prev = pos->prev;
	newnode->prev = prev;
	newnode->next = pos;
	prev->next = newnode;
	pos->prev = newnode;
}
(2) 向后插入
void DListInsertB(DListNode* ptr, DListNode* pos, LTDataType x)
{
	assert(ptr);
	DListNode* newnode = DLNodeCreat(x);
	DListNode* next = pos->next;
	newnode->prev = pos;
	newnode->next = next;
	next->prev = newnode;
	pos->next = newnode;
}
(3) 复杂度分析
  • 时间复杂度：没有其他额外的时间消耗，时间复杂度为O(1)。
  • 空间复杂度：没有额外的空间消耗，空间复杂度为O(1)。

4.9 指定位置删除数据

任意删除也需要放置删除头节点，并且因为其特点只需要一个参数就能完成该操作。

(1) 代码实现
void DListErase(DListNode* pos)
{
	assert(pos);
	assert(pos != pos->next);
	pos->prev->next = pos -> next;
	pos->next->prev = pos->prev;
	free(pos);
	pos = NULL;
}
(2) 复杂度分析
  • 时间复杂度：没有其他额外的时间消耗，时间复杂度为O(1)。
  • 空间复杂度：没有额外的空间消耗，空间复杂度为O(1)。

4.10 打印双向链表

打印双向链表只需将循环之前的数据全部打印即可。

(1) 代码实现
void DLTPrint(DListNode* ptr)
{
	assert(ptr);
	printf("guard");
	DListNode* cur = ptr->next;
	while (cur != ptr)
	{
		printf("<==>%d", cur->data);
		cur = cur->next;
	}
	printf("\n");
}
(2) 复杂度分析
  • 时间复杂度：没有其他额外的时间消耗，时间复杂度为O(1)。
  • 空间复杂度：没有额外的空间消耗，空间复杂度为O(1)。

4.11 销毁双向链表

(1) 代码实现
void DListDestroy(DListNode* ptr)
{
	assert(ptr);
	DListNode* cur = ptr->next;
	while (cur != ptr)
	{
		DListNode* next = cur->next;
		free(cur);
		cur = next;
	}
	free(ptr);
}
(2) 复杂度分析
  • 时间复杂度：没有其他额外的时间消耗，时间复杂度为O(1)。
  • 空间复杂度：没有额外的空间消耗，空间复杂度为O(1)。

5. 完整代码

5.1 DList.h

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
typedef int LTDataType;
typedef struct DoubleList
{
	struct DoubleList* prev;//指向前一个节点
	LTDataType data;
	struct DoubleList* next;//指向下一个节点
}DListNode;
DListNode* InitDList();//初始化
void DListPushBack(DListNode* ptr, LTDataType x);//尾插
void DLTPrint(DListNode* ptr);//打印
void DListPushFront(DListNode* ptr, LTDataType x);//头插
void DListPopBack(DListNode* ptr);//尾删
void DListPopFront(DListNode* ptr);//头删
DListNode*DListFind(DListNode* ptr, LTDataType x);//查找
void DListModify(DListNode* ptr, DListNode* pos);//修改
void DListInsertF(DListNode* ptr, DListNode* pos, LTDataType x);//任意位置之前插入
void DListInsertB(DListNode* ptr, DListNode* pos, LTDataType x);//任意位置之后插入
void DListErase(DListNode* pos);//任意位置删除
void DListDestroy(DListNode* ptr);//销毁双向链表

5.2 DList.c

#include"DoubleList.h"
DListNode* DLNodeCreat(LTDataType x)
{
	DListNode* newnode = (DListNode*)malloc(sizeof(DListNode));
	if (newnode == NULL)
	{
		perror("malloc fail:");
		return NULL;
	}
	newnode->prev = NULL;
	newnode->next = NULL;
	newnode->data = x;
	return newnode;
}
DListNode* InitDList()
{
	DListNode* phead = DLNodeCreat(-1);
	phead->prev = phead;
	phead->next = phead;
	return phead;
}
void DListPushBack(DListNode* ptr, LTDataType x)
{
	assert(ptr);
	DListNode* tail = ptr->prev;
	DListNode* newnode = DLNodeCreat(x);
	tail->next = newnode;
	newnode->prev = tail;
	ptr->prev = newnode;
	newnode->next = ptr;
}
void DListPushFront(DListNode* ptr, LTDataType x)
{
	assert(ptr);
	DListNode* next = ptr->next;
	DListNode* newnode = DLNodeCreat(x);
	ptr->next = newnode;
	newnode->prev =ptr;
	newnode->next = next;
	next->prev = newnode;
}
void DListPopBack(DListNode* ptr)
{
	assert(ptr);
	assert(ptr->next != ptr);//放置删除头节点
	DListNode* tail = ptr->prev;
	DListNode* tailprev = tail->prev;
	free(tail);
	tail == NULL;
	tailprev->next = ptr;
	ptr->prev = tailprev;
}
void DListPopFront(DListNode* ptr)
{
	assert(ptr);
	assert(ptr->next != ptr);
	DListNode* phead = ptr->next;
	DListNode* pheadnext = phead->next;
	free(phead);
	ptr->next = pheadnext;
	pheadnext->prev = ptr;
}
DListNode* DListFind(DListNode* ptr, LTDataType x)
{
	assert(ptr);
	DListNode* cur = ptr->next;
	while (cur != ptr)
	{
		if (cur->data == x)
		{
			return cur;
		}
		cur = cur->next;
	}
	return NULL;
}
void DListModify(DListNode* ptr, DListNode* pos, LTDataType x)
{
	assert(ptr);
	assert(ptr != pos);//防止对头节点操作
	DListNode* cur = ptr->next;
	while (cur != ptr)
	{
		if (cur == pos)
		{
			cur->data = x;
		}
		cur = cur->next;
	}
}
void DListInsertF(DListNode* ptr, DListNode* pos, LTDataType x)
{
	assert(ptr);
	DListNode* newnode = DLNodeCreat(x);
	DListNode* prev = pos->prev;
	newnode->prev = prev;
	newnode->next = pos;
	prev->next = newnode;
	pos->prev = newnode;
}
void DListInsertB(DListNode* ptr, DListNode* pos, LTDataType x)
{
	assert(ptr);
	DListNode* newnode = DLNodeCreat(x);
	DListNode* next = pos->next;
	newnode->prev = pos;
	newnode->next = next;
	next->prev = newnode;
	pos->next = newnode;
}
void DListErase(DListNode* pos)
{
	assert(pos);
	assert(pos != pos->next);
	pos->prev->next = pos -> next;
	pos->next->prev = pos->prev;
	free(pos);
	pos = NULL;
}
void DLTPrint(DListNode* ptr)
{
	assert(ptr);
	printf("guard");
	DListNode* cur = ptr->next;
	while (cur != ptr)
	{
		printf("<==>%d", cur->data);
		cur = cur->next;
	}
	printf("\n");
}
void DListDestroy(DListNode* ptr)
{
	assert(ptr);
	DListNode* cur = ptr->next;
	while (cur != ptr)
	{
		DListNode* next = cur->next;
		free(cur);
		cur = next;
	}
	free(ptr);
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1518474.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

IM项目题

IM项目题

消息的可靠性 前言 IM系统的可靠性指的是端到端的可靠性&#xff0c;并不是tcp的可靠性&#xff0c;它是指客户端A&#xff0c;客户端B以及服务端三端通信之间的可靠性&#xff0c;并不是客户端A到服务端这么一个上行消息的可靠&#xff0c;这个tcp就可以保证了&#xff0c;当…
阅读更多...
openssl3.2 - note - Getting Started with OpenSSL

openssl3.2 - note - Getting Started with OpenSSL

文章目录 openssl3.2 - note - Getting Started with OpenSSL概述笔记openssl 历史版本Configure 选项开关支持的OSopenssl 文档简介安装新闻每个平台的安装文档支持的命令列表配置文件格式环境变量 END openssl3.2 - note - Getting Started with OpenSSL 概述 看到官方文档…
阅读更多...
基于单片机的智能环境监测系统

基于单片机的智能环境监测系统

摘 要 本设计主要由温湿度检测、烟雾检测电路、报警电路、显示电路和人体检测等模块组成。温湿度检测部分使用的是DHT11这种型号的温湿度传感器。DHT11是一种单总线型数字式温湿度传感器&#xff0c;它具有误差小、分辨率高、抗干扰能力强等特点。在烟雾检测电路模块当中&…
阅读更多...
ant-design的DatePicker、a-range-picker限制选择今天之前的时间和今天之后的日期时间

ant-design的DatePicker、a-range-picker限制选择今天之前的时间和今天之后的日期时间

a-range-picker限制选择今天之前的时间和今天之后的时间 antd的时间选择器做限制主要用到的参数是disabledDate &#xff0c;下面我们看下案例&#xff1a; HTML&#xff1a; <a-date-picker :disabledDate"disabledDate"></a-date-picker> //最简单…
阅读更多...
Linux学习之网络

Linux学习之网络

目录 认识协议 网络协议初始 协议分层 OSI七层模型 TCP/IP的四层模型 数据包封装和分用 以太网通信 ip地址与MAC地址 网络编程套接字 端口号&#xff08;port&#xff09; 认识协议 网络字节序 socket接口 网络的产生是计算机历史的必然性&#xff0c;是计算机发展…
阅读更多...
【AI+CAD】（二）LLM和VLM生成结构化数据结构(PPT/CAD/DXF)

【AI+CAD】（二）LLM和VLM生成结构化数据结构(PPT/CAD/DXF)

当前LLM和VLM在PPT生成任务上已经小有成效，如ChatPPT。 @TOC 1. PPT-LLM LLM根据用户的instruction生成规范的绘制ppt的API语句：即使是最强的GPT-4 + CoT也只能达到20-30%的内容准确度。 LLM输入：User_instruction(当前+过去)、PPT_content、PPT_reader_API。其中 PPT_rea…
阅读更多...
文心一言 VS 讯飞星火 VS chatgpt （215）-- 算法导论16.2 2题

文心一言 VS 讯飞星火 VS chatgpt （215）-- 算法导论16.2 2题

二、设计动态规划算法求解 0-1 背包问题&#xff0c;要求运行时间为 O(nW)&#xff0c;n为商品数量&#xff0c;W是小偷能放进背包的最大商品总重量。如果要写代码&#xff0c;请用go语言。 文心一言&#xff1a; 0-1 背包问题是一个典型的动态规划问题&#xff0c;其目标是在…
阅读更多...
Supervisor，一个超酷的 Python 库！

Supervisor，一个超酷的 Python 库！

大家好&#xff0c;今天为大家分享一个超酷的 Python 库 - supervisor。 Github地址&#xff1a;https://github.com/Supervisor/supervisor 在大型项目中&#xff0c;经常需要管理多个进程&#xff0c;确保它们能够稳定运行并协同工作。Python提供了许多工具和库来帮助实现进…
阅读更多...
使用Minio搭建文件服务器

使用Minio搭建文件服务器

Minio是一个开源的对象存储服务器&#xff0c;可以用来存储和管理大规模的数据。我们可以用它来存储图片或者视频资源。 minio和阿里云&#xff08;腾讯云、百度云等&#xff09;oss对比 托管方式&#xff1a;MinIO 是一个开源的对象存储系统&#xff0c;可以在自己的服务器或…
阅读更多...
记录Mysql主从复制-读写分离原理

记录Mysql主从复制-读写分离原理

在实际生产环境中&#xff0c;一台MySQL服务器同时对数据库读写&#xff0c;往往满足不了高并发的需求&#xff0c;因此我们可以使用主从复制的方式来实现数据同步&#xff0c;再通过读写分离的手段提高MySQL并发负载能力。 MySQL主从复制原理 如图&#xff1a; &#xff08;1…
阅读更多...
C语言例3-18：使用关系表达式的例子

C语言例3-18：使用关系表达式的例子

关系表达式的一般形式&#xff1a; 表达式 关系运算符 表达式 最初代码如下&#xff1a; #include<stdio.h> int main(void) {int i3,j4,k5;float f11.0, f22.1;char c1a, c2d; //a(97) d(100)printf("i>j 的结果为&#xff1a…
阅读更多...
B/S基于云计算的云HIS智慧医院管理系统源码带电子病历编辑器

B/S基于云计算的云HIS智慧医院管理系统源码带电子病历编辑器

目录 一、系统概述 二、开发环境 三、系统功能 1、门诊部分 2、住院部分 3、电子病历 4、药物管理 5、统计报表 6、综合维护 7、运营运维 云HIS系统&#xff1a;病案首页 云his系统源码 SaaS应用 功能易扩 统一对外接口管理 现如今&#xff0c;大数据、云计算、移动…
阅读更多...
中霖教育：考注册会计师报班能提高通过率吗?

中霖教育：考注册会计师报班能提高通过率吗?

CPA考试涵盖了会计、审计、税法及相关的知识,这些知识点不仅繁多而且专业性强&#xff0c;对于自学能力较弱或时间不足的考生来说&#xff0c;有一定的挑战性。在这种情况下&#xff0c;报班提供了系统化和结构化的学习方案&#xff0c;有助于考生更快地掌握考点和难点。 经验…
阅读更多...
分类预测 | Matlab实现GSWOA-KELM混合策略改进的鲸鱼优化算法优化核极限学习机的数据分类预测

分类预测 | Matlab实现GSWOA-KELM混合策略改进的鲸鱼优化算法优化核极限学习机的数据分类预测

分类预测 | Matlab实现GSWOA-KELM混合策略改进的鲸鱼优化算法优化核极限学习机的数据分类预测 目录 分类预测 | Matlab实现GSWOA-KELM混合策略改进的鲸鱼优化算法优化核极限学习机的数据分类预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 GSWOA-KELM分类&#xff0…
阅读更多...
位运算#蓝桥杯

位运算#蓝桥杯

位运算#蓝桥杯 文章目录 位运算#蓝桥杯1、小蓝学位运算2、异或森林3、位移4、笨笨的机器人5、博弈论 1、小蓝学位运算 #include<bits/stdc.h> using namespace std; using LL long long; const LL N 1e97; template<int kcz> struct ModInt { #define T (*this)…
阅读更多...
1997-2022年各省市场化指数及分项指数（初始数据+计算代码+结果）

1997-2022年各省市场化指数及分项指数（初始数据+计算代码+结果）

1997-2022年各省市场化指数及分项指数&#xff08;初始数据计算代码结果&#xff09; 1、时间&#xff1a;1997-2022年 2、来源&#xff1a;2019年之前的数据来源于市场化指数报告&#xff0c;其中2020年之后的数据根据历年数据拓展所得 3、指标&#xff1a;province、year、…
阅读更多...
【办公类-40-01】20240311 用Python将MP4转MP3提取音频 （家长会系列一）

【办公类-40-01】20240311 用Python将MP4转MP3提取音频 （家长会系列一）

作品展示&#xff1a; 背景需求&#xff1a; 马上就要家长会&#xff0c;我负责做会议前的照片滚动PPT&#xff0c;除了大量照片视频&#xff0c;还需要一个时间很长的背景音乐MP3 一、下载“歌曲串烧” 装一个IDM 下载三个“串烧音乐MP4”。 代码展示 家长会背景音乐: 歌曲串…
阅读更多...
Windows 安装 Ubuntu 子系统

Windows 安装 Ubuntu 子系统

大约是22年的时候&#xff0c;开始玩这个windows的子系统&#xff0c;当时安装比较顺利。最近也是想看看linux&#xff0c;就在新电脑上装了个ubuntu&#xff0c;记录安装过程。 1.Microsoft Store 搜索 ubuntu&#xff0c;先看评价&#xff1a;很多报错&#xff0c;先不要慌 2…
阅读更多...
C语言——动态内存分配

C语言——动态内存分配

前言&#xff1a;通过前面的学习&#xff0c;我们知道C语言中在内存中开辟空间的方法有&#xff1a;变量和数组。既然拥有了开辟空间的方法&#xff0c;我们为什么还要学习动态内存分配呢&#xff1f; int val 20; //在内存中开辟四个字节的空间 int arr[10] { 0 }; //在内…
阅读更多...
AI探索实践16 - Typescript开发AI应用8：为大模型增加记忆(Memory)

AI探索实践16 - Typescript开发AI应用8：为大模型增加记忆(Memory)

大家好&#xff0c;我是feng&#xff0c;欢迎关注公众号和我一起探索。如果文章对你有所启发&#xff0c;请为我点赞、转发以及在下方留言自己的理解&#xff01; 每次发文章都看到不少人收藏。我自己也有这个习惯&#xff0c;但是基本上收藏起来的东西都没再打开过。哪怕再遇到…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023