机器学习实战教程（十三）：树回归基础篇

news2025/1/21 15:30:28

一、前言

本篇文章将会讲解CART算法的实现和树的剪枝方法，通过测试不同的数据集，学习CART算法和树剪枝技术。

二、将CART（Classification And Regression Trees）算法用于回归

在之前的文章，我们学习了决策树的原理和代码实现，使用使用决策树进行分类。决策树不断将数据切分成小数据集，直到所有目标标量完全相同，或者数据不能再切分为止。决策树是一种贪心算法，它要在给定时间内做出最佳选择，但不关心能否达到全局最优。

1、ID3算法的弊端

回忆一下，决策树的树构建算法是ID3。ID3的做法是每次选取当前最佳的特征来分割数据，并按照该特征的所有可能取值来切分。也就是说，如果一个特征有4种取值，那么数据将被切分成4份。一旦按某特征切分后，该特征在之后的算法执行过程中将不会再起作用，所以有观点认为这种切分方式过于迅速。

除了切分过于迅速外，ID3算法还存在另一个问题，它不能直接处理连续型特征。只有事先将连续型特征离散化，才能在ID3算法中使用。但这种转换过程会破坏连续型变量的内在特性。

2、CART算法

与ID3算法相反，CART算法正好适用于连续型特征。CART算法使用二元切分法来处理连续型变量。而使用二元切分法则易于对树构建过程进行调整以处理连续型特征。具体的处理方法是：如果特征值大于给定值就走左子树，否则就走右子树。

CART算法有两步：

  • 决策树生成：递归地构建二叉决策树的过程，基于训练数据集生成决策树，生成的决策树要尽量大；自上而下从根开始建立节点，在每个节点处要选择一个最好的属性来分裂，使得子节点中的训练集尽量的纯。不同的算法使用不同的指标来定义"最好"：

  • 决策树剪枝：用验证数据集对已生成的树进行剪枝并选择最优子树，这时损失函数最小作为剪枝的标准。

决策树剪枝我们先不管，我们看下决策树生成。

在决策树的文章中，我们先根据信息熵的计算找到最佳特征切分数据集构建决策树。CART算法的决策树生成也是如此，实现过程如下：

  • 使用CART算法选择特征

  • 根据特征切分数据集合

  • 构建树

3、根据特征切分数据集合

我们先找软柿子捏，CART算法这里涉及到算法，实现起来复杂些，我们先挑个简单的，即根据特征切分数据集合。编写代码如下：

# -*- coding:utf-8 -*-
import numpy as np


def binSplitDataSet(dataSet, feature, value):
    """
    函数说明:根据特征切分数据集合
    Parameters:
        dataSet - 数据集合
        feature - 带切分的特征
        value - 该特征的值
    Returns:
        mat0 - 切分的数据集合0
        mat1 - 切分的数据集合1
    """
    mat0 = dataSet[np.nonzero(dataSet[:, feature] > value)[0], :]
    mat1 = dataSet[np.nonzero(dataSet[:, feature] <= value)[0], :]
    return mat0, mat1


if __name__ == '__main__':
    testMat = np.mat(np.eye(4))
    mat0, mat1 = binSplitDataSet(testMat, 1, 0.5)
    print('原始集合:\n', testMat)
    print('mat0:\n', mat0)
    print('mat1:\n', mat1)

运行结果如下图所示：

我们先创建一个单位矩阵，然后根据切分规则，对数据矩阵进行切分。可以看到binSplitDataSet函数根据特定规则，对数据矩阵进行切分。

现在OK了，我们已经可以根据特征和特征值对数据进行切分了，mat0存放的是大于指定特征值的矩阵，mat1存放的是小于指定特征值的矩阵。接下来，我们就看看如何使用CART算法选择最佳分类特征。

4、CART算法

假设X与Y分别为输入和输出变量，并且Y是连续变量，给定训练数据集：

其中，D表示整个数据集合，n为特征数。

一个回归树对应着输入空间（即特征空间）的一个划分以及在划分的单元上的输出值。假设已将输入空间划分为M个单元R1,R2,...Rm，并且在每个单元Rm上有一个固定的输出值Cm，于是回归树模型可表示为：

这样就可以计算模型输出值与实际值的误差：

我们希望每个单元上的Cm，可以是的这个平方误差最小化。易知，当Cm为相应单元的所有实际值的均值时，可以到最优：

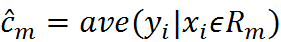
那么如何生成这些单元划分？

假设，我们选择变量 xj 为切分变量，它的取值 s 为切分点，那么就会得到两个区域：

当j和s固定时，我们要找到两个区域的代表值c1，c2使各自区间上的平方差最小：

前面已经知道c1，c2为区间上的平均：

那么对固定的 j 只需要找到最优的s，然后通过遍历所有的变量，我们可以找到最优的j，这样我们就可以得到最优对（j，s），并得到两个区间。

这样的回归树通常称为最小二乘回归树（least squares regression tree）。

上述过程表示的算法步骤为：

除此之外，我们再定义两个参数，tolS和tolN，分别用于控制误差变化限制和切分特征最少样本数。这两个参数的意义是什么呢？就是防止过拟合，提前设置终止条件，实际上是在进行一种所谓的预剪枝（prepruning）操作，在下一小节会进行进一步讲解。

老规矩，先看下我们的测试数据集。

数据集下载地址：数据集下载

如上图所示，数据是2维的。先看下数据的分布情况，编写代码如下：

# -*- coding:utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np


def loadDataSet(fileName):
    """
    函数说明:加载数据
    Parameters:
        fileName - 文件名
    Returns:
        dataMat - 数据矩阵

    """
    dataMat = []
    fr = open(fileName)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        fltLine = list(map(float, curLine))  # 转化为float类型
        dataMat.append(fltLine)
    return dataMat


def plotDataSet(filename):
    """
    函数说明:绘制数据集
    Parameters:
        filename - 文件名
    Returns:
        无

    """
    dataMat = loadDataSet(filename)  # 加载数据集
    n = len(dataMat)  # 数据个数
    xcord = [];
    ycord = []  # 样本点
    for i in range(n):
        xcord.append(dataMat[i][0]);
        ycord.append(dataMat[i][1])  # 样本点
    fig = plt.figure()
    ax = fig.add_subplot(111)  # 添加subplot
    ax.scatter(xcord, ycord, s=20, c='blue', alpha=.5)  # 绘制样本点
    plt.title('DataSet')  # 绘制title
    plt.xlabel('X')
    plt.show()


if __name__ == '__main__':
    filename = 'ex00.txt'
    plotDataSet(filename)

运行结果如下图所示：

可以看到，这是一个很简单的数据集，我们先利用这个数据集测试我们的CART算法。

现在，编写代码如下：

# -*- coding:utf-8 -*-
import numpy as np


def loadDataSet(fileName):
    """
    函数说明:加载数据
    Parameters:
        fileName - 文件名
    Returns:
    
    """
    dataMat = []
    fr = open(fileName)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        fltLine = list(map(float, curLine))  # 转化为float类型
        dataMat.append(fltLine)
    return dataMat


def binSplitDataSet(dataSet, feature, value):
    """
    函数说明:根据特征切分数据集合
    Parameters:
        dataSet - 数据集合
        feature - 带切分的特征
        value - 该特征的值
    Returns:
        mat0 - 切分的数据集合0
        mat1 - 切分的数据集合1

    """
    mat0 = dataSet[np.nonzero(dataSet[:, feature] > value)[0], :]
    mat1 = dataSet[np.nonzero(dataSet[:, feature] <= value)[0], :]
    return mat0, mat1


def regLeaf(dataSet):
    """
    函数说明:生成叶结点
    Parameters:
        dataSet - 数据集合
    Returns:
        目标变量的均值

    """
    return np.mean(dataSet[:, -1])


def regErr(dataSet):
    """
    函数说明:误差估计函数
    Parameters:
        dataSet - 数据集合
    Returns:
        目标变量的总方差

    """
    return np.var(dataSet[:, -1]) * np.shape(dataSet)[0]


def chooseBestSplit(dataSet, leafType=regLeaf, errType=regErr, ops=(1, 4)):
    """
    函数说明:找到数据的最佳二元切分方式函数
    Parameters:
        dataSet - 数据集合
        leafType - 生成叶结点
        regErr - 误差估计函数
        ops - 用户定义的参数构成的元组
    Returns:
        bestIndex - 最佳切分特征
        bestValue - 最佳特征值

    """
    import types
    # tolS允许的误差下降值,tolN切分的最少样本数
    tolS = ops[0];
    tolN = ops[1]
    # 如果当前所有值相等,则退出。(根据set的特性)
    if len(set(dataSet[:, -1].T.tolist()[0])) == 1:
        return None, leafType(dataSet)
    # 统计数据集合的行m和列n
    m, n = np.shape(dataSet)
    # 默认最后一个特征为最佳切分特征,计算其误差估计
    S = errType(dataSet)
    # 分别为最佳误差,最佳特征切分的索引值,最佳特征值
    bestS = float('inf');
    bestIndex = 0;
    bestValue = 0
    # 遍历所有特征列
    for featIndex in range(n - 1):
        # 遍历所有特征值
        for splitVal in set(dataSet[:, featIndex].T.A.tolist()[0]):
            # 根据特征和特征值切分数据集
            mat0, mat1 = binSplitDataSet(dataSet, featIndex, splitVal)
            # 如果数据少于tolN,则退出
            if (np.shape(mat0)[0] < tolN) or (np.shape(mat1)[0] < tolN): continue
            # 计算误差估计
            newS = errType(mat0) + errType(mat1)
            # 如果误差估计更小,则更新特征索引值和特征值
            if newS < bestS:
                bestIndex = featIndex
                bestValue = splitVal
                bestS = newS
    # 如果误差减少不大则退出
    if (S - bestS) < tolS:
        return None, leafType(dataSet)
    # 根据最佳的切分特征和特征值切分数据集合
    mat0, mat1 = binSplitDataSet(dataSet, bestIndex, bestValue)
    # 如果切分出的数据集很小则退出
    if (np.shape(mat0)[0] < tolN) or (np.shape(mat1)[0] < tolN):
        return None, leafType(dataSet)
    # 返回最佳切分特征和特征值
    return bestIndex, bestValue


if __name__ == '__main__':
    myDat = loadDataSet('ex00.txt')
    myMat = np.mat(myDat)
    feat, val = chooseBestSplit(myMat, regLeaf, regErr, (1, 4))
    print(feat)
    print(val)

运行结果如下图所示：

可以看到，切分的最佳特征为第1列特征，最佳切分特征值为0.48813，这个特征值怎么选出来的？就是根据误差估计的大小，我们选择的这个特征值可以使误差最小化。

切分的特征和特征值我们已经选择好了，接下来就是利用选出的这两个变量创建回归树了。

创建方法很简单，我们根据切分的特征和特征值切分出两个数据集，然后将两个数据集分别用于左子树的构建和右子树的构建，直到无法找到切分的特征为止。因此，我们可以使用递归实现这个过程，编写代码如下：

# -*- coding:utf-8 -*-
import numpy as np


def loadDataSet(fileName):
    """
    函数说明:加载数据
    Parameters:
        fileName - 文件名
    Returns:
        dataMat - 数据矩阵

    """
    dataMat = []
    fr = open(fileName)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        fltLine = list(map(float, curLine))  # 转化为float类型
        dataMat.append(fltLine)
    return dataMat


def binSplitDataSet(dataSet, feature, value):
    """
    函数说明:根据特征切分数据集合
    Parameters:
        dataSet - 数据集合
        feature - 带切分的特征
        value - 该特征的值
    Returns:
        mat0 - 切分的数据集合0
        mat1 - 切分的数据集合1

    """
    mat0 = dataSet[np.nonzero(dataSet[:, feature] > value)[0], :]
    mat1 = dataSet[np.nonzero(dataSet[:, feature] <= value)[0], :]
    return mat0, mat1


def regLeaf(dataSet):
    """
    函数说明:生成叶结点
    Parameters:
        dataSet - 数据集合
    Returns:
        目标变量的均值

    """
    return np.mean(dataSet[:, -1])


def regErr(dataSet):
    """
    函数说明:误差估计函数
    Parameters:
        dataSet - 数据集合
    Returns:

    """
    return np.var(dataSet[:, -1]) * np.shape(dataSet)[0]


def chooseBestSplit(dataSet, leafType=regLeaf, errType=regErr, ops=(1, 4)):
    """
    函数说明:找到数据的最佳二元切分方式函数
    Parameters:
        dataSet - 数据集合
        leafType - 生成叶结点
        regErr - 误差估计函数
        ops - 用户定义的参数构成的元组
    Returns:
        bestIndex - 最佳切分特征

    """
    import types
    # tolS允许的误差下降值,tolN切分的最少样本数
    tolS = ops[0];
    tolN = ops[1]
    # 如果当前所有值相等,则退出。(根据set的特性)
    if len(set(dataSet[:, -1].T.tolist()[0])) == 1:
        return None, leafType(dataSet)
    # 统计数据集合的行m和列n
    m, n = np.shape(dataSet)
    # 默认最后一个特征为最佳切分特征,计算其误差估计
    S = errType(dataSet)
    # 分别为最佳误差,最佳特征切分的索引值,最佳特征值
    bestS = float('inf');
    bestIndex = 0;
    bestValue = 0
    # 遍历所有特征列
    for featIndex in range(n - 1):
        # 遍历所有特征值
        for splitVal in set(dataSet[:, featIndex].T.A.tolist()[0]):
            # 根据特征和特征值切分数据集
            mat0, mat1 = binSplitDataSet(dataSet, featIndex, splitVal)
            # 如果数据少于tolN,则退出
            if (np.shape(mat0)[0] < tolN) or (np.shape(mat1)[0] < tolN): continue
            # 计算误差估计
            newS = errType(mat0) + errType(mat1)
            # 如果误差估计更小,则更新特征索引值和特征值
            if newS < bestS:
                bestIndex = featIndex
                bestValue = splitVal
                bestS = newS
    # 如果误差减少不大则退出
    if (S - bestS) < tolS:
        return None, leafType(dataSet)
    # 根据最佳的切分特征和特征值切分数据集合
    mat0, mat1 = binSplitDataSet(dataSet, bestIndex, bestValue)
    # 如果切分出的数据集很小则退出
    if (np.shape(mat0)[0] < tolN) or (np.shape(mat1)[0] < tolN):
        return None, leafType(dataSet)
    # 返回最佳切分特征和特征值
    return bestIndex, bestValue


def createTree(dataSet, leafType=regLeaf, errType=regErr, ops=(1, 4)):
    """
    函数说明:树构建函数
    Parameters:
        dataSet - 数据集合
        leafType - 建立叶结点的函数
        errType - 误差计算函数
        ops - 包含树构建所有其他参数的元组
    Returns:
        retTree - 构建的回归树

    """
    # 选择最佳切分特征和特征值
    feat, val = chooseBestSplit(dataSet, leafType, errType, ops)
    # r如果没有特征,则返回特征值
    if feat == None: return val
    # 回归树
    retTree = {}
    retTree['spInd'] = feat
    retTree['spVal'] = val
    # 分成左数据集和右数据集
    lSet, rSet = binSplitDataSet(dataSet, feat, val)
    # 创建左子树和右子树
    retTree['left'] = createTree(lSet, leafType, errType, ops)
    retTree['right'] = createTree(rSet, leafType, errType, ops)
    return retTree


if __name__ == '__main__':
    myDat = loadDataSet('ex00.txt')
    myMat = np.mat(myDat)
    print(createTree(myMat))

运行结果如下图所示：

从上图可知，这棵树只有两个叶结点。

我们换一个复杂一点的数据集，分段常数数据集。

数据集下载地址：数据集下载

先看下数据：

第一列的数据都是1.0，为了可视化方便，我们将第1列作为x轴数据，第2列作为y轴数据。对数据进行可视化，编写代码如下：

# -*- coding:utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np


def loadDataSet(fileName):
    """
    函数说明:加载数据
    Parameters:
        fileName - 文件名
    Returns:
        dataMat - 数据矩阵

    """
    dataMat = []
    fr = open(fileName)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        fltLine = list(map(float, curLine))  # 转化为float类型
        dataMat.append(fltLine)
    return dataMat


def plotDataSet(filename):
    """
    函数说明:绘制数据集
    Parameters:
        filename - 文件名
    Returns:
        无
    """
    dataMat = loadDataSet(filename)  # 加载数据集
    n = len(dataMat)  # 数据个数
    xcord = [];
    ycord = []  # 样本点
    for i in range(n):
        xcord.append(dataMat[i][1]);
        ycord.append(dataMat[i][2])  # 样本点
    fig = plt.figure()
    ax = fig.add_subplot(111)  # 添加subplot
    ax.scatter(xcord, ycord, s=20, c='blue', alpha=.5)  # 绘制样本点
    plt.title('DataSet')  # 绘制title
    plt.xlabel('X')
    plt.show()


if __name__ == '__main__':
    filename = 'ex0.txt'
    plotDataSet(filename)

运行结果如图下所示：

可以看到，这个数据集是分段的。我们针对此数据集创建回归树。代码同上，运行结果如下所示：

{'spInd': 1, 'spVal': 0.39435, 'left': {'spInd': 1, 'spVal': 0.582002, 'left': {'spInd': 1, 'spVal': 0.797583, 'left': 3.9871632, 'right': 2.9836209534883724}, 'right': 1.980035071428571}, 'right': {'spInd': 1, 'spVal': 0.197834, 'left': 1.0289583666666666, 'right': -0.023838155555555553}}

Process finished with exit code 0

可以看到，该数的结构中包含5个叶结点。

现在为止，已经完成回归树的构建，但是需要某种措施来检查构建过程是否得当。这个技术就是剪枝（tree pruning）技术。

三、树剪枝

一棵树如果结点过多，表明该模型可能对数据进行了“过拟合”。

通过降低树的复杂度来避免过拟合的过程称为剪枝（pruning）。上小节我们也已经提到，设置tolS和tolN就是一种预剪枝操作。另一种形式的剪枝需要使用测试集和训练集，称作后剪枝（postpruning）。本节将分析后剪枝的有效性，但首先来看一下预剪枝的不足之处。

1、预剪枝

预剪枝有一定的局限性，比如我们现在使用一个新的数据集。

数据集下载地址：数据集下载

用上述代码绘制数据集看一下：

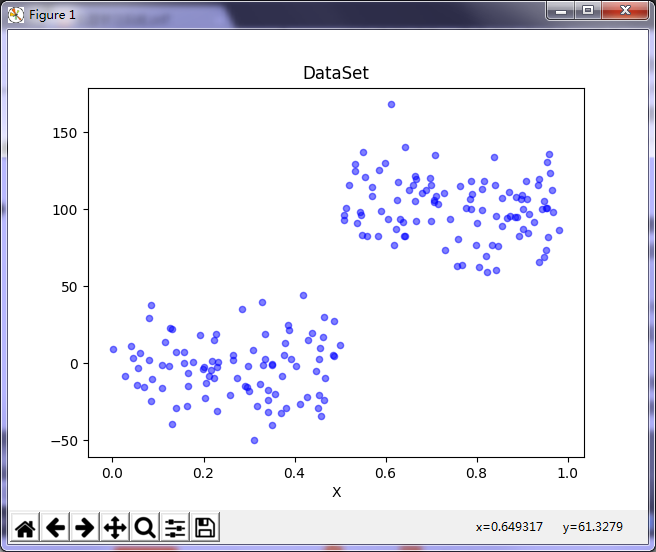
可以看到，对于这个数据集与我们使用的第一个数据集很相似，但是区别在于y的数量级差100倍，数据分布相似，因此构建出的树应该也是只有两个叶结点。但是我们使用默认tolS和tolN参数创建树，你会发现运行结果如下所示：

可以看到，构建出的树有很多叶结点。产生这个现象的原因在于，停止条件tolS对误差的数量级十分敏感。如果在选项中花费时间并对上述误差容忍度取平均值，或许也能得到仅有两个叶结点组成的树：

可以看到，将参数tolS修改为10000后，构建的树就是只有两个叶结点。然而，显然这个值，需要我们经过不断测试得来，显然通过不断修改停止条件来得到合理结果并不是很好的办法。事实上，我们常常甚至不确定到底需要寻找什么样的结果。因为对于一个很多维度的数据集，你也不知道构建的树需要多少个叶结点。

可见，预剪枝有很大的局限性。接下来，我们讨论后剪枝，即利用测试集来对树进行剪枝。由于不需要用户指定参数，后剪枝是一个更理想化的剪枝方法。

2、后剪枝

使用后剪枝方法需要将数据集分成测试集和训练集。首先指定参数，使得构建出的树足够大、足够复杂，便于剪枝。接下来从上而下找到叶结点，用测试集来判断这些叶结点合并是否能降低测试集误差。如果是的话就合并。

为了演示后剪枝，我们使用ex2.txt文件作为训练集，而使用的新数据集ex2test.txt文件作为测试集。

测试集下载地址：数据集下载

现在我们使用ex2.txt训练回归树，然后利用ex2test.txt对回归树进行剪枝。我们需要创建三个函数isTree()、getMean()、prune()。其中isTree()用于测试输入变量是否是一棵树，返回布尔类型的结果。换句话说，该函数用于判断当前处理的结点是否是叶结点。第二个函数getMean()是一个递归函数，它从上往下遍历树直到叶结点为止。如果找到两个叶结点则计算它们的平均值。该函数对树进行塌陷处理（即返回树平均值）。而第三个函数prune()则为后剪枝函数。编写代码如下：

# -*- coding:utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np


def loadDataSet(fileName):
    """
    函数说明:加载数据
    Parameters:
        fileName - 文件名
    Returns:
        dataMat - 数据矩阵
    
    """
    dataMat = []
    fr = open(fileName)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        fltLine = list(map(float, curLine))  # 转化为float类型
        dataMat.append(fltLine)
    return dataMat


def plotDataSet(filename):
    """
    函数说明:绘制数据集
    Parameters:
        filename - 文件名
    Returns:
        无
   
    """
    dataMat = loadDataSet(filename)  # 加载数据集
    n = len(dataMat)  # 数据个数
    xcord = [];
    ycord = []  # 样本点
    for i in range(n):
        xcord.append(dataMat[i][0]);
        ycord.append(dataMat[i][1])  # 样本点
    fig = plt.figure()
    ax = fig.add_subplot(111)  # 添加subplot
    ax.scatter(xcord, ycord, s=20, c='blue', alpha=.5)  # 绘制样本点
    plt.title('DataSet')  # 绘制title
    plt.xlabel('X')
    plt.show()


def binSplitDataSet(dataSet, feature, value):
    """
    函数说明:根据特征切分数据集合
    Parameters:
        dataSet - 数据集合
        feature - 带切分的特征
        value - 该特征的值
    Returns:
        mat0 - 切分的数据集合0
        mat1 - 切分的数据集合1
    
    """
    mat0 = dataSet[np.nonzero(dataSet[:, feature] > value)[0], :]
    mat1 = dataSet[np.nonzero(dataSet[:, feature] <= value)[0], :]
    return mat0, mat1


def regLeaf(dataSet):
    """
    函数说明:生成叶结点
    Parameters:
        dataSet - 数据集合
    Returns:
        目标变量的均值
    
    """
    return np.mean(dataSet[:, -1])


def regErr(dataSet):
    """
    函数说明:误差估计函数
    Parameters:
        dataSet - 数据集合
    Returns:
        目标变量的总方差
    
    """
    return np.var(dataSet[:, -1]) * np.shape(dataSet)[0]


def chooseBestSplit(dataSet, leafType=regLeaf, errType=regErr, ops=(1, 4)):
    """
    函数说明:找到数据的最佳二元切分方式函数
    Parameters:
        dataSet - 数据集合
        leafType - 生成叶结点
        regErr - 误差估计函数
        ops - 用户定义的参数构成的元组
    Returns:
        bestIndex - 最佳切分特征
        bestValue - 最佳特征值
    
    """
    import types
    # tolS允许的误差下降值,tolN切分的最少样本数
    tolS = ops[0];
    tolN = ops[1]
    # 如果当前所有值相等,则退出。(根据set的特性)
    if len(set(dataSet[:, -1].T.tolist()[0])) == 1:
        return None, leafType(dataSet)
    # 统计数据集合的行m和列n
    m, n = np.shape(dataSet)
    # 默认最后一个特征为最佳切分特征,计算其误差估计
    S = errType(dataSet)
    # 分别为最佳误差,最佳特征切分的索引值,最佳特征值
    bestS = float('inf');
    bestIndex = 0;
    bestValue = 0
    # 遍历所有特征列
    for featIndex in range(n - 1):
        # 遍历所有特征值
        for splitVal in set(dataSet[:, featIndex].T.A.tolist()[0]):
            # 根据特征和特征值切分数据集
            mat0, mat1 = binSplitDataSet(dataSet, featIndex, splitVal)
            # 如果数据少于tolN,则退出
            if (np.shape(mat0)[0] < tolN) or (np.shape(mat1)[0] < tolN): continue
            # 计算误差估计
            newS = errType(mat0) + errType(mat1)
            # 如果误差估计更小,则更新特征索引值和特征值
            if newS < bestS:
                bestIndex = featIndex
                bestValue = splitVal
                bestS = newS
    # 如果误差减少不大则退出
    if (S - bestS) < tolS:
        return None, leafType(dataSet)
    # 根据最佳的切分特征和特征值切分数据集合
    mat0, mat1 = binSplitDataSet(dataSet, bestIndex, bestValue)
    # 如果切分出的数据集很小则退出
    if (np.shape(mat0)[0] < tolN) or (np.shape(mat1)[0] < tolN):
        return None, leafType(dataSet)
    # 返回最佳切分特征和特征值
    return bestIndex, bestValue


def createTree(dataSet, leafType=regLeaf, errType=regErr, ops=(1, 4)):
    """
    函数说明:树构建函数
    Parameters:
        dataSet - 数据集合
        leafType - 建立叶结点的函数
        errType - 误差计算函数
        ops - 包含树构建所有其他参数的元组
    Returns:
        retTree - 构建的回归树
    
    """
    # 选择最佳切分特征和特征值
    feat, val = chooseBestSplit(dataSet, leafType, errType, ops)
    # r如果没有特征,则返回特征值
    if feat == None: return val
    # 回归树
    retTree = {}
    retTree['spInd'] = feat
    retTree['spVal'] = val
    # 分成左数据集和右数据集
    lSet, rSet = binSplitDataSet(dataSet, feat, val)
    # 创建左子树和右子树
    retTree['left'] = createTree(lSet, leafType, errType, ops)
    retTree['right'] = createTree(rSet, leafType, errType, ops)
    return retTree


def isTree(obj):
    """
    函数说明:判断测试输入变量是否是一棵树
    Parameters:
        obj - 测试对象
    Returns:
        是否是一棵树
    
    """
    import types
    return (type(obj).__name__ == 'dict')


def getMean(tree):
    """
    函数说明:对树进行塌陷处理(即返回树平均值)
    Parameters:
        tree - 树
    Returns:
        树的平均值
    
    """
    if isTree(tree['right']): tree['right'] = getMean(tree['right'])
    if isTree(tree['left']): tree['left'] = getMean(tree['left'])
    return (tree['left'] + tree['right']) / 2.0


def prune(tree, testData):
    """
    函数说明:后剪枝
    Parameters:
        tree - 树
        test - 测试集
    Returns:
        树的平均值
    
    """
    # 如果测试集为空,则对树进行塌陷处理
    if np.shape(testData)[0] == 0: return getMean(tree)
    # 如果有左子树或者右子树,则切分数据集
    if (isTree(tree['right']) or isTree(tree['left'])):
        lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])
    # 处理左子树(剪枝)
    if isTree(tree['left']): tree['left'] = prune(tree['left'], lSet)
    # 处理右子树(剪枝)
    if isTree(tree['right']): tree['right'] = prune(tree['right'], rSet)
    # 如果当前结点的左右结点为叶结点
    if not isTree(tree['left']) and not isTree(tree['right']):
        lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])
        # 计算没有合并的误差
        errorNoMerge = np.sum(np.power(lSet[:, -1] - tree['left'], 2)) + np.sum(
            np.power(rSet[:, -1] - tree['right'], 2))
        # 计算合并的均值
        treeMean = (tree['left'] + tree['right']) / 2.0
        # 计算合并的误差
        errorMerge = np.sum(np.power(testData[:, -1] - treeMean, 2))
        # 如果合并的误差小于没有合并的误差,则合并
        if errorMerge < errorNoMerge:
            return treeMean
        else:
            return tree
    else:
        return tree


if __name__ == '__main__':
    train_filename = 'ex2.txt'
    train_Data = loadDataSet(train_filename)
    train_Mat = np.mat(train_Data)
    tree = createTree(train_Mat)
    print('剪枝前：')
    print(tree)
    test_filename = 'ex2test.txt'
    test_Data = loadDataSet(test_filename)
    test_Mat = np.mat(test_Data)
    print('剪枝后：')
    print(prune(tree, test_Mat))

运行结果如下如所示：

剪枝前：
{'spInd': 0, 'spVal': 0.499171, 'left': {'spInd': 0, 'spVal': 0.729397, 'left': {'spInd': 0, 'spVal': 0.952833, 'left': {'spInd': 0, 'spVal': 0.958512, 'left': 105.24862350000001, 'right': 112.42895575000001}, 'right': {'spInd': 0, 'spVal': 0.759504, 'left': {'spInd': 0, 'spVal': 0.790312, 'left': {'spInd': 0, 'spVal': 0.833026, 'left': {'spInd': 0, 'spVal': 0.944221, 'left': 87.3103875, 'right': {'spInd': 0, 'spVal': 0.85497, 'left': {'spInd': 0, 'spVal': 0.910975, 'left': 96.452867, 'right': {'spInd': 0, 'spVal': 0.892999, 'left': 104.825409, 'right': {'spInd': 0, 'spVal': 0.872883, 'left': 95.181793, 'right': 102.25234449999999}}}, 'right': 95.27584316666666}}, 'right': {'spInd': 0, 'spVal': 0.811602, 'left': 81.110152, 'right': 88.78449880000001}}, 'right': 102.35780185714285}, 'right': 78.08564325}}, 'right': {'spInd': 0, 'spVal': 0.640515, 'left': {'spInd': 0, 'spVal': 0.666452, 'left': {'spInd': 0, 'spVal': 0.706961, 'left': 114.554706, 'right': {'spInd': 0, 'spVal': 0.698472, 'left': 104.82495374999999, 'right': 108.92921799999999}}, 'right': 114.1516242857143}, 'right': {'spInd': 0, 'spVal': 0.613004, 'left': 93.67344971428572, 'right': {'spInd': 0, 'spVal': 0.582311, 'left': 123.2101316, 'right': {'spInd': 0, 'spVal': 0.553797, 'left': 97.20018024999999, 'right': {'spInd': 0, 'spVal': 0.51915, 'left': {'spInd': 0, 'spVal': 0.543843, 'left': 109.38961049999999, 'right': 110.979946}, 'right': 101.73699325000001}}}}}}, 'right': {'spInd': 0, 'spVal': 0.457563, 'left': {'spInd': 0, 'spVal': 0.467383, 'left': 12.50675925, 'right': 3.4331330000000007}, 'right': {'spInd': 0, 'spVal': 0.126833, 'left': {'spInd': 0, 'spVal': 0.373501, 'left': {'spInd': 0, 'spVal': 0.437652, 'left': -12.558604833333334, 'right': {'spInd': 0, 'spVal': 0.412516, 'left': 14.38417875, 'right': {'spInd': 0, 'spVal': 0.385021, 'left': -0.8923554999999995, 'right': 3.6584772500000016}}}, 'right': {'spInd': 0, 'spVal': 0.335182, 'left': {'spInd': 0, 'spVal': 0.350725, 'left': -15.08511175, 'right': -22.693879600000002}, 'right': {'spInd': 0, 'spVal': 0.324274, 'left': 15.05929075, 'right': {'spInd': 0, 'spVal': 0.297107, 'left': -19.9941552, 'right': {'spInd': 0, 'spVal': 0.166765, 'left': {'spInd': 0, 'spVal': 0.202161, 'left': {'spInd': 0, 'spVal': 0.217214, 'left': {'spInd': 0, 'spVal': 0.228473, 'left': {'spInd': 0, 'spVal': 0.25807, 'left': 0.40377471428571476, 'right': -13.070501}, 'right': 6.770429}, 'right': -11.822278500000001}, 'right': 3.4496025}, 'right': {'spInd': 0, 'spVal': 0.156067, 'left': -12.1079725, 'right': -6.247900000000001}}}}}}, 'right': {'spInd': 0, 'spVal': 0.084661, 'left': 6.509843285714284, 'right': {'spInd': 0, 'spVal': 0.044737, 'left': -2.544392714285715, 'right': 4.091626}}}}}
剪枝后：
{'spInd': 0, 'spVal': 0.499171, 'left': {'spInd': 0, 'spVal': 0.729397, 'left': {'spInd': 0, 'spVal': 0.952833, 'left': {'spInd': 0, 'spVal': 0.958512, 'left': 105.24862350000001, 'right': 112.42895575000001}, 'right': {'spInd': 0, 'spVal': 0.759504, 'left': {'spInd': 0, 'spVal': 0.790312, 'left': {'spInd': 0, 'spVal': 0.833026, 'left': {'spInd': 0, 'spVal': 0.944221, 'left': 87.3103875, 'right': {'spInd': 0, 'spVal': 0.85497, 'left': {'spInd': 0, 'spVal': 0.910975, 'left': 96.452867, 'right': {'spInd': 0, 'spVal': 0.892999, 'left': 104.825409, 'right': {'spInd': 0, 'spVal': 0.872883, 'left': 95.181793, 'right': 102.25234449999999}}}, 'right': 95.27584316666666}}, 'right': {'spInd': 0, 'spVal': 0.811602, 'left': 81.110152, 'right': 88.78449880000001}}, 'right': 102.35780185714285}, 'right': 78.08564325}}, 'right': {'spInd': 0, 'spVal': 0.640515, 'left': {'spInd': 0, 'spVal': 0.666452, 'left': {'spInd': 0, 'spVal': 0.706961, 'left': 114.554706, 'right': 106.87708587499999}, 'right': 114.1516242857143}, 'right': {'spInd': 0, 'spVal': 0.613004, 'left': 93.67344971428572, 'right': {'spInd': 0, 'spVal': 0.582311, 'left': 123.2101316, 'right': 101.580533}}}}, 'right': {'spInd': 0, 'spVal': 0.457563, 'left': 7.969946125, 'right': {'spInd': 0, 'spVal': 0.126833, 'left': {'spInd': 0, 'spVal': 0.373501, 'left': {'spInd': 0, 'spVal': 0.437652, 'left': -12.558604833333334, 'right': {'spInd': 0, 'spVal': 0.412516, 'left': 14.38417875, 'right': 1.383060875000001}}, 'right': {'spInd': 0, 'spVal': 0.335182, 'left': {'spInd': 0, 'spVal': 0.350725, 'left': -15.08511175, 'right': -22.693879600000002}, 'right': {'spInd': 0, 'spVal': 0.324274, 'left': 15.05929075, 'right': {'spInd': 0, 'spVal': 0.297107, 'left': -19.9941552, 'right': {'spInd': 0, 'spVal': 0.166765, 'left': {'spInd': 0, 'spVal': 0.202161, 'left': -5.801872785714286, 'right': 3.4496025}, 'right': {'spInd': 0, 'spVal': 0.156067, 'left': -12.1079725, 'right': -6.247900000000001}}}}}}, 'right': {'spInd': 0, 'spVal': 0.084661, 'left': 6.509843285714284, 'right': {'spInd': 0, 'spVal': 0.044737, 'left': -2.544392714285715, 'right': 4.091626}}}}}

Process finished with exit code 0

可以看到，树的大量结点已经被剪枝掉了，但没有像预期的那样剪枝成两部分，这说明后剪枝可能不如预剪枝有效。一般地，为了寻求最佳模型可以同时使用两种剪枝技术。

现在，可能你会问了，这叶结点只是简单的数值。这也没有拟合数据啊？回归树到底啥样啊？别急，下篇文章继续讲解。

四、总结

  • CART算法可以用于构建二元树并处理离散型或连续型数据的切分。若使用不同的误差准则，就可以通过CART算法构建模型树和回归树。

  • 一颗过拟合的树常常十分复杂，剪枝技术的出现就是为了解决这个问题。两种剪枝方法分别是预剪枝和后剪枝，预剪枝更有效但需要用户定义一些参数。

  • 下篇文章将继续讲解回归树。

参考资料：

  • [1] 机器学习实战第八章内容

  • [2] 统计学习方法第五章内容

  • https://cuijiahua.com/blog/2017/12/ml_13_regtree_1.html

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/151779.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

成功上岸字节全靠这份Redis技术笔记，深入浅出值得一看

成功上岸字节全靠这份Redis技术笔记，深入浅出值得一看

前言 正如标题所说&#xff0c;我现在已经如愿以偿地进了字节&#xff01;之前自己一直待在一个不大不小的外包公司&#xff0c;每天做着重复的层删改查工作。直到22年年底&#xff0c;自己通过朋友的介绍拿到了字节的面试机会&#xff0c;自己在家复习了3个月&#xff0c;成功…
阅读更多...
decltype类型指示符

decltype类型指示符

decltype类型指示符一、什么是decltype类型指示符二、typeid运算符三、使用decltype指示符四、decltype和引用五、decltype(auto)六、本章代码汇总一、什么是decltype类型指示符 有时会遇到这种情况&#xff1a;希望从表达式的类型推断出要定义的变量的类型&#xff0c;但是不…
阅读更多...
超实用的实用Shell脚本

超实用的实用Shell脚本

一、Dos 攻击防范&#xff08;自动屏蔽攻击 IP&#xff09; 代码&#xff1a; #!/bin/bash DATE$(date %d/%b/%Y:%H:%M) LOG_FILE/usr/local/nginx/logs/demo2.access.log ABNORMAL_IP$(tail -n5000 $LOG_FILE |grep $DATE |awk {a[$1]}END{for(i in a)if(a[i]>10)print…
阅读更多...
Spring 学习笔记2

Spring 学习笔记2

1.spring设置JDBC链接池 classpath:jdbc.properties是有多个连接池时的写法&#xff0c;一般都用这种 还有就是配置文件里不要直接使用username&#xff0c;会被覆盖 使用${}来从文件里读取属性 <beans xmlns"http://www.springframework.org/schema/beans"xmlns…
阅读更多...
bitmap原理+性能优化实践

bitmap原理+性能优化实践

目录 背景 总体结构 从RoaringBitmp说起 3.1arraycontainer 1.3.2 bitmapcontainer 1.3.3 runcontainer 上源码 Roaring64NavigableMap RoaringBitmap RoaringArray 三种Container ArrayContainer BitmapContainer RunContainer 工作应用 需求 分析 能否多线…
阅读更多...
ArcGIS基础实验操作100例--实验75气体扩散空间分析

ArcGIS基础实验操作100例--实验75气体扩散空间分析

本实验专栏参考自汤国安教授《地理信息系统基础实验操作100例》一书 实验平台&#xff1a;ArcGIS 10.6 实验数据&#xff1a;请访问实验1&#xff08;传送门&#xff09; 高级编辑篇--实验75 气体扩散空间分析 目录 一、实验背景 二、实验数据 三、实验步骤 &#xff08;1&…
阅读更多...
MySQL常用基础 - 小白必看（二）

MySQL常用基础 - 小白必看（二）

MySQL数据库基本操作 一、DDL 概念&#xff1a;是一个数据定义语言 该语言部分包括&#xff1a; 1、对数据库的常用操作 创建数据库&#xff1a; 1、create database 数据库名 (直接删除) 2、create database if not exists 数据库名 &#xff08;判断数据库是否存在&…
阅读更多...
视频的水印怎样去掉？这些去水印的方法值得你试试看

视频的水印怎样去掉？这些去水印的方法值得你试试看

喜欢视频剪辑的你会不会经常遇到这种情况&#xff1a;每次上网查找的视频素材&#xff0c;保存下来后总是带有一些水印&#xff0c;这些水印不仅不够美观&#xff0c;而且还会遮挡住视频的一些部分&#xff0c;实在是烦人。如果你遇到这种情况&#xff0c;会很想知道“给视频无…
阅读更多...
86、【栈与队列】leetcode ——39. 滑动窗口最大值：单调队列+滑动窗口（C++版本）

86、【栈与队列】leetcode ——39. 滑动窗口最大值：单调队列+滑动窗口（C++版本）

题目描述 239. 滑动窗口最大值 一、单调队列滑动窗口方法 本题的特点是维护一个窗口&#xff0c;在窗口不断向前移动时&#xff0c;获取其中的最大值。由于窗口在向前移动过程中&#xff0c;元素存在着进入和出去的连续顺序&#xff0c;与FIFO的特点类似。 故可考虑用队列实…
阅读更多...
【数据结构】初识数据结构，十分钟带你玩转算法复杂度

【数据结构】初识数据结构，十分钟带你玩转算法复杂度

目录 &#x1f34a;前言&#x1f34a;&#xff1a; &#x1f95d;一、初识数据结构&#x1f95d;&#xff1a; 1.数据结构&#xff1a; 2.算法&#xff1a; &#x1f353;二、算法效率&#x1f353;&#xff1a; &#x1f348;三、算法复杂度&#x1f348;&#xff1a; 1.时…
阅读更多...
4-1文件管理-文件系统基础

4-1文件管理-文件系统基础

文章目录一.文件的基本概念二.文件的逻辑结构&#xff08;一&#xff09;无结构文件/流式文件&#xff08;二&#xff09;有结构文件1.顺序文件2.索引文件3.索引顺序文件4.直接文件/散列文件三.文件目录四.文件的物理结构/文件分配方式1.连续分配2.链接分配3.索引分配五.文件存…
阅读更多...
数据结构与算法基础（王卓）（8）附：关于new的使用方法详解

数据结构与算法基础（王卓）（8）附：关于new的使用方法详解

part 1&#xff1a; C中new的用法&#xff08;不过就是&#xff09;如下&#xff08;几种用法&#xff09;&#xff1a; 1&#xff1a; new<数据类型> 分配&#xff1a; 指定类型的&#xff0c;大小为1的&#xff0c;内存空间&#xff1b; int *i new int;//注意&am…
阅读更多...
13_3、Java的IO流之节点流的使用

13_3、Java的IO流之节点流的使用

一、FileReader和FileWriter的使用1、数据读入操作说明&#xff1a;①read():返回读入的第一个字符&#xff0c;当读到文档末尾&#xff0c;返回-1②异常的处理&#xff1a;为了保证流资源一定会执行关闭操作&#xff0c;要对异常进行try-catch-finally处理③对于读入操作&…
阅读更多...
【PWA学习】1. 初识 PWA

【PWA学习】1. 初识 PWA

什么是PWA PWA(Progressive Web Apps&#xff0c;渐进式 Web 应用)运用现代的 Web API 以及传统的渐进式增强策略来创建跨平台 Web 应用程序。这些应用无处不在、功能丰富&#xff0c;使其具有与原生应用相同的用户体验优势 我们需要理解的是&#xff0c;PWA 不是某一项技术&am…
阅读更多...
MAC(m1)-VMWare Fusion CentOS8设置静态IP、SSH连接

MAC(m1)-VMWare Fusion CentOS8设置静态IP、SSH连接

在使用虚拟机的时候&#xff0c;默认情况下使用的DHCP协议&#xff08;根据网段自动分配ip&#xff09;分配的动态IP地址&#xff0c; 使得每次打开虚拟机后当前的IP地址都会发生变化&#xff0c;这样不方便管理。为了能够给当前虚拟机设置 一个静态IP地址&#xff0c;方便后…
阅读更多...
Linux的开发工具——软件包管理器 yum

Linux的开发工具——软件包管理器 yum

目录 1 查看 2 安装 3 卸载 4 常用软件 5 扩展细节 5.1 yum源 什么是软件包 在Linux下安装软件, 一个通常的办法是下载到程序的源代码, 并进行编译, 得到可执行程序. 但是这样太麻烦了, 于是有些人把一些常用的软件提前编译好, 做成软件包(可以理解成window…
阅读更多...
【自学Python】Python标识符和保留字

【自学Python】Python标识符和保留字

Python标识符 Python标识符教程 Python 对各种 变量、方法、函数等命名时使用的字符序列称为标识符。 也可以说凡是自己可以起名字的地方都叫标识符&#xff0c;简单地理解&#xff0c;标识符就是一个名字&#xff0c;它的主要作用就是作为变量、函数、类、模块以及其他对象…
阅读更多...
柱承重式钢模块建筑结构体系适用高度研究

柱承重式钢模块建筑结构体系适用高度研究

作者&#xff1a;陈志华 冯云鹏 刘佳迪 刘洋 钟旭 模块建筑网 导语 摘要&#xff1a;模块建筑作为一种新兴的建筑体系&#xff0c;具有较高的预制化和装配化程度&#xff0c;符合建筑工业化以及绿色建筑的发展要求&#xff0c;但国内的模块建筑大多只应用于低多层&#xff0c;…
阅读更多...
[付源码+数据集]Github星标上万，23 个机器学习项目汇总

[付源码+数据集]Github星标上万，23 个机器学习项目汇总

在本文中分享了涵盖面向初学者&#xff0c;中级专家和专家的23种机器学习项目创意&#xff0c;以获取有关该增长技术的真实经验。这些机器学习项目构想将帮助你了解在职业生涯中取得成功、和当下就业所需的所有实践。 通过项目学习是你短期内能做的最好投资&#xff0c;这些项…
阅读更多...
.NET 6结合SkiaSharp实现拼接验证码功能

.NET 6结合SkiaSharp实现拼接验证码功能

从最初的滑动验证码&#xff0c;到实现旋转验证码&#xff01;不光实践了SkiaSharp的使用&#xff0c;也学到了很多东西。在网上看到一个拼接验证码功能&#xff0c;手痒了起来&#xff0c;结合前面实现的两种验证码&#xff0c;我们来学习一下如何实现拼接验证码功能&#xff…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023