题目描述

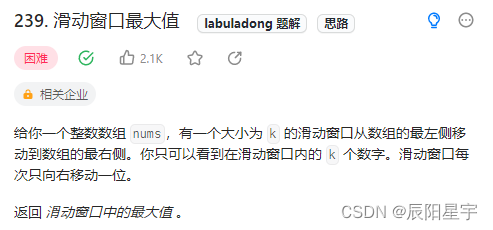
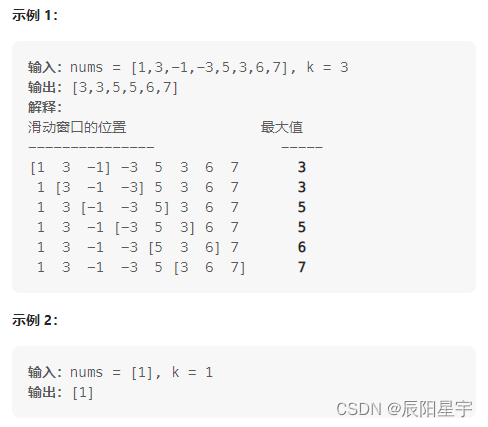
在这里插入图片描述

239. 滑动窗口最大值

一、单调队列+滑动窗口方法

本题的特点是维护一个窗口，在窗口不断向前移动时，获取其中的最大值。由于窗口在向前移动过程中，元素存在着进入和出去的连续顺序，与FIFO的特点类似。

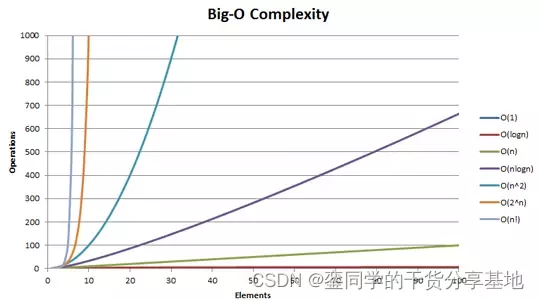
故可考虑用队列实现。而优先队列（按某种优先级顺序排列）正好满足我们的需求，但每次维护顺序时，需要进行堆排序，时间复杂度会是 $O (n l o g n)$ 。

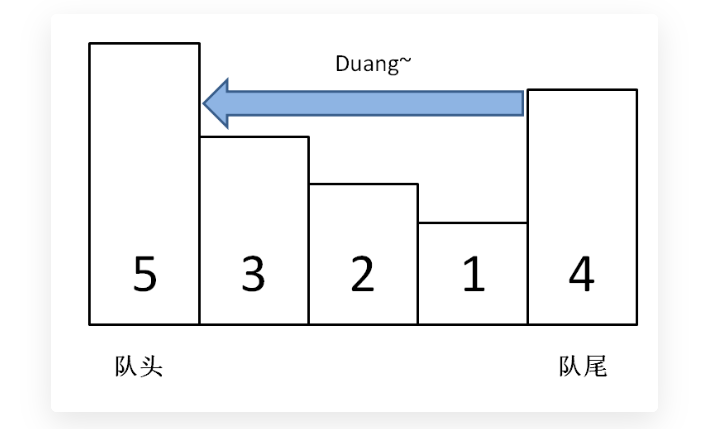
但本题我们实际上只需要维护最近中的最大值元素而已，并不需要对所有添加过的元素都进行维护，因此我们可使用单调队列（队列内元素单调不减或单调不增），保证队头元素为最大值，队内元素按单调不增排列。每次从队尾加入元素，当已存入的队尾元素比待加入元素小时，弹出旧元素，直至队尾当前指向元素大于或等于待加入元素时，将其加入队尾，从而实现队内单调不减。可保证维护对顺序的时间复杂度为 $O (n)$ 。

在移动窗口的过程中，当队头元素与移除元素相同时，则弹出。不同时，则不弹出。然后将进入窗口的元素加入到队内，每次都将队头中的最大值加入到结果集中。

class Solution {
public:
    // 构建一个单调队列（队列中的数值由大到小，单调不减）
    class MyDeque {
    public:
        deque<int> que;
        // 从队头弹出与目标相等的数
        void pop(int value) {
        	// 若移出窗口元素不为最大值，则在此之前已被弹出。若为最大值，则此时会弹出。
            if(!que.empty() && que.front() == value) {
                que.pop_front();
            }
        }
        // 压入数并保证队列内的数由大到小，单调不减排列
        void push(int value) {
            // 当最后一个数小于待入队的数时，将队尾处的元素弹出，直至队尾指向元素大于等于待入队元素
            while(!que.empty() && que.back() < value) {
                que.pop_back();
            }
            // 当最后一个数大于或等于待入队元素时，存入队尾
            que.push_back(value);
        }
        // 获取队首元素（最大值）
        int front() {
            return que.front();
        }
    };
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        MyDeque que;
        vector<int> res;
        // 先将前k个数入队，列出最大值
        for(int i = 0; i < k; i++) {
            que.push(nums[i]);
        }
        res.push_back(que.front());
        // 之后每次都对比队首弹出一个元素，再入队一个元素，将最大值再加入res中
        for(int i = k; i < nums.size(); i++) {
            // 弹出移出窗口元素
            que.pop(nums[i - k]);
            // 加入进入窗口元素
            que.push(nums[i]);
            // 获取窗口内的最大值，加入进去
            res.push_back(que.front());
        }
        return res;
    }
};