【数据结构】哈希表（哈希函数+负载因子+解决冲突方法）

news2024/9/25 17:12:52

文章目录

- 五、哈希表
- - 1.概念
  - 2.哈希函数
  - - 1.设计哈希函数：
    - 2.常见的哈希函数
    - - 1.直接定址法（常用）：
      - 2.除留余数法（常用）
    - 3.负载因子
    - 4.解决冲突
    - - 1.闭散列法（开放地址法）
      - 1.线性探测法：冲突的时候，放到下一个空的位置
        2.二次探测：
      - 2.开散列法（哈希桶）
    - 5.HashBunk（哈希桶的实现）

五、哈希表

1.概念

查找的时间复杂度：二分查找为 o（N）,搜索树为o(log₂N) 哈希表为 o(1)
通过关键字Key来快速找到对应的值，不比较，直接找到。
通过一个函数将关键字和存储位置直接建立一一对应的关系，从而避免了不断的比较查找

这种映射的方法叫哈希（散列）方法，函数叫哈希函数，构造的结构叫哈希表（HashTable）

2.哈希函数

hash(key) = key % capacity

capacity是存储空间的大小

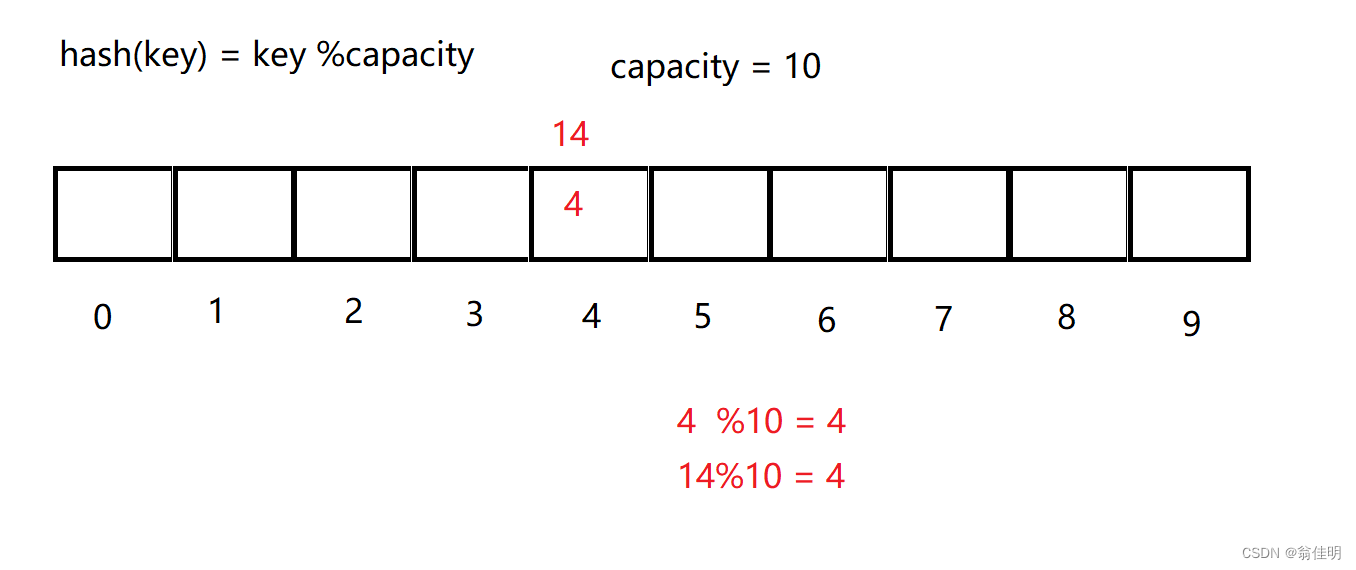
在这里插入图片描述

哈希冲突：当两个不同的值，经过哈希函数，得到相同的地址时，发生哈希碰撞
发生冲突的原因：1.存储的容量小于要存储的数量。2.哈希函数的设计不合理
哈希冲突无法解决，只能尽量降低冲突率

1.设计哈希函数：

1.要足够简单

2.计算的地址在空间中均匀分布

3.有m个地址，值域为0到m-1

2.常见的哈希函数

1.直接定址法（常用）：

Hash（Key）= A*Key + B 关键字的线性函数

优点：简单、均匀
缺点：需要事先知道关键字的分布情况
场景：查找比较小且连续的数

2.除留余数法（常用）

Hash(key) = key% p(p<=m)

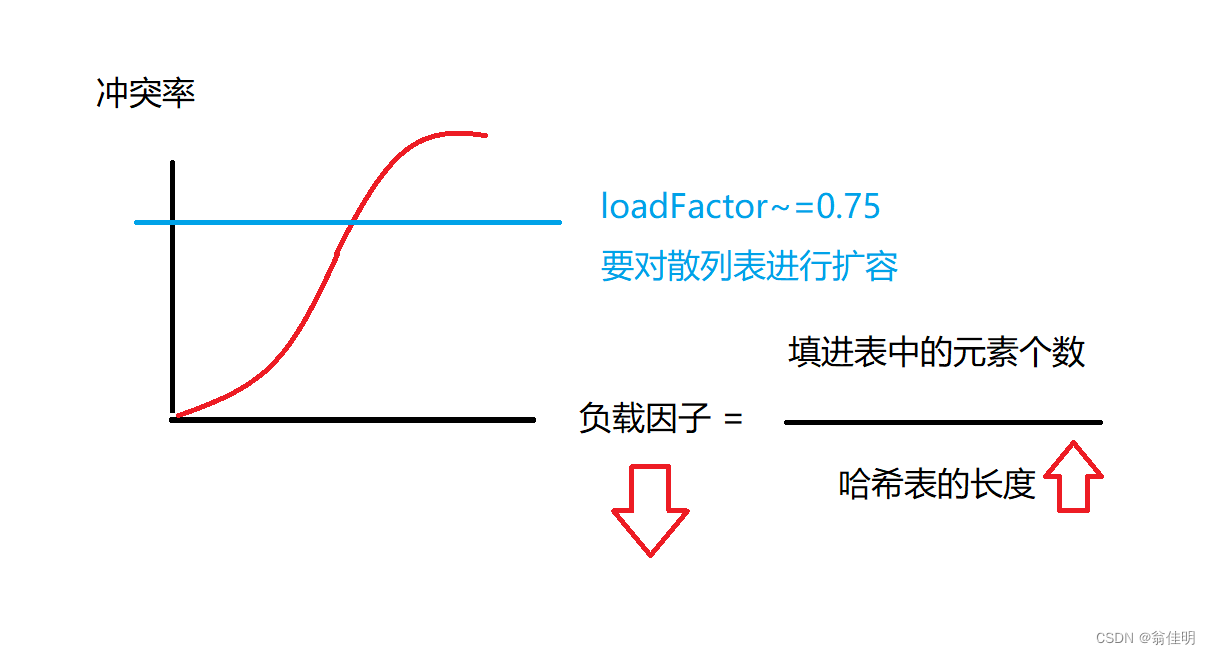
3.负载因子

负载因子 a = 填进表中的元素个数 / 哈希表的长度
在这里插入图片描述

4.解决冲突

1.闭散列法（开放地址法）

1.线性探测法：冲突的时候，放到下一个空的位置

缺点：将冲突的元素放在了一起

在这里插入图片描述

2.二次探测：

在这里插入图片描述

缺点：空间利用率低
解决了线性探测聚到一起的问题
超过0.5要扩容

2.开散列法（哈希桶）

也叫链地址法、开链法
数组+链表：数组的每个元素就是链表的头结点
数组+链表+红黑树（当数组长度>=64 && 链表长度 >=8 以后，把链表变成红黑树，小于又变回去【树化、解树化】）

在这里插入图片描述

JDK7以前：用头插法存进数组中的链表

JDK8以后：采用尾插法

5.HashBunk（哈希桶的实现）

哈希桶的结构

public class HashBunk {
    static class Node {
        int key;
        int val;
        Node next;

        public Node(int key, int val) {
            this.key = key;
            this.val = val;
        }
    }

    public Node[] array;
    public int usedSize;
    public static final float DEFAULT_LOAD_FACTOR = 0.75f;//负载因子

    public HashBunk() {
        array = new Node[10];
    }
}

哈希桶的插入：采用尾插法实现

 /**
     * 哈希桶的插入
     *
     * @param key
     * @param val
     */
    public void put(int key, int val) {

        int index = key % array.length;
        //找到要插入的链表所在数组的下标标

        Node cur = array[index];
        //遍历index处的链表，看是否存在Key,
        // 存在，跟新val
        //不存在，进行尾插法
        while (cur != null) {
            if (cur.key == key) {
                cur.val = val;//key存在，更新val
                return;
            }
            cur = cur.next;
        }
        if (array[index]==null){
            Node node = new Node(key, val);
            array[index]=node;
            usedSize++;
        }else {
            cur = array[index];
            while (cur.next!=null){
                cur = cur.next;
            }
            //进行尾插法
            Node node = new Node(key, val);
            cur.next = node;
            node.next = null;
            usedSize++;

        }
        //计算当前负载因子
        if (doLoadFactor() > DEFAULT_LOAD_FACTOR) {
            //进行扩容，不光要改变数组的大小，还要重新确定链表的首地址
            //因为之前的首地址是按照之前的容量大小计算出来的。
            resize();
        }
    }

数组大小的扩容，同时要重新确定链表中每个结点的位置

    private void resize() {
        Node[] newArray = new Node[2 * array.length];
        for (int i = 0; i < array.length; i++) {
            //遍历原来的数组
            Node cur = array[i];
            //得到原来数组的首结点
            while (cur != null) {
                //遍历链表
                int newIndex = cur.key % newArray.length;
                Node tmp = cur.next;
                Node node = cur;
                node.next = null;
                if (newArray[newIndex] == null) {
                    newArray[newIndex] = node;
                } else {
                    Node lastNode = getLastNode(newArray[newIndex]);
                    lastNode.next = node;
                }
                cur = tmp;
            }
        }
        array = newArray;
    }

    private Node getLastNode(Node cur) {
        while (cur.next != null) {
            cur = cur.next;
        }
        return cur;
    }

    private float doLoadFactor() {
        return usedSize * 1.0f / array.length;

    }

    public int get(int key){
        int index = key%array.length;
        Node cur = array[index];
        while (cur!=null){
            if (cur.key==key){
                return cur.val;
            }
            cur = cur.next;
        }
        return -1;
    }