数据结构,指的是数据元素之间的相互关系,尤其是数据的逻辑结构。选择数据结构的主要依据是数据的逻辑结构[6]。 因此， 本章将主要描述三种数据的逻辑结构。这三种数据包括：二维几何数据、三维几何数据和拓扑数据。

1 数据结构模块的整体框架

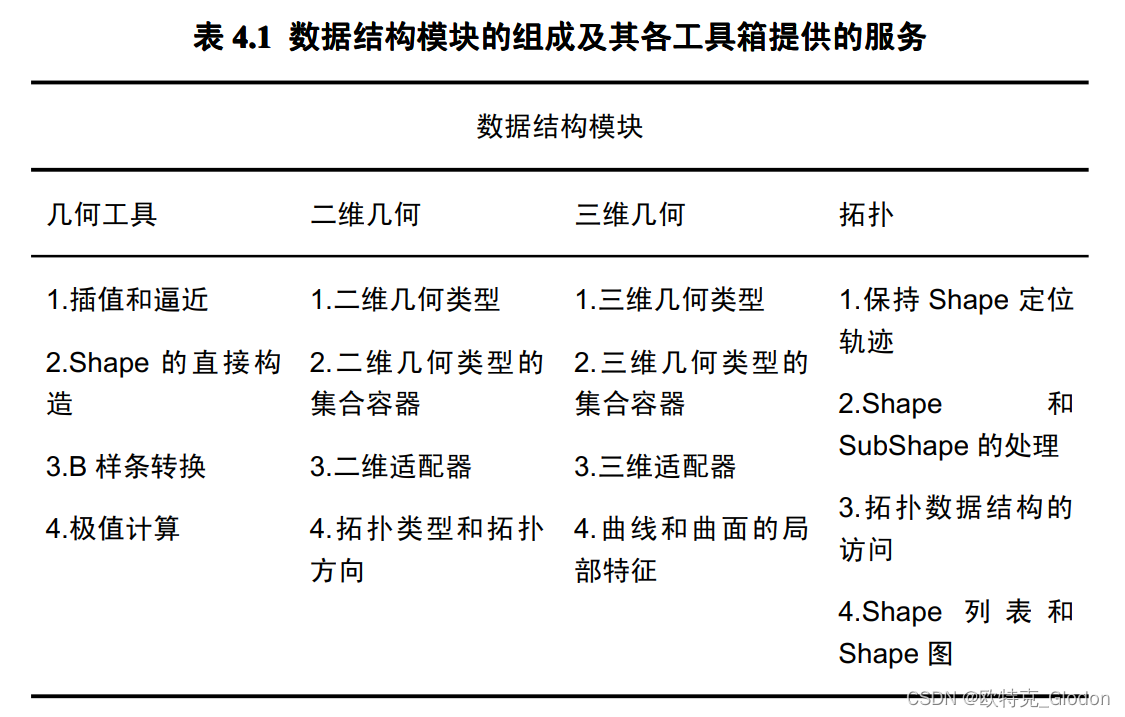
  OCC 的第二个模块是建模数据，也称数据结构。它主要为二维和三维几何模型提供数据结构。数据结构模块由四个工具箱组成：几何工具、二维几何、 三维几何和拓扑。各个工具箱提供的服务如表 4.1 所示。

2 二维几何数据结构

2.1 概述

  二维几何数据结构定义了二维空间上几何对象的数据结构， 主要由 Geom2d包提供。Geom2d 包提供了比 gp 包更大范围的对象。这些对象是非持久的，并且是通过引用而不是通过数值处理的。 复制一个实例， 只是将句柄拷贝而已， 对象没有被拷贝。 因此， 对一个实例（对象） 的改变， 将在所有引用它的地方发生改变。如果需要的对象不是单一的， 而是一系列的， 那么TColGeom2d 包（用来处理这类对象的集合容器） 将提供必要的功能。 特别地， 该包为通用类中那些标准的和经常使用的实例化提供几何对象。

  TColGeom2d 包为来自 Geom2d 包的曲线提供一维数组、 二维数组和序列的实现。所有这些对象能以两种不同的方式处理：句柄处理和数值处理。

2.2 TopAbs 包

  TopAbs 包提供通用枚举类， 用来描述拓扑学基本概念和处理枚举类的方法，不包含具体类。该包已经从拓扑包中分离出来了，因为对于所有拓扑工具而言，它的概念已经足够通用了， 可以通过保留独立的模型资源， 避免枚举类的重复定义。 TopAbs 定义了三个概念： 拓扑类型（由 TopAbs_ShapeEnum 类描述）、 拓扑方向(由 TopAbs_Orientation 类描述)和拓扑状态(由 TopAbs_State 类描述)。

2.2.1 拓扑类型

  TopAbs_ShapeEnum 枚举类列出了不同的拓扑类型。 一个拓扑模型可以看作一个由多个彼此相邻的对象组成的图表。 当在二维或三维空间上建立模型的一部分的时候，该部分的类型必须是 ShapeEnum 枚举类列出的类型之一。对于任何一个模型，里面可以找到的所有对象， TopAbs 包都列出了。 Top- Abs 包不能再扩展，但是可以用到它的一部分，例如，实心体的概念在二维中是没有意义的。

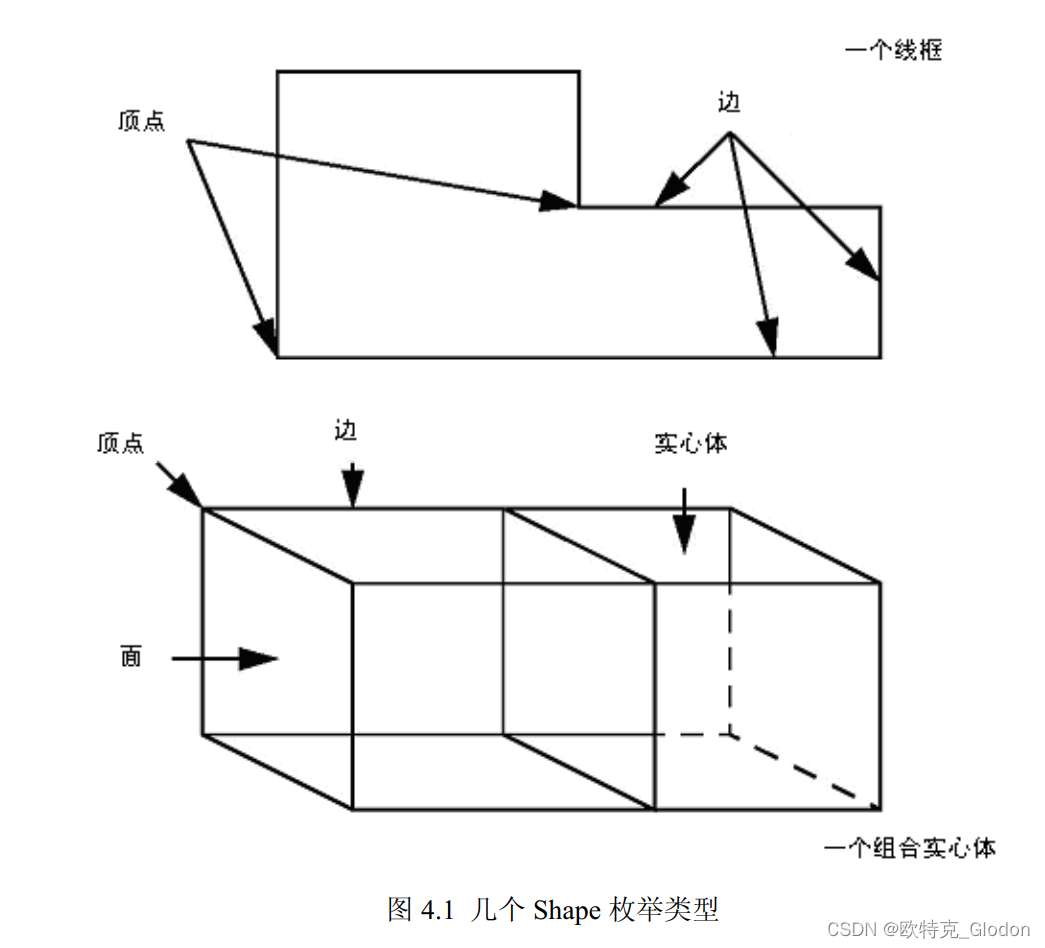
  表 4.2 给出 ShapeEnum 枚举类的各元素及其意义。表 4.2 中出现的枚举类术语是从复杂到简单依次排列的，因为在描述对象时， 可以说对象包含更简单的对象。 例如， 一个面引用了它的线框、 边和顶点。为了进一步理解 Shape 枚举类型，给出一个示意图（图 4.1），图中表示了部分Shape 枚举类型。

2.2.2 拓扑方向

  拓扑方向的概念由 TopAbs_Orientation 枚举类描述。 在许多建模器里都用到了方向；拓扑方向就是这种方向感的通用概念。当一个 Shape 限制了一个几何域时， 就说这个 Shape 具有拓扑方向。 拓扑方向的概念与边界的概念紧密联系。 需要用到拓扑方向的三种 Shape 有： 由顶点限制的曲线、 由边限制的曲面和由面限制的空间。

  无论哪种 Shape（作为维数更高的空间几何域的边界） 都定义了两个局部段，其中一个被指定为默认段。

  对于一条由顶点限制的曲线， 默认段就是一系列点（这些点的参数比顶点的大）。也就是说，沿着曲线方向，除去顶点，其它所有点就是该曲线的默认段。对于一个由边限制的曲面，它的默认段位于边的左边（沿着边的自然方向看， 即沿着逆时针方向看）。确切地说，默认段由曲面法向量和曲线切向量指出。对于一个由面限制的空间，它的默认段位于与曲面法向相反一边。

  基于这个默认段， 拓扑方向允许对保留段（称为 Shape 的内部或 Shape 的材质）进行定义。定义 Shape 的内部有四种拓扑方向，如表 4.3 所示。

  拓扑方向是一个非常通用的概念，只要有段或边界出现的地方就可以用到它。 例如， 当需要描述一条边与一个轮廓的交叉时， 不但可描述出交叉段的定点，而且可以描述出这条边是如何穿越该轮廓的——将边当成轮廓的一个边界， 如图4.2 所示。

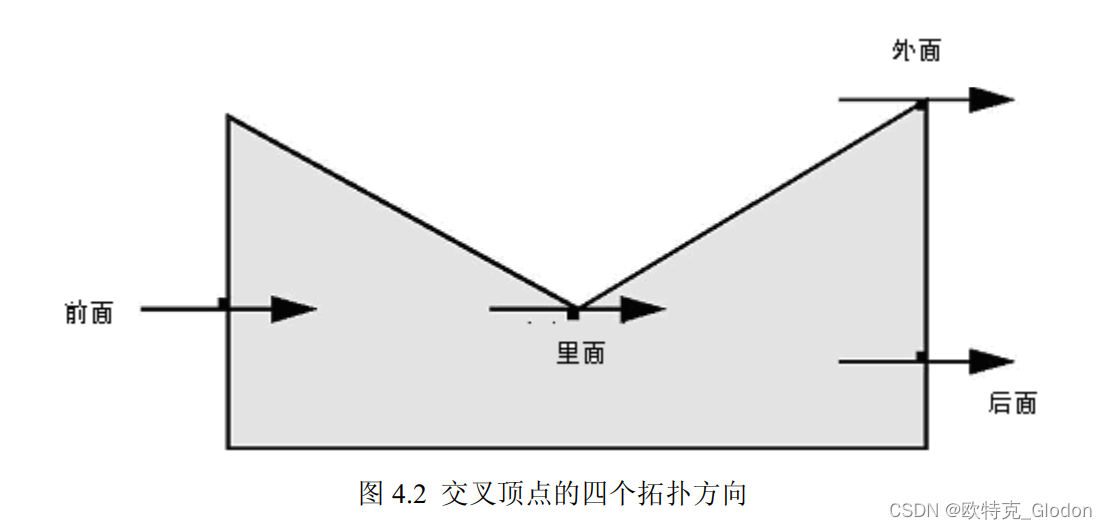
表 4.4 给出了这四个拓扑方向的文字描述。

与 Orientation 枚举类对应， TopAbs 包定义了四种方法，如表 4.5 所示。

2.2.3 拓扑状态

  TopAbs_State 枚举类描述了段上一个或一组顶点的位置。 有四种位置， 如表4.6 所示。

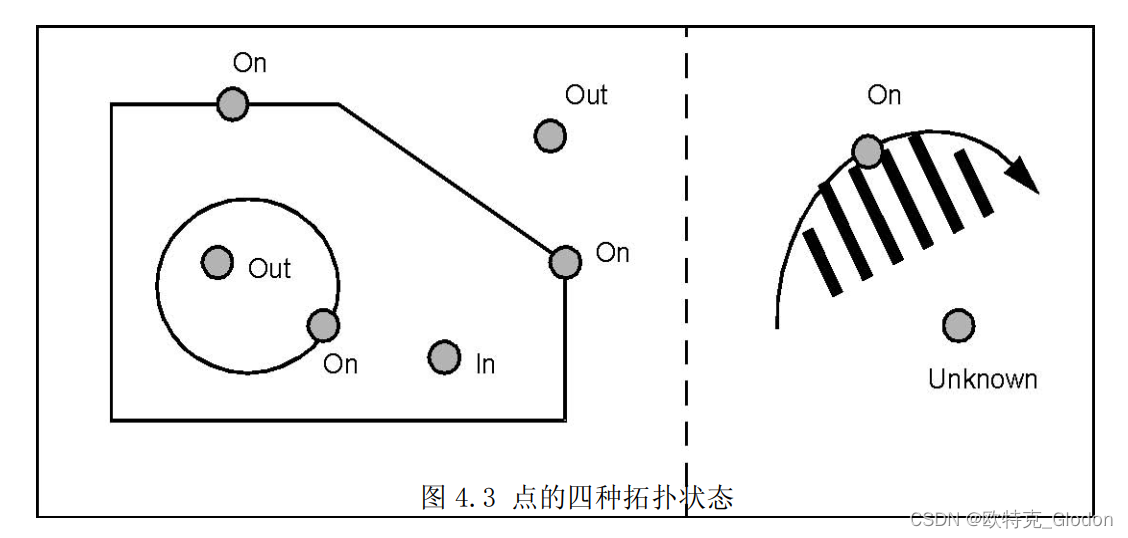
  UNKNOWN 术语之所以被引入，是因为这个枚举类经常被用于表达一个可能失败的计算结果。 当无法判断点在内部还是外部的时候（通常这种情况发生在线框或面是开放的时候），就可以用到该术语，如图 4.3 所示。

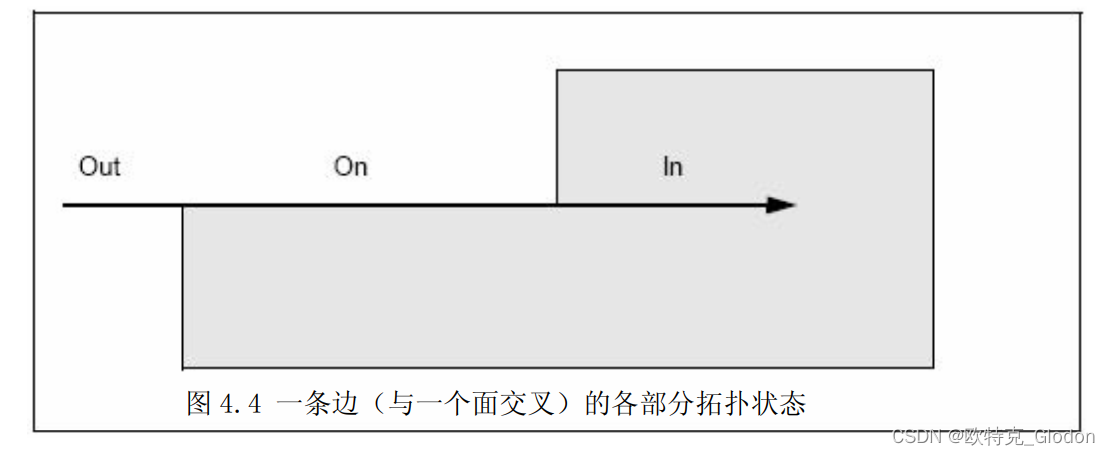
  State 枚举类也适用于对象的各个部分。 图 4.4 表示了一条边（与一个面交叉）的各部分拓扑状态。

3 三维几何数据结构

  三维几何对象的数据结构主要由 Geom 包提供。

  Geom 包包含了所有的基本几何转换（如等价、 旋转、 平移、 镜像、 缩放和复合变换等）。另外， Geom 包也提供了一些基于几何对象引用定义的特殊函数（如在 B 样条曲线上增加一个控制点，对曲线进行改善等）。

  Geom 包中所有几何实体都是以 STEP 方式处理的。包中可实现的非持久的通过句柄处理的对象有： 点、 笛卡尔点、 向量、 方向具有幅值的向量、 轴、 曲线、直线、 圆锥、 圆、 椭圆、 双曲线与抛物线、 基本曲面、 平面、 边界曲线与边界曲面、 裁剪曲线与裁剪曲面、 非均匀有理化 B 样条曲线与曲面、 Bezier 曲线与曲面、圆柱面、球面与螺旋面、扫描曲面、线性挤压曲面、旋转曲面、偏移曲面。

  对于每一条曲线（具有一个参数），其局部特征有：点、导数、正切、法向量、曲率和曲率中心。

  对于每一个参数， 曲面（具有两个参数） 的局部特征有： 导数、 切线、 曲率中心、 点、 法向量、 最大曲率、 最小曲率、 曲率的主方向、 中间曲率和高斯曲率。

  另外， GeomLProp 和 Geom2dLProp 包提供了一些描述算法的类，如表 4.7所示。

  TColGeom 为那些来自 Geom 包的曲线和曲面提供一维数组、 二维数组和序列的实现。 所有这些可实现的对象有两种处理方式： 通过引用处理和通过数值处理。