---

题目

链接: link

时间复杂度

概念

时间复杂度是一种函数，定量地描述了该算法运行的时间。既然是一种函数，就涉及到自变量与因变量。因变量代表是时间复杂的规模，自变量是时间复杂度的执行时间。这里的执行时间并不是秒，分钟这类的具体时间 ，它表示的是一种“执行次数”。要想计算时间复杂度首先得找到该算法中的循环，算法中循环执行的次数就是算法的时间复杂度 。

算法的时间复杂度的具体表示为：用大写的 O 来体现算法时间复杂度如O（f（n）），称之为 大 O 记数法。

时间复杂度的计算

注：可以理解为最坏情况下，算法的最高量级

一，单层for循环（线性阶）

判断一个数是偶数还是奇数，只需要求它除上 2 的余数是 0 还是 1，把所有数都判断一遍，并且对符合条件的情况进行计数，最后返回这个计数器就是答案，需要遍历所有的数，因此代码为：

int count(int n, int a[]) {
    int cnt = 0;
    for(int i = 0; i < n; ++i) {
        if(a[i] % 2)
            ++cnt;
    }
    return cnt;
}

我们可以发现这里的算法只有一层fo循环，执行过程中需要遍历n遍，所以这里的时间复杂度为O(n)。

---

二 ，多层for循环（指数阶）

int fun(int n)
{
   int cnt = 0;
  for(int i = 0;i < n;i++)
   {
     for(int j = 0; j<n; j++)
      {
        cnt++; 
      }
   }//两层循环，每次循环n次，因此为n*n
 
 
  for(int k = 0; k<n; k++)
   {
     ++cnt;
   }//一层循环，循环n次
  
  for(int l = 0;l<10;l++)
   {
     ++cnt;
   }//一层循环，循环10次
 
return cnt;
}

这里假如把所有的循环都算进去的话，时间复杂度就是O(nn+n+10)，但是我们并不能这样写。这是因为对于时间复杂度我们不需算出精确的数字，只需要算出这个算法属于什么量级即可。
所以在这里，为知道这个算法两级为多少，我们将字母n取为无穷大，这样10就无足轻重，然后时间复杂度就变成O(nn+n)，又因为nn远大于n，原式也可以表达成n(n+1)，即使-1也无关紧要，所以时间复杂度演变成O(n*n)。这就是大O渐近表示法，只是一种量级的估算，而不是准确的值。

---

三，冒泡排序（指数阶）

void bubblesort(int* a,int n)
{
   assert(a);
for(int end = n; end>0; end--)
    {
      int exchange = 0;
       for(int i = 1; i<end; i++)
           {
              if(a[i-1]>a[i])
              {
                swap(&a[i],&a[i-1]);
                 exchange = 1;
               }
            }
    
       if(exchange==0)
           break;
     }
}

在这里我们会发现这边不是简单的两层for循环，而是呈现一个等差数列，第一次循环第一次循环n-1次，第二次n-2次…一直到1，如果这样的话，难道时间复杂度就要写成O(n*(n+1)/2)了吗。
然而并不用，通过上面的例子我们看出，我们所采用大O渐近表示法去掉了对结果影响不大的项，并且在实际情况中一般只关注算法的最坏运行情况。
因此这里的算法复杂度只要把一些加法常数、保留最高项就行，例如在上述冒泡排序中,如果给定的数组就已经是有序的了,那么就是它的最好情况,时间复杂度为O(N).但是如果有非常多的数据很显然我们看不出它到底是否为最好情况,所以我们必须用最坏的期望来计算所以它是O(N*N).

---

四，指定常数循环（常数阶）

int fun(int n)
{
  int i = 0;int cnt = 0;
   for( i; i<100;i++)
     {
       cnt++;
      }
  return cnt;
}

此时时间复杂度为O(1)，这里的1不是指一次，而是常数次，该循环执行了100次，不管n多大，他都执行100次，所以是O(1)

---

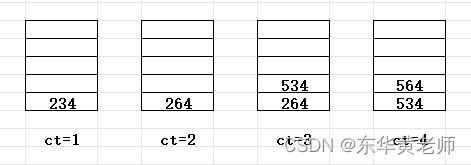
五，二分查找（对数阶）

int binary(int n, int a[], int k) 
{
	int left = 0, right = n - 1;
	while(l <= r) {
		mid = (l + r)/2;
		if(a[mid] == k) 
		    return mid;
		else if(a[mid] < k)
			right = mid + 1;
		else
			left = mid + 1;
	}
	return -1;
}

常见于二分查找中在有序数组中查找目标元素的算法。每次查找都将目标元素与数组中间的元素进行比较，如果相等则返回，如果目标元素小于中间元素，则在左半部分继续查找，否则在右半部分继续查找。每次查找都将搜索范围缩小一半
先找n/2，n/4，n/8一直到n等于1

因为这种算法，每多一次循环相当于，循环地覆盖范围变成了2^n，因此我们可以推出这个算法的时间复杂度为O($lo{g}_{2}x$)

---

由此我们可以得出结论

1.去除表达式中所有加法常数
2.修改的表达式中只保留最高阶项,因为只有它对最终结果产生影响
3.如果最高阶项系数存在且不是1,则将其系数变为1,得出最后的表达式
4.如果循环过程中只有常数时，，取常数次为时间复杂度

常见的时间复杂度

线性阶就像上面第一题一样，只有一层循环，时间复杂度随n的增大线性增加，函数在图像上表示为一条经过原点的直线,O(N)
指数阶指数阶一般是算法题的暴力解法，一般是多层循环的嵌套，例如上面题二中，最大是两层n次循环的嵌套，因此时间复杂度为O(N^2)，n的平方次
常数阶函数内循环为常数次或者没有循环，例如上面第四题，时间复杂度为O(1)
对数阶表示算法的时间复杂度与输入模 n 的对数成正比，其中对数的底数未指定，默认为2,10或e，根据具体情况而定。这意味着算法的运行随着输入规模的增加而增加但增长速度较慢。

---

解题思路

题目中要求我们把时间复杂度控制在O(log⁡n)里面，一般来说，这里的时间复杂度在没有设置底数的时候我们默认为10，这种算法随n增长较缓慢。

对于题目中找到最小的元素，我们第一个想到的就是最最暴力的冒泡排序，一个一个数遍历。

int findMin(int* nums, int numsSize) {
    int count = 1;
    for (int i = 0; i < numsSize; i++) {
        if (nums[i + 1] > nums[i])
            count++;
        else
            break;
    }
    return nums[count];
}

这种方法固然可行，但是此时的时间复杂度为O(n)，比O($lo{g}_{2}x$)大，对于算法复杂度的大小比较我们可以看成x随y的变换量，所以我们可以直观地知道这种粗暴的排序方法是不能够满足条件的，因此我们可以转变为二分查找，这种方法恰好符合题目所要求的时间复杂度

小tip：https://www.geogebra.org/download 是个很好的数学软件，可以画出函数等数学模型，更加直观便捷地感受数据

---

重新整理本题，一个不包含重复元素的升序数组在经过旋转之后，可以得到下面可视化的折线图

其中横轴表示数组元素的下标，纵轴表示数组元素的值。而图中标出了最小值的位置，就是我们需要查找的目标。

倘若使用二分查找的方法，我们就我们考虑数组中的最后一个元素 xxx：在最小值右侧的元素（不包括最后一个元素本身），它们的值一定都严格小于 xxx；而在最小值左侧的元素，它们的值一定都严格大于 xxx。因此，我们可以根据这一条性质，通过二分查找的方法找出最小值。

代码呈现

前者是基于left与right索引相同时出结果，即二分查找到数组只剩一个元素，然后直接输出left或right就行

int findMin(int* nums, int numsSize) {
    int left = 0;
    int right = numsSize - 1;
    while(left < right)
    {
        int mid = (left + right) / 2;
        if (nums[mid] < nums[right])
            right = mid;
        else
            left = mid + 1;
    }
    return nums[left];//因为此时left与right的索引一致
}