适用平台：Matlab+Yalmip+Cplex/Gurobi/Mosek

程序提出一种多源协同的两阶段配电网韧性提升策略。在灾前考虑光伏出力不确定性与网络重构，以移动储能配置成本与负荷削减风险成本最小为目标对储能的配置数量与位置进行预布局；在灾后通过多源协同运行与移动储能的动态调度最小化负荷削减成本，以提升配电网韧性。。程序算例丰富、注释清晰、干货满满，可扩展性和创新性很高！下面对文章和程序做简要介绍！

程序创新点：

1）考虑电网与交通网耦合提出基于移动储能预布局与动态调度的配电网韧性提升策略，在灾前与灾后两阶段保障供电；

2）针对光伏出力不确定性，建立灾前预布局鲁棒优化模型，利用列约束生成算法迭代求解预布局方案；

3）考虑极端灾害对交通网通行时间的影响，建立灾后恢复的混合整数二阶锥规划模型，通过多源协同实现电能量在时空维度上的最优分配。

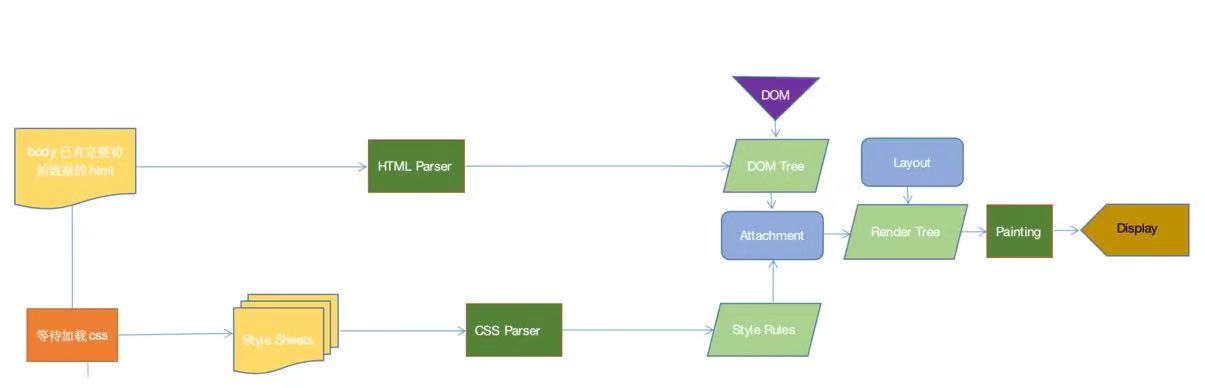
电网-交通网融合系统结构

考虑配电网内接入了光伏、移动储能、电动汽车充电桩（EVS）与柴油发电机等分布式资源，电网-交通网融合系统示意结构如下图所示。在灾害发生前配电网内负荷由上级主网供电，灾害发生后配电网失去主网供电且出现若干条线路故障，交通网络在灾害负荷恢复期间的实时通行能力受到灾害影响。

两阶段配电网韧性提升策略

在灾前预防阶段，考虑光伏极端出力场景与网络重构，在灾害发生时刻与持续时间未知的前提下，对移动储能的配置数量与位置进行预布局，确保移动储能在灾害发生后快速响应并参与负荷恢复；在灾后恢复阶段建立多源协同的灾后恢复优化模型，通过调度移动储能、电动汽车等资源实现电能在时空上的优化分配，以最大限度恢复重要负荷供电，提升配电网韧性，最后，可通过抢修故障设备将系统恢复至正常运行，不考虑线路抢修等设施重建措施。

灾前预布局鲁棒优化模型

以最恶劣光伏出力场景下的移动储能配置成本与负荷削减成本最小为目标，建立两阶段鲁棒优化模型来确定移动储能的配置数量与位置。第一阶段的决策变量为移动储能与节点的连接状态以及线路开关状态，第二阶段的决策变量为负荷削减功率、分布式电源出力、节点电压、支路功率与电流，光伏出力为不确定变量，目标函数如下：

采用盒式不确定集合来刻画新能源出力的不确定性

约束条件：

1）移动储能资源约束。2）配电网辐射拓扑约束。

3）负荷削减约束。4）分布式电源出力约束。

5）配电网运行约束。

多源协同的灾后恢复优化模型

在灾害发生后，配电网失去主网供电，设故障的持续时间可根据灾害强度和抢修资源数量做出预测。以故障持续时间内负荷削减功率加权值最小为目标，建立多源协同的灾后恢复优化模型，通过动态调度移动储能、电动汽车与柴油发电机，最大限度提升配电网韧性，目标函数如下：

约束条件:

1）移动储能的时空动态调度约束。2）电动汽车充放电约束

3）在灾后恢复阶段，各时刻的负荷削减功率、分布式电源出力与配电网运行仍需要满足相应约束，约束条件形式与灾前预布局阶段相同。

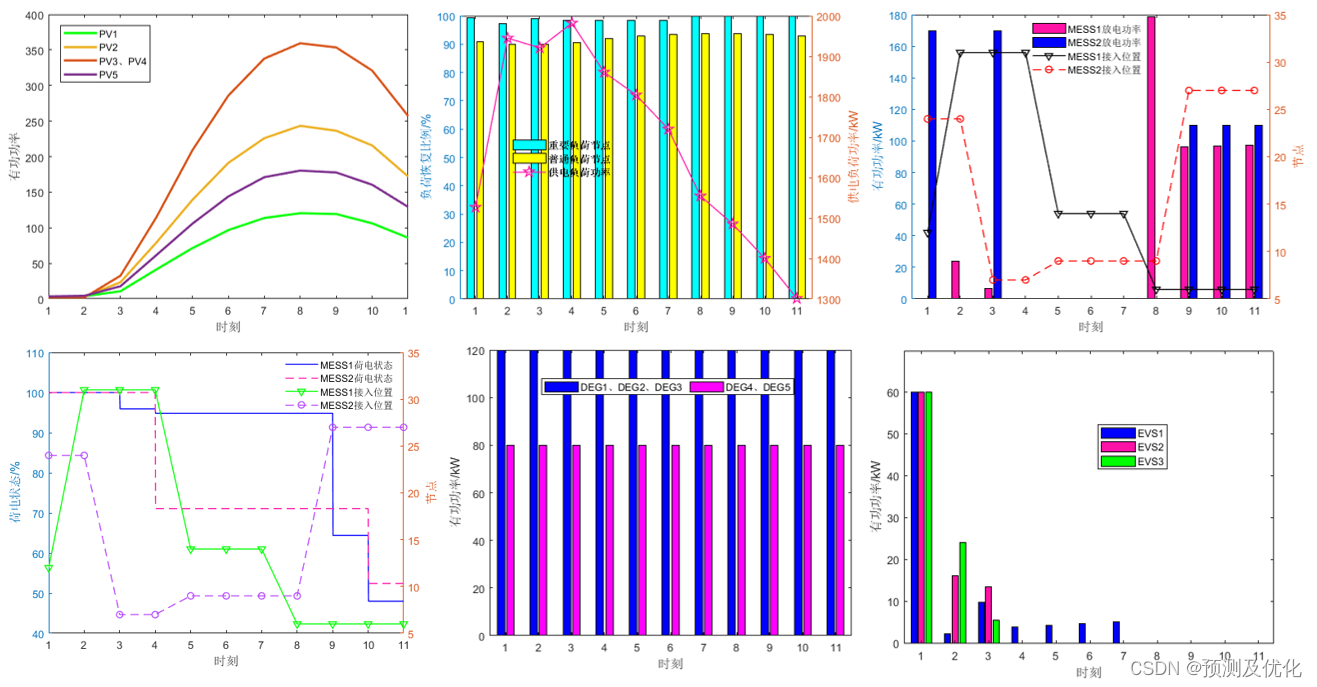
程序结果：

灾前优化程序采用Cplex/Gurobi求解器均可​！

灾后优化程序采用Cplex求解时间较长，建议采用Gurobi/Mosek求解器求解​！

---

部分程序：

%% 约束条件​
% 式25​Constraints = [Constraints , alpha_ME1(:,1) + alpha_ME2(:,1) == alpha_ME0];
% 式26​Constraints = [Constraints , alpha_ME1(j_index,t) + alpha_ME1(k_index,t+dt) <= 1 , alpha_ME2(j_index,t) + alpha_ME2(k_index,t+dt) <= 1];
% 式27​Constraints = [Constraints , sum(alpha_ME1(:,t)) <= 1 , sum(alpha_ME2(:,t)) <= 1];  
% 式28→35​Constraints = [Constraints , U_Mch(1,t) + U_Mdch(1,t) <= sum(alpha_MCS1(:,t)) , U_Mch(2,t) + U_Mdch(2,t) <= sum(alpha_MCS2(:,t))];
​% 式33、39Constraints = [Constraints , E_ME(:,t) == E_ME_max/SB , E_E(:,t) == E_E_max/SB];
% 式29-30Constraints = [Constraints , 0 <= P_Mch , P_Mch <= U_Mch*P_M_max/SB , 0 <= P_Mdch , P_Mdch <= U_Mdch*P_M_max/SB];
% 式31-32Constraints = [Constraints , 0 <= Q_Mch , Q_Mch <= U_Mch*Q_M_max/SB , 0 <= Q_Mdch , Q_Mdch <= U_Mdch*Q_M_max/SB];
% 式34Constraints = [Constraints , E_ME_min/SB <= E_ME , E_ME <= E_ME_max/SB];
% 式36-37Constraints = [Constraints , 0 <= P_Ech , P_Ech <= U_Ech*P_E_max/SB , 0 <= P_Edch , P_Edch <= U_Edch*P_E_max/SB];
% 式38Constraints = [Constraints , U_Ech + U_Edch <= 1];
% 式40Constraints = [Constraints , E_E_min/SB <= E_E , E_E <= E_E_max/SB];
% 式4Constraints = [Constraints , sum(alpha_ij) == NB - sum(S_vs)];
% 式5Constraints = [Constraints , delta_i(k,:)*F_ij - gamma_i(k,:)*F_ij == 1 - F_vs(O_DG==k)];
% 式6Constraints = [Constraints , -M0*S_vs <= F_vs , F_vs <= M0*S_vs];
% 式7Constraints = [Constraints , -M0*alpha_ij <= F_ij , F_ij <= M0*alpha_ij];
% 式8Constraints = [Constraints , 0 <= P_Lsu , P_Lsu <= P_L_max/SB];
% 式9Constraints = [Constraints , Q_Lsu(1,:) == 0 , Q_Lsu(2:NB,:) == (Q_L_max(2:NB,:)./P_L_max(2:NB,:)).*P_Lsu(2:NB,:)];
% 式10Constraints = [Constraints , 0 <= P_DG , P_DG <= P_DG_max/SB];
% 式11Constraints = [Constraints , 0 <= Q_DG , Q_DG <= Q_DG_max/SB];
% 式12Constraints = [Constraints , P_DG*tan_max >= Q_DG , P_DG*tan_min <= Q_DG];
% 式13-14Constraints = [Constraints , 0 <= P_MESS1 , P_MESS1 <= alpha_MCS1*P_M_max/SB , P_MESS1 <= ones(NB,1)*(P_Mdch(1,:) - P_Mch(1,:)) , P_MESS1 >= -P_M_max/S_Mch(1,:))];

部分内容源自网络，侵权联系删除！

欢迎感兴趣的小伙伴关注并私信获取完整版代码，小编会不定期更新高质量的学习资料、文章和程序代码，为您的科研加油助力！