降维算法之主成分分析 (Principal Component Analysis, PCA)

注意：本文引用自专业人工智能社区Venus AI

1 算法解读：

什么是主成分分析（PCA）？

主成分分析是一种常用的降维方法。当我们处理的数据有很多特征（维度）时，为了更简单地理解数据，并减少计算复杂度，我们会希望减少数据的维度，但同时保留数据的主要特征。PCA就是帮助我们实现这一目标的工具。

PCA的目标是什么？

PCA的主要目标是找到原始数据中方差最大的方向（这些方向是互相正交的），并将数据投影到这些方向上，从而实现降维。方向上的方差越大，说明数据在这个方向上变化越大，携带的信息量也越丰富。我们看一个使用PCA将二维数据降至一维的例子，该例子的代码将在后续介绍。

Fig1

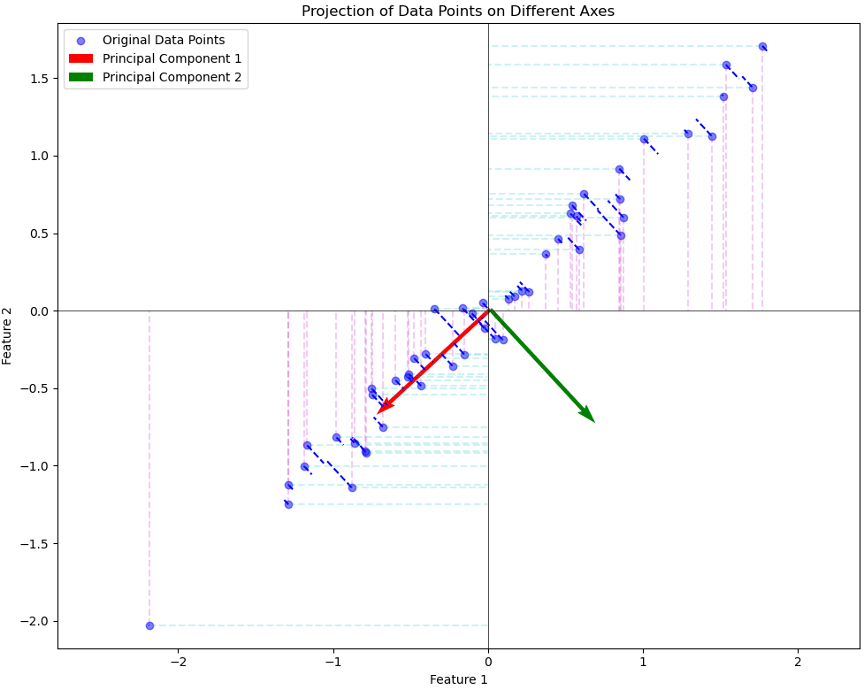
在上图中，我们展示了原始数据点在不同方向上的投影：

蓝色点：原始的二维数据点。

红色箭头：计算出的第一主成分方向。

绿色箭头：计算出的第二主成分方向

黑色虚线：原始数据点在第一主成分方向上的投影。

红色虚线：原始数据点在x轴（Feature 1轴）上的投影。

青色虚线：原始数据点在y轴（Feature 2轴）上的投影。

从图中可以观察到：

当数据点投影到x轴或y轴时，有很多点在投影后重叠，这导致了信息的丢失。相比之下，当数据点投影到第一主成分方向时，它们之间的距离得到了较好的保留，从而减少了信息的丢失。

这说明，与直接在某一坐标轴上进行投影相比，PCA通过寻找数据方差最大的方向进行投影，能更好地保留原始数据的结构，减少信息损失。PCA的目的就是计算得到红绿箭头这样的正交基，进行高维数据的投影降维。

2 步骤和细节：

a. 中心化：

为了简化计算，并使得主成分在原点附近，我们首先要对数据进行中心化处理。这一步包括计算每个特征的均值，并用每个特征值减去对应特征的均值。

b. 计算协方差矩阵：

协方差矩阵是一个描述特征之间相关性的矩阵。协方差越大，说明两个特征越相关。计算协方差矩阵的方式是用中心化后的数据点的特征值乘以其转置，然后除以数据点的数量。

c. 求特征值和特征向量：

下一步是计算协方差矩阵的特征值和特征向量。这一步通常会使用数学工具如NumPy库来完成。特征向量表示了主成分的方向，而特征值则表示了数据在这个方向上的方差大小。为了找到方差最大的方向，我们会对特征值进行排序。

d. 选择主成分：

一旦我们得到了所有的特征值和特征向量，我们就可以选择前k个最大的特征值对应的特征向量作为主成分。这k个特征向量构成了一个投影矩阵，我们会用这个矩阵来将原始数据投影到新的k维空间。

e. 降维：

最后一步是实际的降维操作。我们使用前面得到的投影矩阵将中心化后的原始数据投影到新的k维空间。这样，原始数据就被表示为了新空间中的点，而这个新空间的维度要小于原始空间。

3 PCA与SVD的联系：

相同之处：

PCA可以通过SVD来实现。具体而言，对于给定的数据矩阵X，我们可以计算其SVD分解，得到 $U\sum V^{T}$ 。其中，矩阵V的列向量（右奇异向量）就对应于PCA中协方差矩阵的特征向量，而奇异值的平方则对应于特征值。因此，我们可以通过SVD直接获得PCA的主成分，从而进行降维。

不同之处：

虽然PCA可以通过SVD实现，但本质上，它们是不同的数学技术。PCA是一种降维方法，关注数据的方差和协方差结构；而SVD是一种矩阵分解方法，可以应用于任意矩阵，不仅仅局限于协方差矩阵。

PCA需要先对数据进行中心化，而SVD不需要这一步骤。

PCA通常用于解释方差，找到数据的主要特征方向；SVD则更多地用于矩阵近似和解决线性方程组等问题。

简而言之，PCA和SVD在某些方面是相似的，特别是SVD可以用来计算PCA，但它们也有各自的特性和应用领域。

4 PCA示例

我们有一个包含五个四维数据点的数据集，可以表示为：

$\left.X=\left[\begin{array}{cccc}1&2&3&4\\4&3&2&1\\2&3&4&5\\5&4&3&2\\3&4&5&6\end{array}\right.\right]$

现在我们逐步进行计算：

步骤1: 中心化

1.1 计算每个特征的平均值

– 对于每一列 (特征) 计算平均值:

$\mathrm{mean}_j=\frac15\sum_{i=1}^5X_{ij}$

其中， $mean_j$ 是第 j 列的平均值， $X_{ij}$ 是矩阵 X 中第 i 行第 j 列的元素。

– 计算得到的每个特征的平均值为: [3.0,3.2,3.4,3.6]

1.2 中心化数据

– 用每个元素减去对应特征的均值:

$X_{\text{centered },ij}=X_{ij}-\text{ mean }_j$

– 中心化后的数据为:

$\left.\left[\begin{array}{cccc}-2.0&-1.2&-0.4&0.4\\1.0&-0.2&-1.4&-2.6\\-1.0&-0.2&0.6&1.4\\2.0&0.8&-0.4&-1.6\\0.0&0.8&1.6&2.4\end{array}\right.\right]$

步骤2: 计算协方差矩阵

– 使用中心化后的数据计算协方差矩阵: $Cov_{jk}=\frac14\sum_{i=1}^5X_{centered,ij}X_{centered,ik}$ 其中， $Cov_{jk}$ 是协方差矩阵的第 j 行第 k 列元素。

– 计算得到的协方差矩阵为:

$\left.\left[\begin{array}{cccc}2.5&1.0&-0.5&-2.0\\1.0&0.7&0.4&0.1\\-0.5&0.4&1.3&2.2\\-2.0&0.1&2.2&4.3\end{array}\right.\right]$

步骤3: 求协方差矩阵的特征值和特征向量

1. 计算特征值和特征向量:

对协方差矩阵进行特征值分解，得到特征值和对应的特征向量:

$\mathrm{Cov}\left(X_{\text{centered }}\right)v=\lambda v$

其中， λ 是特征值， v 是对应的特征向量。

2. 排序特征值并选择主成分:

将特征值进行降序排序，并选择前两个最大的特征值对应的特征向量作为主成分。

– 计算得到的特征值为:

$\begin{bmatrix}6.49,&2.31,&8.86\times10^{-17},&-2.97\times10^{-16}\end{bmatrix}$

– 对应的特征向量为:

$\begin{bmatrix}-0.45947273&-0.69920298&-0.48060841&0.26270811\\-0.03920365&-0.54631774&0.83662228&0.00794688\\0.38106544&-0.3934325&-0.23141933&-0.80401809\\0.80133452&-0.24054726&-0.12459454&0.5333631\end{bmatrix}$

– 选择了最大的两个特征值对应的特征向量作为主成分，它们分别为:

$\begin{bmatrix}-0.45947273&-0.69920298\\-0.03920365&-0.54631774\\0.38106544&-0.3934325\\0.80133452&-0.24054726\end{bmatrix}$

步骤4: 降维

– 使用选定的主成分将中心化后的原始数据投影到新的二维空间。这可以通过矩阵乘法来实现:

$X_{\mathrm{PCA}}=X_{\mathrm{centered}}\cdot V$

其中， V 是由选定的特征向量组成的矩阵。

降维后的数据为:

$\begin{bmatrix}1.13409747&2.11514135\\-3.06859337&0.58628893\\1.81782105&0.23564087\\-2.38486979&-1.29321155\\2.50154464&-1.64385961\end{bmatrix}$

这些值是新二维空间中的坐标值，分别对应原始四维空间中的五个数据点在两个主成分方向上的投影。

至此，我们完成了从四维降至二维的PCA的全部计算步骤。希望这个详细的例子能帮助你更好地理解PCA的原理和计算过程。

5 代码示例

为了直观地解释PCA的作用，我们将通过一个二维数据集的例子，演示如何使用PCA将其降至一维。

import  numpy as np
# 生成一个二维数据集
np.random.seed(0)
X = np.dot(np.random.rand(2, 2), np.random.randn(2, 50)).T
# 计算PCA
mean_X = np.mean(X, axis=0)
X_centered = X - mean_X
cov_matrix = np.cov(X_centered, rowvar=False)
eigvals, eigvecs = np.linalg.eigh(cov_matrix)
top_eigvec = eigvecs[:, np.argmax(eigvals)]
# 计算投影数据点
X_projected = np.dot(X_centered, top_eigvec.reshape(-1, 1))
# 计算第二主成分方向（由于在二维空间，第二主成分是第一主成分的正交方向）
second_eigvec = np.array([-top_eigvec[1], top_eigvec[0]])
下面，我们对上述PCA的结果进行绘图可视化，代码如下。
# 创建绘图对象
plt.figure(figsize=(10, 8))
# 绘制原始数据点
plt.scatter(X[:, 0], X[:, 1], alpha=0.5, color='blue', label='Original Data Points')
# 绘制主成分方向
plt.quiver(mean_X[0], mean_X[1], top_eigvec[0], top_eigvec[1],
           angles='xy', scale_units='xy', scale=1, color='red', width=0.005, label='Principal Component 1')
plt.quiver(mean_X[0], mean_X[1], second_eigvec[0], second_eigvec[1],
           angles='xy', scale_units='xy', scale=1, color='green', width=0.005, label='Principal Component 2')
# 绘制数据点在主成分方向上的投影
for i in range(X.shape[0]):
    plt.plot([X[i, 0], mean_X[0] + X_projected[i, 0] * top_eigvec[0]],
             [X[i, 1], mean_X[1] + X_projected[i, 0] * top_eigvec[1]], 'b--', alpha=1.0)
# 绘制数据点在x轴上的投影
for i in range(X.shape[0]):
    plt.plot([X[i, 0], X[i, 0]], [X[i, 1], 0], 'm--', alpha=0.2)
# 绘制数据点在y轴上的投影
for i in range(X.shape[0]):
    plt.plot([X[i, 0], 0], [X[i, 1], X[i, 1]], 'c--', alpha=0.2)
# 设置坐标轴标签和图例
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Projection of Data Points on Different Axes')
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.legend()
# 显示图像
plt.axis('equal')
plt.tight_layout()
plt.show(）

6 算法评价：

PCA（主成分分析）是一种常用的降维方法，它有一些显著的优点，但也存在一些局限性。下面是PCA算法的一些优缺点：

优点：

方差保留：PCA试图保留数据集中的最大方差，这有助于保留数据的主要特征和结构。
降噪：PCA可以将数据投影到主成分构成的低维空间，这有助于消除噪声和冗余特征。
可视化：通过降低数据的维度，PCA可以帮助我们将高维数据可视化，从而更好地理解数据的结构和关系。
计算效率：PCA的计算效率较高，特别是当使用SVD（奇异值分解）方法时，它可以高效地处理大规模数据集。

缺点：

线性假设：PCA假定数据的主成分是线性的，这意味着它可能不适合处理具有非线性结构的数据。
方差与重要性：PCA倾向于保留方差大的成分，但这并不总是与数据中的重要特征相对应。有时，方差小的成分可能包含了重要的信息。
正交性假设：PCA假定不同主成分之间是正交的，这在某些情况下可能不符合实际情况。
敏感性：PCA对数据的缩放和单位敏感，不同的缩放可能会导致不同的结果。因此，在应用PCA之前，通常需要对数据进行标准化。
解释性：PCA产生的主成分可能难以解释，因为它们通常是原始特征的线性组合，而这些组合可能缺乏实际意义。

总之，虽然PCA是一种强大且广泛应用的降维方法，但在使用时也需要考虑其局限性，并根据具体应用的需求和数据的特性进行选择。

7 算法变体：

Kernel PCA：使用核技巧处理非线性数据。当然，Kernel PCA (Kernel Principal Component Analysis) 是一个非常有用的降维技术，特别是当数据是非线性的。它通过将数据映射到一个高维特征空间，然后在该空间中应用传统的PCA，来处理非线性数据。核技巧（Kernel trick）可以让我们在原始空间中隐式地计算这种高维空间的特性，而无需真正执行映射。这个技巧我们将在SVM机器学习算法中进行展开介绍，

（也可以参考文献：1. Bishop, C. M. (2006). Pattern Recognition and Machine Learning. Springer.

2. Schölkopf, B., & Smola, A. J. (2002). Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond. MIT Press.）

PCA是一种强大且直观的降维方法，尽管它基于线性假设，但在许多应用中仍然非常有效。PCA可以有效地简化数据结构，使得后续分析和可视化更为方便。