A. Too Min Too Max(Problem - A - Codeforces)
题目大意:给定一个数组a[],从中找到4个下标i,j,k,l,求|ai-aj|+|aj-ak|+|ak-al|+|al-ai|的最大值。
思路:显然随便找四个下标与顺序无关,那么我们可以先将a[]排序。那么实际算的最大区间就如下:
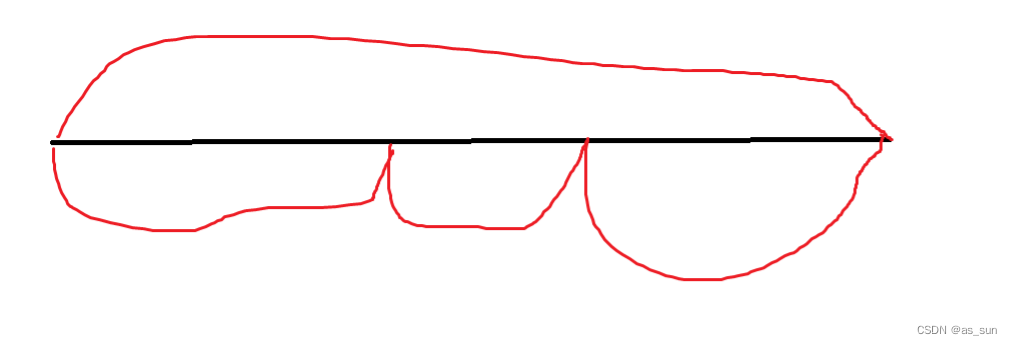
似乎就是二倍的极差。
但是我们需要注意到一点,每个元素不只有一个 ,例如1,1,2,2,3,如果算2倍极差的话,结果就是4,但是很显然不是:
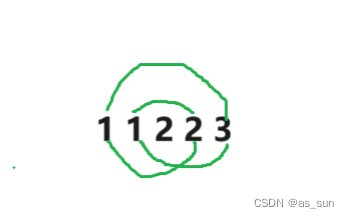
如图,我们找到这四个区间,得到的结果就是6.
所以实际要找的是最大的两个数和最小的两个数进行组合。
#include<bits/stdc++.h>
using namespace std;
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int n;
scanf("%d",&n);
int mi1=1e6+10,mi2=1e6+10,mx1=-1e6-10,mx2=-1e6-10;
for(int i=1;i<=n;i++)
{
int x;
scanf("%d",&x);
if(x>mx1) mx2=mx1,mx1=x;
else if(x>mx2) mx2=x;
if(x<mi1) mi2=mi1,mi1=x;
else if(x<mi2) mi2=x;
}
long long ans=(long long)mx1-mi1+(long long)mx1-mi2+(long long)mx2-mi1+(long long)mx2-mi2;
printf("%lld\n",ans);
}
}B. Yet Another Coin Problem(Problem - B - Codeforces)
题目大意:现在有5类硬币,面值分别为1,3,6,10,15,要求用最少数量的硬币凑出m,输出最少硬币的数量。
思路:很明显是一道dp问题,但是最开始真的没什么头绪,因为dp一般常问的是能否凑出m或者有多少种方案可以凑出m,这里问的却是最少硬币的数量。这题实际上还是比较巧妙的,有一个在背包问题的货币系统那题中出现过的思想——替代。显然3个1可以被1个3取代,2个3可以被1个6取代,3个6可以被1个15和1个3取代,3个10可以被2个15取代。所以实际上出了15,每个数出现的次数都有一个上限。那么我们实际上可以通过暴力枚举来解决。
#include<bits/stdc++.h>
using namespace std;
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int n;
scanf("%d",&n);
int ans=n;
for(int a=0;a<=2;a++)
{
for(int b=0;b<=1;b++)
{
for(int c=0;c<=3;c++)
{
for(int d=0;d<=2;d++)
{
int res=a*1+b*3+c*6+d*10;
if(res<=n&&(n-res)%15==0)
{
ans = min(a+b+c+d+(n-res)/15,ans);
}
}
}
}
}
printf("%d\n",ans);
}
}C. Find a Mine(Problem - C - Codeforces)
题目大意:这是一道交互题,给定一个n行m列的矩阵,矩阵中有两个地雷,位置分别是(x1,y1),(x2,y2),我们可以进行最多四次查询,每次查询一个(x,y),然后返回min(|x1-x|+|y1-y|,|x2-x|+|y2-y|),我们最终需要输出一个确定有地雷的位置。
思路:交互题的交互实际上并不重要,最重要的是如何确定策略。显然我们询问(1,1)后得到的曼哈顿距离对应的点是一条斜线,然后我最开始想的是去询问这条斜线的右上点,然后与这条斜线的交点一定是有地雷的,但是我忽略一种情况:
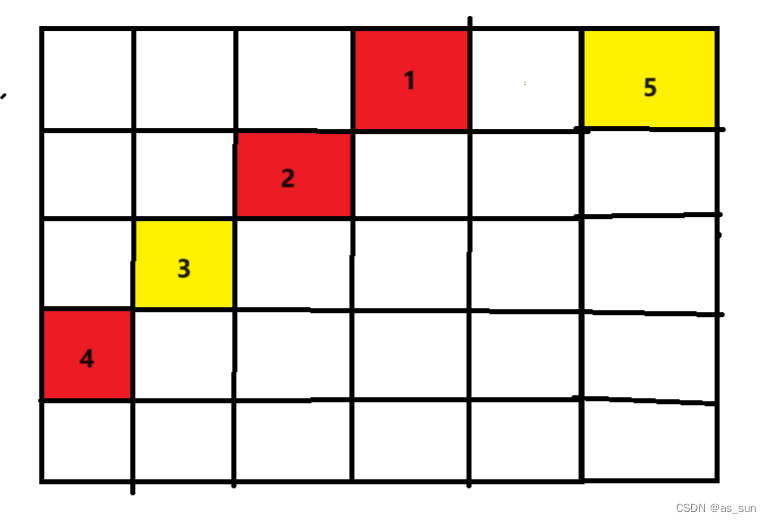
我们在询问(1,1)可以推出的候选位置是1,2,3,4,然后询问1得到d=2,那么与斜线相交的位置在2,但是实际上查到的d是由于5而产生的。所以只查一侧是不够的,实际上我们可以从右上和左下两个位置进行查询,总有一个是,不可能两都在斜线外。
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
int query(int x,int y)
{
printf("? %d %d\n",x,y);
fflush(stdout);
int c;
scanf("%d",&c);
return c;
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int n,m;
scanf("%d%d",&n,&m);
int c=query(1,1);
int l=max(1,c+2-m);
int p=query(l,c+2-l);
int r=max(1,c+2-n);
int q=query(c+2-r,r);
if(query(l+p/2,c+2-l-p/2)==0)
{
printf("! %d %d\n",l+p/2,c+2-l-p/2);
fflush(stdout);
}
else
{
printf("! %d %d\n",c+2-r-q/2,r+q/2);
fflush(stdout);
}
}
}D1. XOR Break — Solo Version(Problem - D1 - Codeforces)
题目大意:现在有两个数n,m,我们需要进行若干次操作,每次操作选定一个x,x满足:x<n,n^x<n,然后使n=x或者n=n^x,问能否使n最后变成m,输出n的变化次数和每次变成的数。
思路:这里的操作是异或,所以我们从二进制的角度来考虑,显然只有两者二进制位不同的时候才需要改变,每一位上如果需要变,要么是0变1,要么是1变0,对于0变1,n实际上会变大,所以我们要找一个更高位1变0来和它同步变化,否则n^x>n,就不满足要求。所以我们可以先遍历它们二进制的每一位,然后标记一下每一位,如果是1变0,标记成1,如果是0变1标记成2,然后从小往大遍历,每次当一个标记为2的位需要改变的时候,我们就往前找到一个标记为1的位和它一起变,否则如果找不到就直接退出输出-1,如此便可解决。
#include<bits/stdc++.h>
using namespace std;
int sta[64];
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
long long n,m;
scanf("%lld%lld",&n,&m);
vector<long long>q;
q.push_back(n);
memset(sta,0,sizeof sta);
for(int i=61;i>=0;i--)
{
if((n>>i&1) == (m>>i&1)) continue;
else if((n>>i&1) && !(m>>i&1)) sta[i]=1;//1变0
else sta[i]=2;//0变1
}
int flag=1;
for(int i=0;i<=61;i++)
{
if(sta[i]==2)
{
int d=i;
long long x=0;
while(d<=61&&sta[d]!=1)
{
if(sta[d])x+=1ll<<d;
d++;
}
x += 1ll<<d;
if(d>61||x>n)
{
flag=0;
break;
}
q.push_back(n^x);
n ^= x;
i=d;
}
else if(sta[i]==1)
{
long long x=1ll<<i;
q.push_back(n^x);
n ^= x;
}
}
if(flag)
{
cout<<q.size()-1<<endl;
for(auto it:q) cout<<it<<" ";
cout<<endl;
}
else cout<<"-1"<<endl;
}
}总结:所以你看啊,每个人擅长的题目类型都是不一样的,b,c虽然简单,但是之前没有接触过并不擅长,咱们这次接触了去学不就好了,像d题虽然过的人比b,c少,但是你接触过得多,比较擅长,所以就写出来了。不要担心了,不断去写新的题目,去接触新的题目,不断扩展自己的能力范围不就好了,不要因为自己不擅长的部分伤心,不擅长的意义就是告诉自己要去学习。