从零开始学习深度学习库-2：反向传播

news2024/11/17 8:51:31

欢迎来到本系列的第二篇文章，我们将从头开始构建一个深度学习库。
本博客系列的代码可以在这个Github仓库中找到。

上一篇文章

在上一篇文章中（链接见这里），我们实现了线性层和常见的激活函数，并成功构建了神经网络的前向传递。
到目前为止，我们的模型只能进行预测，但没有能力训练和纠正其预测。这正是我们今天要讲解的内容，通过实现一个称为反向传播的过程。

反向传播的工作概述

当神经网络进行训练时，它会被给定一个包含输入及其对应输出的数据集。
网络会根据数据集的输入产生预测，并计算其预测与数据集中给出的真实输出之间的偏差（这称为损失）。
训练神经网络的目标是最小化这个损失。
在计算出损失后，网络的权重和偏差会以某种方式进行调整，以减少损失值。记住在上一篇文章中提到，权重和偏差是我们可调节的网络参数，用于计算网络输出。
这个过程会重复数次，希望每次重复时损失都会减少。每次重复被称为一个时代（epoch）。

损失函数

虽然有许多不同的损失函数，但在这篇文章中，我们只会关注均方误差函数。未来的文章中会讨论更多损失函数。
损失函数接收网络的原始错误（通过预测输出 - 实际输出计算得出）并产生一个关于错误严重程度的度量。
均方误差（MSE）接收错误向量，并返回向量中所有平方值的平均值。
例如…

Network output: [1, 2, 3]
Actual outputs: [3, 2, 1]
Error: [-2, 0, 2]
Loss: 2.6666666 ( ( (-2)**2 + (0)**2 + (2)**2 ) / 3 )

在计算平均值之前先对误差进行平方的原因是为了使误差向量中的负值与正值同等对待（因为负数的平方是正数）。
下面是我们的Python类，用于实现均方误差（MSE）…

#loss.py

import numpy as np

class MSE:
    def __call__(self, pred, y):
        self.error = pred - y
        return np.mean(self.error ** 2)

反向传播

反向传播是网络的训练过程。
神经网络训练的目标是最小化损失。
这可以被视为一个优化问题，其解决方案在很大程度上依赖于微积分——更具体地说，是微分。

计算梯度

反向传播的第一步是找到网络中所有权重和偏差相对于损失函数的梯度。
我们用一个例子来演示…
我们的小型示例网络由以下部分组成：

  1. 线性层
  2. Sigmoid层
    所以整个网络的输出计算如下：
  • x - 网络输入
  • w - 线性层的权重
  • b - 线性层的偏差
  • a - 线性层输出
  • pred - 网络输出 / Sigmoid输出

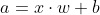
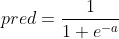
在这里插入图片描述
在这里插入图片描述
现在让我们计算损失

  • y - 对于输入 x 的期望输出
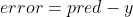
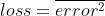
    在这里插入图片描述
    在这里插入图片描述
    现在我们需要找到相对于损失的权重/偏差的梯度。
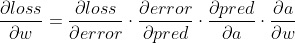
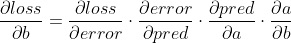
    在这里插入图片描述
    在这里插入图片描述
    这一步使用了链式法则。
    我们现在已经计算出了参数相对于损失的梯度。
    计算某一层相对于损失的权重/偏差梯度的一般规则是：
  1. 对每一层的输出相对于其输入进行微分（从最后一层开始，直到达到你想要调整参数的那一层）
  2. 将所有这些结果相乘，称之为 grad
  3. 一旦到达所需的层，对其输出相对于其权重进行微分（称这个为 w_grad），并对其偏差进行微分（称这个为 b_grad）。
  4. 将 w_grad 和 grad 相乘以获得相对于该层权重的损失梯度。对 b_grad 做同样的操作，以获得相对于该层偏差的损失梯度。

有了这个思路，下面是我们所有层和MSE的代码。

#loss.py

import numpy as np

class MSE:
    def __call__(self, pred, y):
        self.error = pred - y
        return np.mean(self.error ** 2)

    def backward(self):
        return 2 * (1 / self.error.shape[-1]) * self.error 

#layers.py

import numpy as np


class Activation:
    def __init__(self):
        pass

class Layer:
    def __init__(self):
        pass

class Model: 
    def __init__(self, layers):
        self.layers = layers

    def __call__(self, x):
        output = x
        for layer in self.layers:
            output = layer(output)

        return output

class Linear(Layer):
    def __init__(self, units):
        self.units = units
        self.initialized = False

    def __call__(self, x):
        self.input = x
        if not self.initialized:
            self.w = np.random.rand(self.input.shape[-1], self.units)
            self.b = np.random.rand(self.units)
            self.initialized = True

        return self.input @ self.w + self.b

    def backward(self, grad):
        self.w_gradient = self.input.T @ grad
        self.b_gradient = np.sum(grad, axis=0)
        return grad @ self.w.T

class Sigmoid(Activation):
    def __call__(self, x):
        self.output = 1 / (1 + np.exp(-x))

        return self.output

    def backward(self, grad):
        return grad * (self.output * (1 - self.output))

class Relu(Activation):
    def __call__(self, x):
        self.output = np.maximum(0, x)   
        return self.output

    def backward(self, grad):
        return grad * np.clip(self.output, 0, 1)

class Softmax(Activation):
    def __call__(self, x):
        exps = np.exp(x - np.max(x))
        self.output = exps / np.sum(exps, axis=1, keepdims=True)
        return self.output

    def backward(self, grad):
        m, n = self.output.shape
        p = self.output
        tensor1 = np.einsum('ij,ik->ijk', p, p)
        tensor2 = np.einsum('ij,jk->ijk', p, np.eye(n, n))
        dSoftmax = tensor2 - tensor1
        dz = np.einsum('ijk,ik->ij', dSoftmax, grad) 
        return dz

class Tanh(Activation):
    def __call__(self, x):
        self.output = np.tanh(x)

        return self.output

    def backward(self, grad):
        return grad * (1 - self.output ** 2)

每个类中的 backward 方法是一个函数，用于对层的输出相对于其输入进行微分。
随意查阅每个激活函数的导数，这将使代码更加易于理解。
线性层的 backward 函数不同，因为它不仅计算了输出相对于输入的梯度，还计算了相对于其参数的梯度。

注意
矩阵乘法的微分规则如下，其中 x 和 y 是被相乘的矩阵。
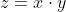
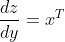
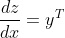
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

使用随机梯度下降优化参数

优化网络参数的方法有很多，但在这篇文章中，我们将介绍最基本的方法，即随机梯度下降（SGD）。
SGD非常简单。它将每个参数计算出的梯度乘以一个指定的学习率。然后，相应的参数减去这个结果。
使用学习率的原因是为了控制网络学习的速度。
最佳学习率值在少量的时代内最小化成本。
过小的学习率也能最小化成本，但需要经过多个时代，因此会花费时间。
过大的学习率会使损失逼近一个非最小值，因此网络无法正确训练。
下面是MSE的代码。

#optim.py

import layers
import tqdm
#Tqdm是一个进度条，所以我们可以看到代码运行的进度

class SGD:
    def __init__(self, lr = 0.01):
        self.lr = lr

    def __call__(self, model, loss):
        grad = loss.backward()

        for layer in tqdm.tqdm(model.layers[::-1]):
            grad = layer.backward(grad) #计算图层参数梯度

            if isinstance(layer, layers.Layer):
                layer.w -= layer.w_gradient * self.lr
                layer.b -= layer.b_gradient * self.lr

随着网络训练所需的一切都已准备就绪，我们可以在我们的模型中添加一个训练函数。

#layers.py

import numpy as np
import loss
import optim
np.random.seed(0)

#...

class Model: 
    def __init__(self, layers):
        self.layers = layers

    def __call__(self, x):
        output = x
        for layer in self.layers:
            output = layer(output)

        return output

    def train(self, x, y, optim = optim.SGD(), loss=loss.MSE(), epochs=10):
        for epoch in range(1, epochs + 1):
            pred = self.__call__(x)
            l = loss(pred, y)
            optim(self, loss)
            print (f"epoch {epoch} loss {l}")

#...

测试一下！

我们将构建并训练一个神经网络，使其能够作为异或门（XOR gate）。
异或门接收两个输入。输入可以是 0 或 1（代表假或真）。
如果两个输入相同，则门输出 0。
如果两个输入不同，则门输出 1。

#main.py

import layers
import loss
import optim
import numpy as np


x = np.array([[0, 1], [0, 0], [1, 1], [0, 1]])
y = np.array([[1],[0],[0], [1]]) 

net = layers.Model([
    layers.Linear(8),
    layers.Relu(),
    layers.Linear(4),
    layers.Sigmoid(),
    layers.Linear(1),
    layers.Sigmoid()
])

net.train(x, y, optim=optim.SGD(lr=0.6), loss=loss.MSE(), epochs=400)

print (net(x))

`` Output ... epoch 390 loss 0.0011290060124405485 100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s] epoch 391 loss 0.0011240809175767955 100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s] epoch 392 loss 0.0011191976855805586 100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s] epoch 393 loss 0.0011143557916784605 100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s] epoch 394 loss 0.0011095547197546522 100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s] epoch 395 loss 0.00110479396217416 100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s] epoch 396 loss 0.0011000730196106248 100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s] epoch 397 loss 0.0010953914008780786 100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s] epoch 398 loss 0.0010907486227668803 100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s] epoch 399 loss 0.0010861442098835058 100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s] epoch 400 loss 0.0010815776944942087 [[0.96955654] [0.03727081] [0.03264158] [0.96955654]] ``

正如您所见，结果非常好，与真实输出相差不远（0.001 的损失非常低）。
我们还可以调整模型，使其适用于其他激活函数。

#main.py

import layers
import loss
import optim
import numpy as np


x = np.array([[0, 1], [0, 0], [1, 1], [0, 1]])
y = np.array([[0, 1], [1, 0], [1, 0], [0, 1]]) 

net = layers.Model([
    layers.Linear(8),
    layers.Relu(),
    layers.Linear(4),
    layers.Sigmoid(),
    layers.Linear(2),
    layers.Softmax()
])

net.train(x, y, optim=optim.SGD(lr=0.6), loss=loss.MSE(), epochs=400)

print (net(x)) 

Output
epoch 390 loss 0.00045429759266240227
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s]
epoch 391 loss 0.0004524694487356741
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s]
epoch 392 loss 0.000450655387643655
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s]
epoch 393 loss 0.00044885525012255907
100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<00:00, 6236.88it/s]
epoch 394 loss 0.00044706887927775473
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s]
epoch 395 loss 0.0004452961205401462
100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<00:00, 5748.25it/s]
epoch 396 loss 0.0004435368216234964
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s]
epoch 397 loss 0.00044179083248269265
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s]
epoch 398 loss 0.00044005800527292425
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s]
epoch 399 loss 0.00043833819430972714
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s]
epoch 400 loss 0.0004366312560299245
[[0.01846441 0.98153559]
 [0.97508489 0.02491511]
 [0.97909267 0.02090733]
 [0.01846441 0.98153559]]

我们已经成功构建了一个有效的神经网络。这可以成功应用于更有用的事物，比如MNIST数据集，我们很快会在另一篇文章中使用它。
下一篇文章将介绍更多的损失函数和更多的优化函数。
感谢阅读！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1515406.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

使用Barrier共享鼠标键盘，通过macos控制ubuntu系统

使用Barrier共享鼠标键盘，通过macos控制ubuntu系统

之前文章写过如何使用barrrier通过windows系统控制ubuntu系统&#xff0c;该文章将详细介绍如何使用barrier通过macos系统控制ubuntu系统 一、macOS安装barrier macOS版本barrier链接 1、双击点开安装包 2、将安装包里的barrier拷贝到macOS的达达->应用程序中 3、在达达…
阅读更多...
2024考研计算机考研复试-每日重点（第二十期）

2024考研计算机考研复试-每日重点（第二十期）

公众号“准研计算机复试”&#xff0c;超全大佬复试资料&#xff0c;保姆级复试&#xff0c;80%的题目都是上岸大佬提供的。 研宝们&#xff0c;App更新啦&#xff01; 计算机组成原理&#xff1a; 10.☆什么是数据存储的大端模式和小端模式&#xff1f; 大端模式&#xff1a;数…
阅读更多...
防火墙基础理论(二)

防火墙基础理论(二)

漏洞扫描&#xff0c;设备联动 阻断未知威胁&#xff1a; 基于大数据统计 从运营角度管理设备 采集流量分析上报&#xff0c;探针
阅读更多...
零知识玩转AVH（5）—— 怎么玩（4）

零知识玩转AVH（5）—— 怎么玩（4）

接前一篇文章&#xff1a;零知识玩转AVH&#xff08;4&#xff09;—— 怎么玩&#xff08;3&#xff09; 上一回经过了一个艰苦的探索过程&#xff0c;最终完成了“arm-avh-best-practice-project-product-subscription-guide-cn.pdf”即“Arm虚拟硬件实践专题一&#xff1a;产…
阅读更多...
【Java系列】OOM 时，JVM 堆栈信息保存和分析

【Java系列】OOM 时，JVM 堆栈信息保存和分析

一、前言 在日常开发中&#xff0c;即使代码写得再谨慎&#xff0c;免不了还是会发生各种意外的事件&#xff0c;比如服务器内存突然飙高&#xff0c;又或者发生内存溢出(OOM)。当发生这种情况时&#xff0c;我们怎么去排查&#xff0c;怎么去分析原因呢&#xff1f; 一般遇到…
阅读更多...
OneDrive教育版迁移记录

OneDrive教育版迁移记录

背景 微软再次削减教育版优惠的OneDrive容量&#xff0c;从原先的5T直接砍到100G/人&#xff0c;同时对每个学校保留总共100TB的共享存储容量。 右键Onedrive图标——设置——存储容量可见 100GB对于重度用户显然是不够使用的&#xff0c;为此笔者改换Microsoft Office365家庭…
阅读更多...
javascript如何实现继承

javascript如何实现继承

文章目录 一、是什么二、实现方式原型链继承构造函数继承组合继承原型式继承寄生式继承寄生组合式继承 三、总结相关链接 一、是什么 继承&#xff08;inheritance&#xff09;是面向对象软件技术当中的一个概念。 如果一个类别B“继承自”另一个类别A&#xff0c;就把这个B称…
阅读更多...
基于SpringBoot+MYSQL+Vue的校园管理系统

基于SpringBoot+MYSQL+Vue的校园管理系统

目录 1、前言介绍 2、主要技术 3、系统流程分析 3.1、操作流程 3.2、添加信息流程 3.3、删除信息流程 4、系统设计 4.1 系统体系结构 4.2开发流程设计 4.3 数据库设计原则 4.4 数据表 5、运行截图(部分) 5.1管理员功能模块 5.2用户功能模块 5.3院校管理员功能模块…
阅读更多...
【django framework】ModelSerializer+GenericAPIView，如何在提交前修改某些字段值

【django framework】ModelSerializer+GenericAPIView，如何在提交前修改某些字段值

【django framework】ModelSerializerGenericAPIView&#xff0c;如何在提交前修改某些字段值 我们经常会遇到下面这种情况&#xff1a; 序列化器用的是ModelSerializer&#xff0c;写视图的时候继承的是generics.CreateAPIView。现在我想在正式提交到数据库(perform_create)之…
阅读更多...
使用Java自带的VisualVM监控远程服务器部署在Docker容器中的Java项目并使用Mat在线工具排查服务器内存泄露或内存溢出的原因

使用Java自带的VisualVM监控远程服务器部署在Docker容器中的Java项目并使用Mat在线工具排查服务器内存泄露或内存溢出的原因

事情是这样的&#xff0c;我们项目最近应业主的要求迁移到了新的服务器&#xff0c;起初一切正常&#xff0c;部署、上线、测试都没有问题&#xff0c;项目大概运行了一周的工作日时间都没出现问题&#xff0c;直到周六那天&#xff0c;项目经理打电话过来说服务器崩了&#xf…
阅读更多...
websocket逆向案例

websocket逆向案例

提示&#xff1a;文章写完后&#xff0c;目录可以自动生成&#xff0c;如何生成可参考右边的帮助文档 文章目录 前言一、案例地址二、分析流程三、逆向参数四、webSocket 交互位置总结 前言 本文章中所有内容仅供学习交流使用&#xff0c;不用于其他任何目的&#xff0c;不提供…
阅读更多...
第六篇【传奇开心果系列】Python的自动化办公库技术点案例示例：大学生数据全方位分析挖掘经典案例

第六篇【传奇开心果系列】Python的自动化办公库技术点案例示例：大学生数据全方位分析挖掘经典案例

传奇开心果博文系列 系列博文目录Python的自动化办公库技术点案例示例系列 博文目录前言一、Pandas库全方位分析挖掘大学生数据能力介绍二、大学生学生成绩数据分析数据挖掘示例代码三、大学生选课数据分析数据挖掘示例代码四、大学生活动参与数据分析数据挖掘示例代码五、大学…
阅读更多...
VsCode免密登录

VsCode免密登录

创建本地密匙 按下WinR输入cmd&#xff0c;输入 ssh-keygen -t rsa然后连续回车直到结束 找到Your public key has been saved in C:\Users\Administrator/.ssh/id_rsa.pub&#xff0c;每个人都不一样找到密匙所在地 打开id_rsa.pub这个文件&#xff0c;可以用记事本打开&am…
阅读更多...
Parade Series - WebRTC ( ＜ 300 ms Low Latency ) T.B.D

Parade Series - WebRTC ( ＜ 300 ms Low Latency ) T.B.D

Parade Series - FFMPEG (Stable X64) 延时测试秒表计时器 ini/config.ini [system] homeserver storestore\nvr.db versionV20240312001 verbosefalse[monitor] listrtsp00,rtsp01,rtsp02 timeout30000[rtsp00] schemartsp ip127.0.0.1 port8554 usr pwd context/cam08001…
阅读更多...
锐科达高速公路智慧隧道应急通讯网络广播解决方案

锐科达高速公路智慧隧道应急通讯网络广播解决方案

锐科达高速公路智慧隧道应急通讯网络广播解决方案 我国已是世界上公路隧道里程最长、规模最大、发展最快的国家。面对数量庞大的公路隧道&#xff0c;如何严防在隧道内发生重特大交通安全事故以及保障发生紧急情况下的应急通讯&#xff0c;是各地交通运输主管部门、各级指挥中心…
阅读更多...
在ubuntu20通过docker部署zabbix6

在ubuntu20通过docker部署zabbix6

部署Zabbix 6.x服务器在Ubuntu 20.04 LTS系统上使用Docker的方式可以简化安装过程并实现容器化管理。以下是一个简化的步骤指南&#xff1a; 步骤1&#xff1a;安装Docker和Docker Compose 确保你的Ubuntu系统已经安装了Docker和Docker Compose。如果没有&#xff0c;请执行以…
阅读更多...
创建SpringCloudGateWay

创建SpringCloudGateWay

创建SpringCloudGateWay 本案例基于尚硅谷《谷粒商城》项目&#xff0c;视频27 创建测试API网关 1、创建module 2、引入依赖 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:x…
阅读更多...
使用Nginx进行负载均衡

使用Nginx进行负载均衡

什么是负载均衡 Nginx是一个高性能的开源反向代理服务器&#xff0c;也可以用作负载均衡器。通过Nginx的负载均衡功能&#xff0c;可以将流量分发到多台后端服务器上&#xff0c;实现负载均衡&#xff0c;提高系统的性能、可用性和稳定性。 如下图所示&#xff1a; Nginx负…
阅读更多...
snowny-小诺框架-标签tabs消失不见

snowny-小诺框架-标签tabs消失不见

可能是由于&#xff0c;在配置菜单时&#xff0c;排序数字过小造成的&#xff0c;将排序数字改成大于0的数字就好使了。
阅读更多...
ChatGPT浪潮来袭！谁先掌握，谁将领先！

ChatGPT浪潮来袭！谁先掌握，谁将领先！

任正非在接受采访时说 今后职场上只有两种人&#xff0c; 一种是熟练使用AI的人&#xff0c; 另一种是创造AI工具的人。 虽然这个现实听起来有些夸张的残酷&#xff0c; 但这就是我们必须面对的事实 &#x1f4c6; 对于我们普通人来说&#xff0c;我们需要努力成为能够掌握…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023